Lỗ đen, lỗ sâu đục và cỗ máy thời gian (Phần 43)

Stephen Hawking phạm sai lầm

Không bao lâu sau khi tôi bắt đầu nghiên cứu tiến sĩ vào năm 1987, tôi vào thư viện trường đại học của mình làm cái việc gọi là tìm kiếm tài liệu. Tôi đang nghiên cứu một vấn đề vật lí có liên quan đến một phép tính toán học dài ngoằng mô tả cái xảy ra khi hai hạt nhân nguyên tử va chạm nhau, và tôi đang tìm một số tư liệu tham khảo trong các tập san khoa học liên quan đến nghiên cứu của tôi. Không thành công cho lắm trong việc tìm gặp một bài báo nhất định và có chút chán nản, tôi quyết định tìm kiếm bất kì bài báo khoa học nào của Stephen Hawking, chẳng vì lí do gì cả mà tôi cảm thấy nghiên cứu của ông về vũ trụ học có thể mang lại một chút thư giãn cho bản thân mình. Tôi tìm gặp một bài báo của ông hồi hai năm trước đó, năm 1985, trong đó ông trình bày chiều của thời gian có thể đảo như thế nào nếu như Vũ trụ đã từng bắt đầu co lại. Vấn đề nghe có vẻ hứa hẹn. Tôi đã photo một bản của bài báo và đọc nó trên đường ngồi tàu về nhà.

Tôi chăm chú theo dõi những lập luận của vài trang đầu nhưng rất mau chóng bị sa lầy với toán học. Tuy nhiên, tối hôm đó, tôi quả quyết rằng ông đã sai, nhưng vì tôi không thể theo dõi hết các chi tiết toán học nên tôi không cảm thấy có đủ cơ sở an toàn. Xét cho cùng, ông là một nhà khoa học nổi tiếng thế giới còn tôi chỉ mới khởi nghiệp nghiên cứu sinh trong một lĩnh vực nghiên cứu khác. Mặc dù tôi không biết vào lúc ấy Hawking đã nhận ra rằng những kết luận của ông trong bài báo đó, cái đã thu hút sự chú ý lớn, là sai lầm. Tuy vậy, tôi nói dông dài như thế chủ yếu để chứng minh thời gian có thể khó hiểu và viễn vông như thế nào nếu một người nào đó tầm cỡ như Stephen Hawking mà còn phạm sai lầm. Thật vậy, cái lôi cuốn tôi là nhìn xem có bao nhiêu nhà khoa học nổi tiếng và chuyên gia thế giới khác có thể giữ những quan điểm hoàn toàn trái ngược về cái gì đó cơ bản như thế này³. Tất cả là do sự lộn xộn mà nhiều người hiểu về khái niệm entropy. Trước tiên, tôi sẽ mô tả ngắn gọn tại sao Hawking đi tới kết luận gây tranh cãi của ông.

Định luật thứ hai nhiệt động lực học nên áp dụng mà không cần suy xét ở mọi nơi trong Vũ trụ phát biểu rằng entropy của một hệ cô lập bất kì không thể giảm đi. Vậy thì tại sao không nên áp dụng nó cho toàn bộ Vũ trụ? Xét cho cùng, Vũ trụ ở mức tổng thể của nó được định nghĩa là một hệ cô lập vì chẳng có cái gì ở bên ngoài nó cả. Thật vậy, entropy của toàn bộ Vũ trụ thật sự đang tăng lên và hàm nghĩa rằng nó phải có trật tự hơn so với trước đây. Thật vậy, nó phải có một entropy tối thiểu lúc Big Bang và rồi xả dây cót, hay tăng lên, kể từ đó.

Tất nhiên, bạn có thể xem việc chúng ta nói về entropy của Vũ trụ tổng thể là có phần tham vọng, nếu không nói là ngạo mạn, nhưng vì chúng ta đang cố gắng xác định kích cỡ, hình dạng của tuổi của nó, vậy thì tại sao không xác định entropy của nó luôn? Để bắt đầu, tôi sẽ xét một vũ trụ “mô hình” đơn giản có ít cái phải làm với thực tại nhưng sẽ giúp chúng ta tìm hiểu xem định luật thứ hai có thể giữ vai trò gì trong sự phát triển của Vũ trụ. Hãy tưởng tượng một cái hộp kín trong đó tất cả các phân tử không khí tập trung lại ở một góc. Một cách có được như vậy là nếu như toàn bộ không khí ban đầu được giữ bên trong một cái chai đặt tại góc đó rồi sau đó có thể mở nắp chai từ xa. Entropy của cái hộp ở trạng thái ban đầu này là thấp vì cái chứa bên trong ở trạng thái có trật tự cao với toàn bộ không khí được giữ chặt bên trong cái chai.

Khi thời gian trôi qua, không khí sẽ thoát ra khỏi cái chai và lan khắp cái hộp làm cho entropy của nó tăng lên. Khi các phân tử không khí phân bố đều trong khắp cái hộp thì entropy sẽ ở giá trị tối đa và hệ được nói là ở trạng thái cân bằng. Trường hợp này tương đương với một bộ bài tây hoàn toàn bị xáo trộn. Có một xác suất hết sức nhỏ rằng một lúc nào đó về sau chúng ta sẽ thấy toàn bộ các phân tử ở vào trong chai trở lại.

Giờ hãy tưởng tượng cái hộp lớn hơn nhiều (ví dụ bằng cỡ một thiên hà). Với quá nhiều phân tử bên trong cái hộp, khối lượng chung của chúng đủ cho lực hấp dẫn có sự tác dụng. Cái có thể xảy ra là một nhóm trong số chúng có thể bị trôi giạt ngẫu nhiên đến gần hơn khoảng cách trung bình. Một khi đều này xảy ra, chúng ta sẽ thấy lực hấp dẫn chiếm ưu thế và làm cho chúng bị hút về phía nhau. Càng có nhiều phân tử co cụm lại thì sức hút hấp dẫn chung của chúng lên các phân tử xung quanh sẽ càng lớn. Sự co cụm do hấp dẫn như thế này cuối cùng sẽ làm cho toàn bộ không khí tụ lại thành những đống có kích cỡ khác nhau trong toàn thể tích của cái hộp, với những khoảng không trống rỗng ở giữa chúng. Cái gì xảy ra với entropy lúc này? Chúng ta đã bắt đầu với những phân tử phân bố đều khắp thể tích và entropy ở giá trị tối đa và kết thúc ở cái trông tựa như một trạng thái có trật tự cao hơn, tựa như việc quét những chiếc lá mùa thu rơi gom thành từng đống. Trông có vẻ như lực hấp dẫn đã làm cho định luật thứ hai bị vi phạm.

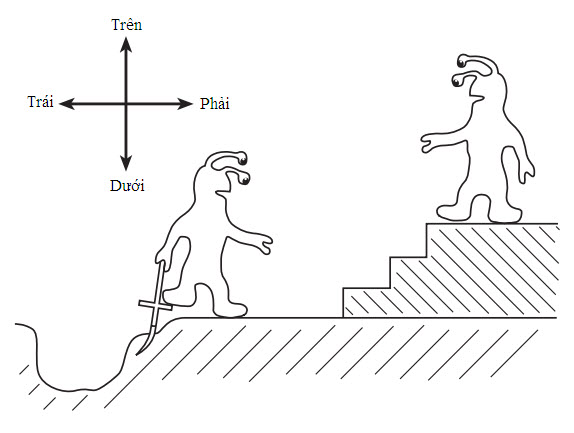
Không phải thế. Nếu bạn nghĩ sự tăng entropy là một quá trình đi tới kết thúc, thì vật chất ở đủ gần nhau để chịu lực hút hấp dẫn sẽ “xả dây cót” khi nó hút hấp dẫn với nhau. Một quả bóng nằm trên đỉnh đồi thì có entropy thấp. Khi nó lăn xuống đồi (do tác dụng của lực hấp dẫn), entropy của nó tăng. Chúng ta nói nó đang mất khả năng thực hiện công. Chúng ta đã học ở trường phổ thông rằng quả bóng nằm tại đỉnh đồi có thế năng chuyển hóa thành động năng khi nó lăn xuống. Theo kiểu tương tự như vậy, một món đồ chơi lên dây cót (cái tôi đã mô tả ở phần trước là có entropy thấp) có thế năng mất dần khi nó xả dây cót và entropy của nó tăng lên.

Như vậy, lực hấp dẫn làm tăng entropy, nhưng điều này vẫn không lí giải được làm thế nào entropy trong cái hộp tăng lên nếu ban đầu nó đã ở giá trị cực đại. Câu trả lời là suốt thời gian các phân tử cách đều nhau, lực hấp dẫn sẽ hút theo mọi chiều và triệt tiêu, và entropy ở giá trị cực đại. Nếu, do tình cờ (và cái gì cũng là có thể) các phân tử ở một vùng nhất định ở gần nhau hơn so với trung bình thì trạng thái này biểu diễn một sự lệch tạm thời khỏi trạng thái entropy cực đại (trạng thái cân bằng). Để cho định luật thứ hai áp dụng được cho tình huống trên, những phân tử này có hai chọn lựa: chúng có thể hoặc trôi giạt trở ra vị trí cân bằng ban đầu của chúng, hoặc chúng có thể hút hấp dẫn lên nhau tạo thành một cụm. Dù theo cách nào thì entropy cũng tăng trở lại giá trị cực đại. Cả hai kịch bản đều có thể xem là sự kết thúc của hệ, nhưng giờ chúng ta có hai bức tranh thay thế của trạng thái entropy cực đại.

Giờ ta đã sẵn sàng đương đầu với Vũ trụ thực. Hawking bắt đầu lập luận của ông bằng cách phát biểu rằng Vũ trụ phải có entropy tối thiểu lúc Big Bang và, vì nó phải tuân theo định luật thứ hai của nhiệt động lực học, đã xả dây cót từ đó, tiến về phía một trạng thái có entropy cực đại. Ông đã phát triển một lí thuyết của Vũ trụ đòi hỏi nó phải kín và tin rằng nó chứa đủ vật chất để một ngày nào đó làm dừng sự giãn nở và làm cho nó co lại trong một Vụ Co Lớn. Hãy nhớ ở Chương 3 rằng đây là một kịch bản có thể có cho số phận của Vũ trụ mà chúng ta không thể bác bỏ. Phần còn lại của chương này sẽ giả sử rằng đây thật sự là số phận của Vũ trụ (cái hiện nay là không có khả năng, như chúng ta đã biết).

Trong mô hình của Hawking, điểm kì dị Vụ Nổ Lớn và Vụ Co Lớn là giống hệt nhau. Nói chung, trong cả hai trường hợp, toàn bộ vật chất và năng lượng trong Vũ trụ sẽ bị nén đến mật độ vô hạn và kích cỡ zero. Như vậy, nếu điểm kì dị Vụ Nổ Lớn ở một trạng thái entropy thấp, thì điểm kì dị Vụ Co Lớn cũng thế. Vì thế, khi Vũ trụ co lại, entropy của nó sẽ giảm trở lại và định luật thứ hai của nhiệt động lực học sẽ bị vi phạm trong pha này. Hawking tin rằng trạng thái giãn nở cực đại cũng biểu diễn trạng thái entropy cực đại. Như vậy, pha co lại của Vũ trụ sẽ là sự đảo ngược thời gian của pha giãn nở.

Nói theo mũi tên thời gian, nếu entropy bắt đầu giảm trong pha co lại thì mũi tên nhiệt động lực học phải đảo chiều (vì nó được định nghĩa là luôn luôn hướng theo chiều entropy tăng) và nếu mũi tên chủ quan (triết lí) của chúng ta luôn luôn cùng chiều với mũi tên nhiệt động lực học, thì thời gian của chúng ta cũng sẽ trôi ngược. Điều này có nghĩa là thay vì Vụ Co Lớn là một sự kiện trong tương lai của chúng ta, thì nó sẽ là một sự kiện trong quá khứ. Tất nhiên, tôi đang giả sử con người sẽ sống sót trong hàng tỉ năm trời cần thiết để đưa giả thuyết này vào kiểm tra, nhưng nếu chúng ta làm như thế thật ra chúng ta sẽ không nhìn thấy Vũ trụ đang co lại. Vì thời gian của chúng ta đang trôi ngược nên chúng ta nghĩ Vũ trụ vẫn đang giãn nở. Do đó, chúng ta cũng sẽ không nhìn thấy bất cứ sự vi phạm nào của định luật thứ hai của nhiệt động lực học. Rốt cuộc, theo chúng ta, entropy sẽ đang tăng như bình thường. Kết luận thú vị nhất thu được từ tình huống kì lạ này là Vũ trụ hiện nay có lẽ đang co lại, và chỉ vì chúng ta có mũi tên thời gian hướng theo chiều entropy tăng nên chúng ta tin tưởng một cách sai lầm rằng nó đang giãn nở!

Lúc ấy tôi đã không nhận ra, nhưng quan điểm đảo chiều thời gian như thế này trong một Vũ trụ đang co lại thật ra là của Thomas Gold hồi thập niên 1960. Hawking đã thử đặt quan điểm này lên một cơ sở lí thuyết chắc chắn hơn bằng cách viện dẫn đến bản chất lượng tử của hai điểm kì dị. Thật vậy, hành trạng của Vũ trụ khi nó ở gần sự giãn nở tối đa sẽ phải rất lạ trong bức tranh ban đầu của Hawking. Giả sử có một người sống sót từ pha giãn nở qua pha co lại trong khi ở bên trong một phi thuyền vũ trụ khép kín. Mũi tên thời gian của cô ta sẽ bất ngờ đảo chiều và cô ta sẽ không nhớ thời điểm giãn nở cực đại vì lúc này nó nằm trong tương lai của cô ta.

Giờ tôi sẽ mô tả sự phản bác của tôi đối với quan điểm này. Trước hết, Hawking đã sử dụng các từ “giãn nở”, “co lại” và “sống sót qua thời kì giãn nở cực đại vào pha co lại”. Ngôn từ như thế hàm ý rằng phải có một mũi tên thời gian độc lập, bên ngoài, hướng từ Vụ Nổ Lớn đến Vụ Co Lớn. Nếu không sẽ chẳng có gì để phân biệt giữa hai hiện tượng và chúng ta không thể nói cái nào “có trước” cái nào. Khi khẳng định chúng ta có thể suy nghĩ “sai lầm” rằng chúng ta đang sống trong pha giãn nở nhưng “thật ra” đang ở trong pha co lại, chúng ta cần có một thời gian bên ngoài có tác dụng như một quan tòa và cho chúng ta biết Vũ trụ thật sự đang diễn biến ra sao. Chúng ta biết không có mũi tên nào như thế và việc đề xuất một thời gian có thể tồn tại như vậy làm nhớ lại phần trình bày trước đây của tôi về một thời gian giả thuyết bên ngoài chúng ta cần có để dựa trên đó đo tốc độ trôi của thời gian của chúng ta. Và nếu không có một chiều thời gian ưu tiên nào để đánh dấu pha giãn nở và co lại thì Vụ Co Lớn thật ra sẽ tương đương với Vụ Nổ Lớn và cũng sẽ đánh dấu sự bắt đầu của thời gian. Vì thế, chúng ta sẽ có thời gian trôi từ cả hai điểm kì dị, theo chiều ngược nhau, về phía “kết thúc của thời gian” lúc giãn nở cực đại.

Tôi muốn làm sáng tỏ vấn đề sự kết thúc của thời gian này bằng cách xét số phận của con người còn sống sót trong một phi thuyền vũ trụ ở gần thời điểm giãn nở cực đại. Cô ta tính được rằng Vũ trụ sẽ đạt tới sự giãn nở cực đại vào lúc ba giờ chiều hôm ấy (ta gọi đó là T-max). Cô ta nhận thức được rằng mũi tên thời gian của mình sắp đảo chiều. Lúc ba giờ kém một giây, mọi thứ vẫn bình thường và cô ta biết mình còn một giây nữa. Cái gì sẽ xảy ra hai giây sau đó? Lúc này là ba giờ quá một giây và chúng ta đang ở trong pha co lại. Nếu như mũi tên thời gian của cô ta lúc này đã đảo chiều và mọi quá trình bên trong phi thuyền vũ trụ đang chạy ngược thì đồng hồ của cô ta lúc này sẽ trở lại chỉ ba giờ kém một giây. Cô ta sẽ vẫn nghĩ rằng Vũ trụ hãy còn một giây giãn nở nữa.

Ngay cả lúc ba giờ kém một phần triệu giây ở phía bên này của T-max sẽ vẫn chẳng có gì xảy ra khác thường, nhưng hai phần triệu giây sau đó cô ta sẽ vẫn tin rằng T-max còn cách một phần triệu giây nữa. Chúng ta có thể tiến gần đến T-max như chúng ta muốn nhưng sẽ không bao giờ có một thời điểm sau đó nữa. Nó thật sự đánh dấu sự kết thúc của thời gian.

Những phản bác trên không chứng minh rằng Hawking là sai mà ngôn ngữ ông sử dụng đã giả sử trước một mũi tên thời gian nữa không đổi chiều lúc T-max, và không có cái gì để tham chiếu với nó cả.

Sau khi thảo luận lí thuyết của ông với các đồng nghiệp, Hawking sớm nhận ra rằng Vũ trụ không cần quay trở lại một trạng thái entropy thấp lúc Vụ Co Lớn và do đó sẽ không phải đảo chiều mũi tên thời gian của chúng ta. Entropy của Vũ trụ có thể tiếp tục tăng từ pha giãn nở qua pha co lại. Thật không may, Hawking đã bị mắc chứng liệt thần kinh vận động và không thể viết một bài báo đọc nhanh giải thích sai lầm của ông. Tôi nhớ như in lúc đọc quyển sách best-seller của ông Lược sử thời gian trong lúc ngồi trên xe lửa đi làm lúc một hai năm sau khi nó được xuất bản – một người bạn đã mua tặng tôi một quyển in bìa mềm tại sân bay New Delhi trước khi nó có mặt tại Anh quốc khá lâu – và tôi nhớ cái cảm giác vừa bất ngờ vừa khâm phục trước sự trung thực của Hawking. Tôi nhớ nhất là cái vẻ mặt ngượng nghịu cười ngu ngơ của mình đã thu hút sự chú ý của những hành khách khác trên xe.

Vậy thì làm thế nào chúng ta hiểu sự khác biệt giữa Vụ Nổ Lớn entropy thấp và Vụ Co Lớn entropy cao? Một lời giải thích là không gian ở gần hai điểm kì dị đó có dạng hình học khác nhau. Suy nghĩ hiện nay là các lỗ đen là những cái hồ chứa entropy. Chúng càng lớn thì entropy của chúng càng cao. Vì Vụ Co Lớn có thể xem là một lỗ đen tối hậu đã nuốt chửng toàn bộ Vũ trụ, nên nó phải có một entropy cực kì cao. Vụ Nổ Lớn, trái lại, giống với một lỗ trắng và sẽ có entropy rất thấp.

Tuy nhiên, lời giải thích này không thỏa đáng cho lắm. Rốt cuộc thì lực hấp dẫn từ đâu mà có? Sự giãn nở xảy ra trong cái gì? Và làm thế nào Vũ trụ ở trong một trạng thái entropy thấp như thế lúc ban đầu?

Thoạt nhìn, có vẻ như Vũ trụ lúc ấy ở trong một trạng thái entropy thấp. Các ngôi sao là những điểm nóng trong không gian phát xạ nhiệt của chúng vào môi trường xung quanh của chúng và làm cho entropy tăng lên (hãy nhớ quan điểm truyền nhiệt là một cách định nghĩa entropy). Khi một ngôi sao ngừng tỏa sáng, nó đã hoàn toàn cạn kiệt và sẽ ở trong một trạng thái entropy cao (cho dù nó có biến thành một lỗ đen hay không). Vì thế, sẽ có một thời điểm trong tương lai xa xôi khi tất cả các ngôi sao đã cháy hết và bức xạ của chúng sẽ phân bố đều khắp không gian (entropy cao). Tuy nhiên, ở đây có một trở ngại nghiêm trọng, cái các nhà vật lí đã vật vã chiến đấu với mức độ thành công khi nhiều khi ít. Trước khi các ngôi sao và thiên hà hình thành trong Vũ trụ sơ khai, Vũ trụ đã ở trong một trạng thái cân bằng nhiệt, với năng lượng của nó phân bố đều đến mức không có vùng không gian nào nóng hơn vùng không gian nào. Chắc chắn đây là một trạng thái entropy cực đại! Vậy thì cái gì làm cho các ngôi sao hình thành lúc ban đầu?

Có một đề xuất như thế này: Đúng là Vũ trụ đã bắt đầu ở một trạng thái entropy cực đại, nhưng khi đó nó cũng rất nhỏ. Entropy mà nó có là cực đại có thể có đối với vũ trụ kích cỡ đó. Sau đó Vũ trụ trải qua một thời kì giãn nở nhanh (lạm phát) và lượng entropy cực đại mà nó có thể có tăng lên đáng kể. Tuy nhiên, entropy thật sự của nó nhanh chóng rơi sau giá trị cực đại có thể có này tạo ra một “khe entropy”.

Trong quyển sách Tư duy Mới của Hoàng đế của ông, Roger Penrose đã phê bình quan điểm này với việc khẳng định rằng tình huống đảo ngược thời gian cũng nên áp dụng nếu và khi Vũ trụ cuối cùng co lại đến một Vụ Co Lớn. Khi nó co lại, khe entropy sẽ giảm cho đến khi một lần nữa nó đạt tới kích cỡ trong đó entropy là cực đại có thể có. Bất kì sự co lại nào thêm nữa cũng sẽ làm nén entropy xuống thêm, vi phạm định luật thứ hai.

Vậy làm thế nào chúng ta có thể hiểu sự bất đối xứng này giữa hai điểm kì dị? Lực hấp dẫn có thể mang lại nó hay không? Một sự khác biệt rõ ràng giữa pha giãn ra và pha co lại là ở pha giãn ra sẽ có một số điều kiện ban đầu nào đó làm cho Vũ trụ giãn ra lúc ban đầu. Mặt khác, pha co lại toàn bộ là do lực hút hấp dẫn của vật chất bên trong Vũ trụ. Như vậy, nguồn gốc vật lí của sự giãn nở và sự co lại là khác nhau. Nhưng người ta sẽ hài lòng nếu có thể giải thích sự phát triển của Vũ trụ theo khái niệm entropy.

Một khác biệt nữa ít được nói tới là một vũ trụ co lại rất lâu rồi sẽ không còn ngôi sao nào cháy sáng nữa. Nó sẽ gồm toàn là bức xạ nền lạnh lẽo, nhưng ngôi sao chết và những lỗ đen. Rõ ràng là một diện mạo entropy cao. Nhưng đây không phải là kịch bản khả dĩ duy nhất. Chúng ta hãy giả sử cho đơn giản rằng Vũ trụ đang co lại đó chỉ chứa ánh sáng (photon) năng lượng thấp và các lỗ đen. Hawking đã chứng minh rằng các lỗ đen bay hơi và do đó chúng ta có thể tưởng tượng một vũ trụ thật già – một vũ trụ có vừa đủ vật chất để nó cho kín, nghĩa là lực hấp dẫn phải mất một thời gian rất lâu mới làm ngừng và đảo ngược sự giãn nở - đến mức tất cả các lỗ đen có thể đã bay hơi hết. Chúng có để lại phía sau những điểm kì dị, trần, trống rỗng hay không thì chưa rõ, nhưng nếu chúng không để lại gì thì Vũ trụ cuối cùng chỉ gồm toàn là bức xạ lạnh lẽo.

___

³Kết luận ban đầu của Stephen Hawking và sự thừa nhận sai lầm của ông sau đó đã được người ta nói nhiều. Nhưng có những nhà vật lí khác, cũng lỗi lạc không kém, không hề đưa ra công khai sau khi lí thuyết của họ bị bác bỏ vì thiếu sự trung thực và lương thiện của Hawking. Chính Hawking từ nói rằng “nên có một tạp chí công khai trong đó các nhà khoa học có thể thừa nhận những sai lầm của mình. Nhưng có lẽ tạp chí đó sẽ chẳng có cộng tác viên nào.”