Trái tim của thuyết lượng tử – một số người sẽ nói là trái tim của ngành vật lí – chính là hàm sóng. Nhưng nó có thật sự là một loại sóng nào đó hay không? Một lí thuyết mới khiến số người ngờ vực ngày càng tăng thêm, như Jon Cartwright trình bày.
>> Xem Phần 1
Thực tại năng lượng
Năm 2010, các nhà vật lí toán Robert Spekkens thuộc trường Đại học Cambridge ở Anh (nay làm việc tại Viện Perimeter ở Waterloo, Canada) và Nicholas Harrigan thuộc trường Imperial College London (nay là giảng viên và sứ giả khoa học ở Manchester) đã đi tới một phương pháp mới xem xét vấn đề này. Một lần nữa hãy nghĩ tới hạt cổ điển đang chuyển động trong không gian một chiều, họ nói. Như trước đây, trạng thái tồn tại của nó có thể tại bất kì thời điểm nào hoàn toàn được đặc trưng bởi vị trí và xung lượng của nó. Nhưng bây giờ hãy nghĩ tới năng lượng của hạt, các nhà nghiên cứu đề xuất. Hạt có thể ở trong nhiều (có lẽ vô hạn) trạng thái tồn tại khác nhau, (x1,p1), (x2,p2), (x3,p3), vân vân, và vẫn có cùng năng lượng, E1. Hoặc nói ngược lại, một giá trị năng lượng, E1, sẽ không nhất thiết chỉ một trạng thái tồn tại. Điều này có nghĩa là chỉ riêng năng lượng – giống như hàm sóng nhận thức của Einstein, và hàm sóng “một phần thực tại” của Bohm – không đặc trưng đầy đủ cho thực tại.
Và chưa hết, bất chấp thiếu sót này, chúng ta biết vạn vật thật sự “có” năng lượng; nó chắc chắn là một bộ phận của thực tại, giống như hàm sóng của Bohm. Tại sao ư? Bí mật là như thế này, theo lời Spekkens và Harrigan: mặc dù một giá trị của năng lượng tương ứng với nhiều trạng thái tồn tại, nhưng điều cũng đúng là một trạng thái tồn tại – một cặp giá trị của vị trí và xung lượng – tương ứng với chỉ một giá trị của năng lượng. Nói cách khác, hai giá trị của năng lượng, E1 và E2, có thể tương ứng với một cặp giá trị vị trí và xung lượng, (x1,p1). (Ví dụ, hãy nghĩ tới năng lượng của một vật nặng gắn trên một lò xo, nếu khối lượng và độ cứng của lò xo là bằng nhau thì năng lượng đó có thể được viết là E = 1/2(p2+ x2).) Nếu hai giá trị của năng lượng thật sự tương ứng với một cặp giá trị vị trí và xung lượng, thì năng lượng sẽ không phải là một tính chất vật lí – nó sẽ không phải là một bộ phận của thực tại (Found. Phys. 40 125).
Định nghĩa của Spekkens và Harrigan là rõ ràng, và lần đầu tiên nêu ra một cách chính xác để phân biệt giữa quan điểm duy thực tồn tại và nhận thức. Nếu một trạng thái tồn tại λ1 chỉ ứng với một hàm sóng ψ1, thì các hàm sóng ít nhất phải là một bộ phận của thực tại – chúng phải tương ứng với một sóng vật lí – và quan điểm ontic (phe Bohm hoặc Everett) phải là đúng. Mặt khác, nếu một trạng thái tồn tại λ1có thể thỉnh thoảng tương ứng với hai hoặc nhiều hàm sóng, ψ1, ψ2, vân vân, thì các hàm sóng phải thể hiện sự hiểu biết chưa đầy đủ về thực tại, và quan điểm epistemic của Einstein phải là đúng.
Chứng minh cái chưa biết
Việc có tồn tại một sự phân biệt chính thức giữa quan điểm ontic và epistemic có nghĩa là phải có một cách xét xem quan điểm nào là đúng. Có lẽ một ai đó có thể chỉ ra rằng có những trường hợp khi một trạng thái ontic tương ứng với ít nhất hai hàm sóng khác nhau. Như thế sẽ chứng minh quan điểm Bohm và Everett là sai, và mọi người sẽ phải về phe Einstein – hoặc là từ bỏ quan điểm duy thực.
Hồi năm ngoái, các nhà vật lí Terry Rudolph và Matthew Pusey tại trường Imperial College London, cùng với nhà toán học Jonathan Barrett tại Royal Holloway, Đại học London, đã đón nhận thử thách đó. Họ đã phát triển một định lí xác định quan điểm duy thực nào, epistemic hay ontic, tương thích với các tiên đoán của cơ học lượng tử. Phần chứng minh của họ có phần phức tạp, nhưng có thể hiểu nó ở một cấp độ cơ bản với một thí nghiệm tưởng tượng, gồm một máy lăn-xúc xắc.
Máy lăn xúc xắc lăn một con xúc xắc bình thường, sáu mặt, theo một trong hai cách đặc biệt, tùy thuộc vào nút nào trong hai nút của nó bị nhấn. Nhấn nút kí hiệu “E” (chẵn) thì máy sẽ lăn theo một trong ba số chẵn của con xúc xắc: 2, 4 hoặc 6. Nhấn nút kí hiệu “P” (nguyên tố) thì sẽ máy sẽ lăn theo một trong ba số nguyên tố của con xúc xắc: 2, 3 hoặc 5.
Bước tiếp theo trong thí nghiệm tưởng tượng trên là lấy hai máy lăn xúc xắc này và bố trí chúng sao cho hai con xúc xắc lăn đồng thời vào một cái hộp đo. Bốn bóng đèn trên hộp đo biểu thị một trong bốn kết hợp khả dĩ chẵn và nguyên tố: "not EE", "not EP", "not PE" và "not PP" (hình 3a). Các đèn lúc đầu cháy màu đỏ, nhưng một khi hai con xúc xắc đi vào trong hộp và được đo, thì bất kì đèn nào tương ứng với kết cục thực tế sẽ chuyển sang xanh lục.
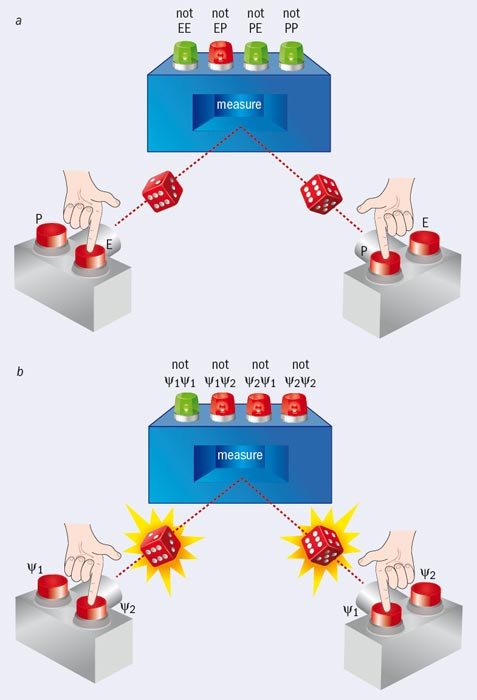
Hình 3.Trong thí nghiệm tưởng tượng của Pusey, Barrett và Rudolph, hai chiếc máy mỗi máy lăn một con xúc xắc ở một trong hai trạng thái vào một hộp đo. Ở hình (a), hai con xúc xắc lăn vào trạng thái cổ điển chẵn (E) hoặc nguyên tố (P). Ở hình (b), hai con xúc xắc lăn vào những trạng thái lượng tử, ψ1 hoặc ψ2. Câu hỏi đặt ra là liệu cái hộp luôn luôn có thể bật một trong những kết cục màu xanh hay không? Nếu không, thì hai trạng thái xúc xắc ban đầu phải là epistemic. Nhưng nếu cái hộp luôn luôn có thể bật một đèn xanh, thì các trạng thái đó phải là ontic – chúng phải tương ứng với ít nhất là một bộ phận của thực tại.
Rudolph, Pusey và Barrett đã nêu một câu hỏi trông như đơn giản: cái hộp đo sẽ luôn luôn có thể bật ít nhất một đèn xanh hay không? Thoạt trông thì có vẻ câu trả lời là có. Nếu máy lăn một mặt 6 và một mặt 5, chẳng hạn, thì cái hộp sẽ tính được là mặt 6 chỉ có thể được lập bởi nút chẵn “E”, còn mặt 5 chỉ có thể được lập bởi nút nguyên tố “P”; tổ hợp nút nhấn phải là EP. Do đó, “not EP” sẽ vẫn đèn đỏ, còn tất cả những đèn kia sẽ chuyển sang xanh – tức là các đèn "not EE", "not PE" và "not PP". Nếu máy lăn một mặt 2 và một mặt 5, thì tình huống phức tạp hơn bởi vì mặt 2 có thể được lập bởi hoặc nút “chẵn” hoặc nút “nguyên tố”; hoặc tổ hợp nút EP hoặc PP có thể dẫn tới kết cục này. Tuy nhiên, cái hộp sẽ vẫn có thể bật hai đèn xanh – các đèn phía trên "not EE" vaf "not PE". Khi ấy, thoạt trông thì, vâng, cái hộp luôn luôn có thể bật một đèn xanh.
Nhưng nếu máy lăn một cặp hai mặt 2 thì sao? Bây giờ thì cái hộp đo gặp rắc rối. Hai mặt 2 có thể được lập bởi hoặc nút “chẵn” hoặc nút “nguyên tố”, và không kết quả nào có thể bị loại trừ - nghĩa là, không có đèn nào có thể bật sang xanh. Thật vậy, tình huống đặc biệt này chứng minh rằng các nút “chẵn” và nút “nguyên tố” đang lập các trạng thái epistemic, bởi vì – theo định nghĩa của Spekkens và Harrigan – chúng có thể thỉnh thoảng tương ứng với cùng một trạng thái ontic: mặt 2.
Bây giờ hãy thay con xúc xắc bằng phiên bản lượng tử, theo Rudolph và các đồng sự. Thay vì lăn vào trạng thái hoặc chẵn hoặc nguyên tố, chiếc máy “lăn” con xúc xắc lượng tử mới vào một trong hai hàm sóng, ψ1 và ψ2. Đồng thời, kết cục của hộp đo bây giờ là "not ψ1ψ1", "not ψ1ψ2", "not ψ2ψ1" và "not ψ2ψ2" (hình 3b). Tuy nhiên, câu hỏi vẫn còn đó: liệu cái hộp sẽ luôn luôn có thể bật ít nhất một đèn xanh hay không? Nếu có một trường hợp nó không thể, và cả bốn đèn vẫn cháy đỏ, thì nó sẽ chứng minh rằng ít nhất một trong hai chiếc máy đã lăn một con xúc xắc vào một trạng thái ontic hoặc “con số” có thể tương ứng với hoặc ψ1 hoặc ψ2 – như trong phiên bản cổ điển, trong đó trạng thái ontic của “mặt 2” có thể ứng với hoặc chẵn hoặc nguyên tố. Với một trường hợp như vậy, các nhà vật lí sẽ không biết con số ontic bí ẩn đó là gì, nhưng họ sẽ biết nó có tồn tại – và như thế là đủ để chứng minh rằng hàm sóng là epistemic.
Nhưng đây là cái bất ngờ: cơ học lượng tử dự đoán điều này là không thể. Nó tiên đoán rằng cái hộp sẽ luôn luôn bật một đèn xanh, cho dù cặp hàm sóng ψ1 và ψ2 được chọn (Nat. Phys. 8 475).
Jon Cartwright (Physics World, tháng 5/2013)