Trái tim của thuyết lượng tử – một số người sẽ nói là trái tim của ngành vật lí – chính là hàm sóng. Nhưng nó có thật sự là một loại sóng nào đó hay không? Một lí thuyết mới khiến số người ngờ vực ngày càng tăng thêm, như Jon Cartwright trình bày.
>> Xem Phần 2
Xin chào thực tại
Định lí của Pusey, Barrett và Rudolph, bây giờ gọi là định lí PBR, về cơ bản là đưa ra một tối hậu thư. Nếu cơ học lượng tử là đúng, thì hàm sóng không thể là epistemic – nó không thể đơn thuần biểu diễn một sự hiểu biết cục bộ của nhà thực nghiệm về thực tại. Thay vậy, nó phải là ontic và tương ứng trực tiếp với hoặc một phần của thực tại (như Bohm nói) hoặc toàn bộ thực tại (như Everett nói).
Tất nhiên, cơ học lượng tử có thể sai – và thật vậy, các nhà nghiên cứu nêu ra một dấu hiệu thực nghiệm để kiểm tra các tiên đoán cơ lượng tử do định lí của họ đưa ra. Tuy nhiên, bạn phải là một người có tư duy thoáng để cược vào kết cục epistemic – và sẽ có một cơ hội khi không có đèn nào bật sang xanh. Trong suốt lịch sử của nó, chưa có dự đoán nào của cơ học lượng tử từng bị sai. Thực tế rất rõ ràng là tiên đoán epistemic trái với cơ học lượng tử hàm ý rằng hàm sóng tương ứng với ít nhất là một phần của thực tại, với một loại sóng vật lí nào đó. Einstein nổi tiếng với việc khăng khăng rằng Chúa “không chơi xúc xắc”; tuy nhiên, hai con xúc xắc đã lăn phản lại ông.
Nhìn chung, những người theo phe Einstein có ba lựa chọn (xem lại hình 2). Nếu họ muốn giữ hàm sóng là epistemic, thì họ có thể từ bỏ thuyết duy thực khoa học, mặc dù nhiều người sẽ xem đó là một hi sinh lớn. Nhưng việc giữ quan điểm duy thực còn lại hai lựa chọn. Một lựa chọn là hàm sóng là một bộ phận cảu thực tại – như trong cơ học Bohm, trong đó sóng dẫn hướng cho chuyển động của hạt. Lựa chọn kia là hàm sóng là toàn bộ thực tại – như trong cách hiểu “đa thế giới” của Everett về cơ học lượng tử.
David Wallace, một nhà triết học vật lí tại trường Đại học Oxford ở Anh, là một người đề xướng cách hiểu đa thế giới. Ông tin rằng định lí PBR mô tả kết quả quan trọng nhất trong những nền tảng lượng tử trong sự nghiệp của ông. (Năm nay ông 36 tuổi.) “Đó là tin tốt lành khi nhìn từ quan điểm của những ai muốn cách hiểu của Everett là đúng,” ông nói. “Mặc dù có tính cảnh giác cao, nhưng tôi không nhất thiết muốn cách hiểu của Everett là đúng; tôi muốn biết cái gì đang diễn ra thôi.” Wallace trình bày rằng đã có những lí do hay ho để mà hoài nghi quan điểm epistemic. Một lí do như thế, ông nói, là bằng chứng thực nghiệm rằng các hạt giao thoa với nhau – một tính chất thật sự giống sóng, cho thấy hàm sóng không đơn thuần là sự hiểu biết bộ phận về thực tại.
Tuy nhiên, quan điểm Einstein chưa thua cuộc. Định lí PBR xây dựng trên những giả thuyết nhất định, một giả thuyết chính là những hệ được xử lí độc lập đó có những trạng thái vật lí độc lập nhau. Các nhà lí thuyết lượng tử và các nhà triết học bây giờ có thể loại ra những giả thuyết này – mặc dù nó sẽ không dễ dàng gì. “Tôi sẽ bất ngờ nếu ai đó không nghĩ ra được một lí thuyết nào đó né tránh [các giả thuyết PBR],” Wallace nói. “Hiện nay, lí thuyết đó trông giả tạo sao ấy, tôi không biết nữa. Cái tôi nhìn thấy cho đến nay... khiến tôi có chút tuyệt vọng.”
Tuy nhiên, cơ học lượng tử đã buộc các nhà vật lí từ bỏ nhiều giả thuyết ràng buộc sít sao của chúng về tự nhiên. Một trong những lí do khiến Einstein đi tới quan điểm epistemic là vì đề xuất rằng cơ học lượng tử có thể áp dụng các biến đổi tức thời trong những hệ ở rất xa nhau, một hiện tượng ông gọi là “tác dụng ma quỷ từ xa”. Sự phản đối của ông mất tác dụng khi nhà vật lí người Bắc Ireland, John Bell, công bố một định lí vào năm 1964, chứng minh rằng mọi lí thuyết của tự nhiên – cho dù là epistemic hay không – thật ra phải là phi định xứ.
Rudolph – bản thân ông là người ủng hộ cách hiểu epistemic, bất chấp thực tế là minh chứng của ông lại ủng hộ cho cách hiểu ontic – tin rằng có một cơ sở vật lí nằm ngoài hàm sóng, nhưng ông chỉ có thể suy biện mà thôi. “Mặc dù nó trông rất trừu tượng, nhưng cái chúng tôi đang nói tới theo một nghĩa nào đó là bó buộc với không gian và thời gian,” ông nói.
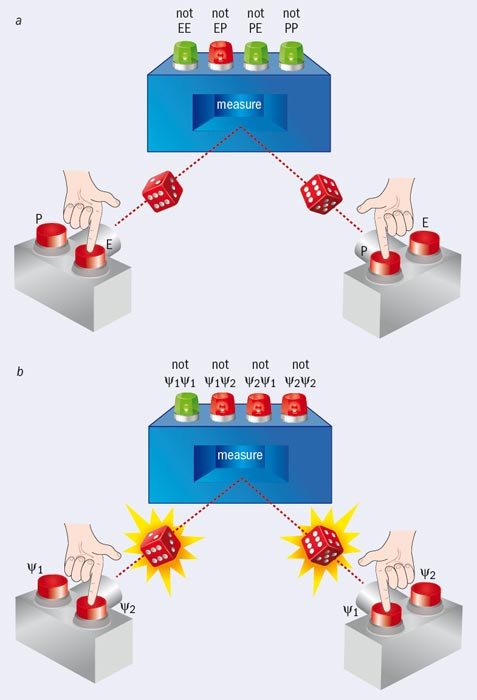
Hình 4. Tìm hiểu thí nghiệm
Thí nghiệm xúc xắc theo cơ học lượng tử
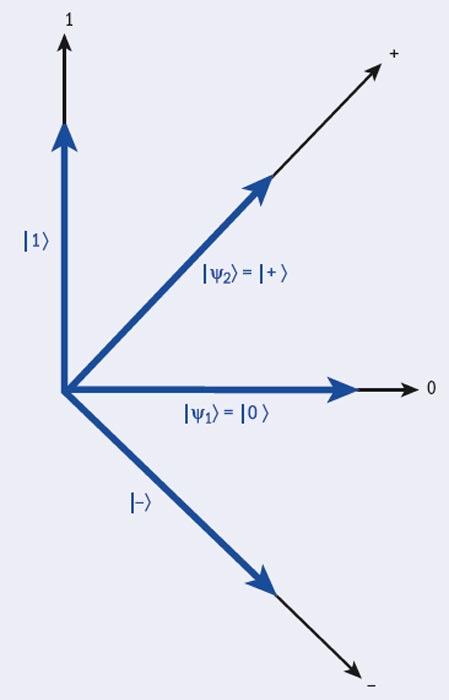
Để thấy cơ học lượng tử xử lí như thế nào với thí nghiệm tưởng tượng con xúc xắc ở hình 3, ta phải chuyển sang dạng thức vector. Hãy biểu diễn hàm sóng thứ nhất |ψ1〉là |0〉và hàm sóng thứ hai |ψ2〉là 1/√2(|0〉 +|1〉) = |+〉. Nói đơn giản. điều này có nghĩa là |ψ1〉đi cùng với một vector đơn vị trong chiều “0”, còn |ψ2〉đi cùng với một vector đơn vị hướng lưng chừng giữa chiều “0” và “1”, để cho tiện ta viết là chiều “+”. (Bội số 1/√2 là để giữ cho các vector dài một đơn vị.) Các vector |0〉và |1〉vuông góc hay “trực giao” với nhau, nghĩa là cái gọi là tích nội của chúng, 0|1〉, bằng không. Vector trực giao với |+〉là |–〉 = 1/√2(|0〉 – |1〉).
Khi con xúc xắc lượng tử lăn vào hộp đo, thì xác suất mỗi đèn bật sang xanh, theo cơ học lượng tử, được tính theo những cơ sở sau đây:
|not ψ1ψ1〉= 1/√2(|0〉⊗ |1〉+ |1〉⊗ |0〉)
|not ψ1ψ2〉 = 1/√2(|0〉⊗ |–〉+ |1〉⊗ |+〉)
|not ψ2ψ1〉= 1/√2(|+〉⊗ |1〉+ |–〉⊗ |0〉)
|not ψ2ψ2〉= 1/√2(|+〉⊗ |–〉+|–〉⊗ |+〉)
Chúng ta hãy giả sử máy lăn xúc xắc đưa một con xúc xắc vào hàm sóng ψ1 (|0〉) và con xúc xắc kia vào hàm sóng ψ2 (|+〉). Căn bậc hai của xác suất, P, phải được tính trước, và để có kết cục, nói ví dụ, "not ψ1ψ1", giá trị này được cho bởi phép tính:
√P = 〈0|〈+||not ψ1ψ1〉
= 1/√2(〈0|0〉⊗ 〈+|1〉+〈0|1〉 ⊗〈+|0〉)
= 1/√2(1/√2)
= 1/2
Xác suất của đèn bật xanh "not ψ1ψ1" do đó là (1/2)2 = ¼. Những tính toán tương tự cho thấy xác suất của đèn xanh phía trên “not ψ2ψ2” cũng là 1/4, còn xác suất của đèn xanh phía trên "not ψ2ψ1" là 1/2. Xác suất của kết cục "not ψ1ψ2" – như người ta trông đợi, biết rằng hai con xúc xắc trong trạng thái ψ1 và ψ2 – là bằng không; đèn của nó chắc chắn sẽ vẫn cháy đỏ.
Điều này có nghĩa là hộp đo sẽ bật một trong ba đèn sang xanh: "not ψ1ψ1", "not ψ2ψ2" hoặc "not ψ2ψ1". Thật vậy, hóa ra bất kì kết hợp nào của các hàm sóng chuẩn bị trên hai con xúc xắc – ψ1 và ψ1; ψ2 và ψ1, vân vân – phải biểu thị một đèn xanh. Hoặc nói cách khác, theo cơ học lượng tử, không có khả năng xác suất của bốn kết cục “not” đều bằng không (đó là cái xảy ra trong trường hợp con xúc xắc cổ điển với một cặp mặt 2).
Mặc dù lập luận trên sử dụng hai hàm sóng đặc biệt làm ví dụ, nhưng Rudolph, Barrett và Pusey đã thiết lập được một lập luận khái quát cho mọi cặp hàm sóng bất kì.
- Jon Cartwright (Physics World, tháng 5/2013)
![Sách[SMB]: Sổ Tay Kiến Thức Trung Hoc Cơ Sở: Vật Lí + Hóa Học](https://thuvienvatly.com/images/deals/thumb/sach-smb-so-tay-kien-thuc-trung-hoc-co-so-vat-li-hoa-hoc.jpg)
