- Ian Stewar , Đại học Warwick, Anh quốc
Chết hay sống
Vào năm 1927, Erwin Schrödinger đã viết ra một phương trình cho những sóng lượng tử. Nó phù hợp với những thí nghiệm một cách tuyệt vời đồng thời vẽ nên một bức tranh của một thế giới rất khác lạ, trong đó những hạt sơ cấp như electron không phải là vật thể rõ ràng, mà là những đám mây xác suất. Spin của electron giống như một đồng tiền có thể nửa sấp nửa ngữa cho đến khi nó rơi xuống bàn. Không lâu sau đó, các nhà lí thuyết lại lo lắng không yên trước mọi tính chất lạ lượng tử, ví dụ những con mèo vừa sống vừa chết, và những vũ trụ song song trong đó Adolf Hitler là kẻ chiến thắng cuộc chiến tranh thế giới lần thứ hai.
Cơ học lượng tử không bị ràng buộc với những bí ẩn triết lí như vậy. Hầu như mọi vật dụng hiện đại – máy vi tính, điện thoại di động, máy chơi game, xe hơi, tủ lạnh, lò vi sóng – đều chứa những con chip nhớ gốc transistor, dụng cụ có sự hoạt động dựa trên cơ học lượng tử của chất bán dẫn. Những công dụng mới cho cơ học lượng tử xuất hiện gần như hàng tuần. Các chấm lượng tử - những miếng nhỏ xíu của một chất bán dẫn – có thể phát ra ánh sáng thuộc mọi màu sắc và được sử dụng để ghi ảnh sinh học, trong đó chúng thay thế cho những chất nhuộm truyền thống, thường là độc hại. Các kĩ sư và nhà vật lí đang cố gắng phát minh ra máy vi tính lượng tử, một dụng cụ có thể thực hiện song song nhiều phép tính khác nhau, giống hệt như con mèo vừa sống vừa chết.
Laser là một ứng dụng nữa của cơ học lượng tử. Chúng ta sử dụng chúng để đọc thông tin từ những lỗ nhỏ li ti trên đĩa CD, DVD và đĩa Blu-ray. Các nhà thiên văn sử dụng laser để đo khoảng cách từ Trái đất đến mặt trăng. Thậm chí có thể phóng những tên lửa vũ trụ lên từ Trái đất với sức đẩy là một chùm laser mạnh.
Chương cuối trong câu chuyện này có xuất xứ từ một phương trình giúp chúng ta hiểu ý nghĩa của sóng. Nó bắt đầu vào năm 1807, khi Joseph Fourier nghĩ ra một phương trình cho dòng nhiệt. Ông đã gửi một bài báo về nói về nó đến Viện hàn lâm Khoa học Pháp nhưng bị từ chối. Vào năm 1812, viện hàn lâm Pháp đưa vấn đề nhiệt thành đề tài của giải thưởng hàng năm của viện. Fourier lại gửi một bài báo dài hơn, có hiệu chỉnh – và đã giật giải.
Cái hấp dẫn nhất của bài báo giành giải thưởng của Fourier không phải là phương trình, mà là cách ông giải nó. Một bài toán điển hình là tìm xem nhiệt độ dọc theo một thanh mỏng thay đổi như thế nào theo thời gian, cho biết trước đặc điểm nhiệt độ ban đầu. Fourier có thể giải phương trình này một cách nhẹ nhàng nếu như nhiệt độ biến thiên như một sóng hình sin dọc theo chiều dài thanh. Vì thế, ông biểu diễn một đặc trưng phức tạp hơn là sự kết hợp của những đường hình sin với bước sóng khác nhau, giải phương trình cho mỗi đường cong hình sin thành phần, và cộng tất cả những nghiệm này lại với nhau. Fourier khẳng định phương pháp này đúng cho mọi đặc trưng nhiệt độ bất kì, thậm chí đúng cả với trường hợp trong đó nhiệt độ có giá trị nhảy cóc. Tất cả những gì phải làm là cộng gộp một số vô hạn những đóng góp từ những đường cong hình sin với tần số lớn dần.
Dẫu vậy, bài báo mới của Fourier đã bị chỉ trích là không đủ chặt chẽ, và một lần nữa viện hàn lâm Pháp từ chối đăng tải. Vào năm 1822, Fourier phớt lờ mọi phản đối và cho công bố lí thuyết của ông dưới dạng một quyển sách. Hai năm sau đó, ông tự bổ nhiệm mình làm thư kí của viện hàn lâm, dí mũi của ông vào những kẻ chỉ trích ông, và cho đăng bài báo gốc của ông trong tập san của viện. Tuy nhiên, những người chỉ trích chưa chịu dừng lại. Các nhà toán học bắt đầu nhận ra rằng những chuỗi vô hạn là những thứ nguy hiểm; chúng không luôn luôn hành xử giống như những tổng hữu hạn, đẹp đẽ. Việc giải quyết những vấn đề này hóa ra là hết sức khó khăn, nhưng phán quyết cuối cùng là quan điểm của Fourier có thể được làm cho chặt chẽ bằng cách ngoại suy ra những đặc trưng rất không đều. Kết quả là phép biến đổi Fourier, một phương trình xem một tín hiệu biến thiên theo thời gian là tổng của một chuỗi những đường cong hình sin thành phần và tính ra biên độ và tần số của chúng.

Trường phái Pythagoras đã tính được những cái gì làm cho sợi dây phát ra âm thanh du dương.
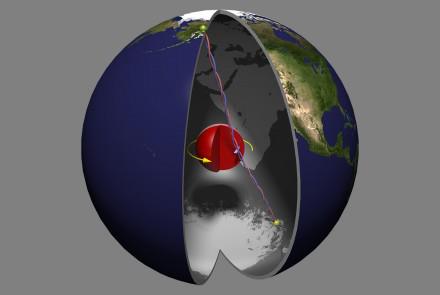
Ngày nay, phép biến đổi Fourier ảnh hưởng đến cuộc sống của chúng ta theo vô số kiểu. Chẳng hạn, chúng ta có thể sử dụng nó để phân tích tín hiệu dao động tạo ra bởi một trận động đất và để tính ra những tần số mà năng lượng truyền bởi mặt đất chấn động là lớn nhất. Một bước tiến tới xây dựng những công trình chịu được động đất là đảm bảo rằng tần số riêng của công trình khác với tần số của động đất.
Những ứng dụng khác bao gồm việc loại tạp âm ra khỏi những bản ghi âm cũ, tìm kiếm cấu trúc của ADN bằng ảnh chụp tia X, cải thiện sự thu nhận vô tuyến và ngăn cản những dao động không mong muốn ở xe hơi. Thêm một ứng dụng nữa mà đa số mọi người chúng ta sử dụng thường xuyên mà không để ý, đó là chụp ảnh kĩ thuật số.
Nếu bạn tính xem cần bao nhiêu thông tin để biểu diễn màu sắc và độ sáng của mỗi pixel trong một bức ảnh kĩ thuật số, bạn sẽ phát hiện ra rằng một chiếc camera kĩ thuật số nhồi nhét vào thẻ nhớ của nó lượng dữ liệu nhiều gấp mười lần cái thẻ nhớ có thể chứa. Camera làm công việc này bằng cách sử dụng sự nén dữ liệu JPEG gồm năm bước nén khác nhau. Một trong số chúng là một phiên bản kĩ thuật số của phép biến đổi Fourier, nó hoạt động với một tín hiệu không thay đổi theo thời gian mà thay đổi từ đầu này qua đầu kia bức ảnh. Cơ sở toán học hầu như là giống hệt. Bốn bước còn lại tiếp tục làm giảm dữ liệu thêm nữa, đến khoảng bằng một phần mười lượng ban đầu.
Đây mới chỉ là bảy trong nhiều phương trình mà chúng ta bắt gặp hàng ngày, nhưng không nhận ra chúng đang hiện diện ở đấy. Nhưng sự tác động của những phương trình này đối với lịch sử thì sâu sắc hơn nhiều. Một phương trình thật sự mang tính cách mạng có thể có sự tác động đối với sự tồn tại của loài người lớn hơn cả mọi nhà vua và hoàng hậu có mưu đồ choán đầy những quyển sử học của chúng ta.
Có (hoặc có thể có) một phương trình, trên hết thảy, mà các nhà vật lí và nhà vũ trụ học đặt hết niềm tin yêu vào đấy: một lí thuyết của tất cả thống nhất cơ học lượng tử và thuyết tương đối. Nổi tiếng nhất trong số nhiều ứng cử viên là lí thuyết siêu dây. Nhưng như mọi người chúng ta đều biết, các phương trình của chúng ta cho thế giới vật chất có lẽ chỉ là những phiên bản đơn giản hóa không bắt giữ được cấu trúc sâu sắc của thực tại. Ngay cả nếu tự nhiên có tuân theo những định luật vạn vật, thì chúng có thể không được biểu diễn dưới dạng những phương trình.
Một số nhà khoa học nghĩ rằng đã đến lúc chúng ta từ bỏ những phương trình truyền thống để theo đuổi những thuật toán – những công thức khái quát hơn để tính toán mọi thứ, kể cả việc ra quyết định. Nhưng cho đến những ngày ấy, nếu có, sự hiểu biết sâu sắc nhất của chúng ta về các định luật của tự nhiên sẽ tiếp tục có dạng thức những phương trình, và chúng ta sẽ học cách tìm hiểu chúng và thích ứng với chúng. Các phương trình có thành tựu của chúng, Chúng thật sự đã làm biến chuyển thế giới và chúng sẽ lại tiếp tục làm thế giới biến chuyển.
Nguồn gốc của các phương trình
Người Babylon và Hi Lạp cổ đại đã biết về những phương trình, mặc dù họ viết chúng bằng lời và bằng hình ảnh. Trong 500 năm qua, các nhà toán học và nhà khoa học đã sử dụng những kí hiệu, và một kí hiệu quan trọng chính là cái dấu bằng nhau. Lạ thay, chúng ta biết ai phát minh ra nó, và tại sao nữa. Chính là Robert Recorde, người vào năm 1557 đã viết ra chuyên luận The Whetstone of Witte: "Để tránh lặp lại một cách nhạt nhẽo những từ này: bằng với, tôi sẽ viết nó dưới dạng một kiểu tôi thường làm: một cặp song song…”
Định lí và lí thuyết
Một số phương trình biểu diễn mối liên hệ lôgic giữa những đại lượng toán học, và nhiệm vụ của nhà toán học là chứng minh chúng là đúng. Những phương trình khác cung cấp thông tin về một đại lượng chưa biết; nhiệm vụ ở đây là giải phương trình và tìm biến chưa biết đó. Các phương trình toán học thuần túy thường thuộc loại thứ nhất: chúng cho biết những khuôn mẫu và những quy tắc trong toán học. Định lí Pythagoras, một phương trình biểu diễn theo ngôn ngữ hình học, là một ví dụ. Với những giả thiết hình học cơ bản của Euclid thì định lí Pythagoras là đúng.
Các phương trình trong toán học ứng dụng và vật lí toán thường thuộc loại thứ hai. Chúng biểu diễn những tính chất của vũ trụ mà, trên nguyên tắc, có thể không như thế. Ví dụ, định luật hấp dẫn Newton cho chúng ta biết cách tính lực hút giữa hai vật thể. Giải phương trình thu được cho chúng ta biết các hành tinh quay xung quanh mặt trời như thế nào hoặc làm thế nào vẽ quỹ đạo cho một tàu thám hiểm vũ trụ. Nhưng định luật Newton không phải là một định lí toán học; định luật hấp dẫn có thể khác đi. Thật vậy, nó đã khác đi: thuyết tương đối tổng quát của Einstein đã nâng cấp lí thuyết của Newton. Và dẫu thế, lí thuyết đó cũng không thể là ngôn từ cuối cùng.
Dịch bởi Trần Nghiêm – thuvienvatly.com
Theo New Scientist









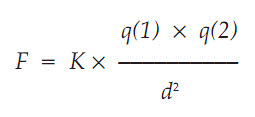








![[Ảnh] Bay tự do trong không gian](/bai-viet/images/2012/01/freeflyer_nasa_900.jpg)