Lỗ đen, lỗ sâu đục và cỗ máy thời gian (Phần 73)

Chương 10

CHÚNG TA BIẾT ĐƯỢC NHỮNG GÌ?

“Bây giờ tôi tin rằng nếu tôi hỏi một câu hỏi thậm chí đơn giản hơn – ví dụ, Anh muốn nói gì với khối lượng? hay sự gia tốc, đó là tương đương khoa học của câu nói, Anh biết đọc không? – chẳng có hơn một trong số mười người có học thức sẽ cảm thấy tôi đang nói cùng thứ ngôn ngữ với họ. Vì thế, dinh thự của nền vật lí hiện đại càng đồ sộ thì phần đông những người thông minh nhất ở thế giới phương tây sẽ có kiến thức về nó ngang ngửa như tổ tiên tiền sử của họ mà thôi.”

C P Snow, Hai nền văn hóa

“Các nhà thơ nói rằng khoa học đã cướp mất cái đẹp của những vì sao – chúng chỉ là những đám nguyên tử chất khí mà thôi. Chẳng có gì “chỉ là” hết. Tôi cũng nhìn thấy những vì sao trên bầu trời đêm sa mạc, và tôi cảm nhận chúng. Nhưng tôi nhìn thấy nhiều hơn hay ít hơn chứ? Sự mênh mông của bầu trời làm mở rộng trí tượng tượng của tôi – đôi mắt nhỏ bé của tôi có thể bắt gặp ánh sáng một triệu năm tuổi; một khung trời bao la mà tôi là một bộ phận trong đó… Đâu là khung trời, hay ý nghĩa, hay nguyên nhân? Tôi không làm tổn hại đến bí ẩn biết ít nhiều về nó. Đó là sự thật kì diệu hơn nhiều so với bất kì người nghệ sĩ nào thời quá khứ từng tưởng tượng ra. Vậy tại sao các nhà thơ thời nay không nói về nó nữa?”

Richard Feynman, Những bài giảng vật lí của Feynman, Tập 1

Ở chương cuối này, tôi muốn dành để nói đôi điều về cái chúng ta tin rằng chúng ta biết về Vũ trụ của chúng ta và xét xem chúng ta có thể phát triển tiến bộ như thế nào.

Mẹ của mọi lí thuyết

Lí thuyết hình học của sự hấp dẫn (thuyết tương đối tổng quát) của Einstein và cơ học lượng tử là hai thành tựu vĩ đại của nền vật lí học thế kỉ thứ hai mươi, là cột trụ cho mọi thứ khác mà chúng ta đã biết về thế giới vật chất của chúng ta và ngoài đó nữa, cả trước đó và kể từ đó. Chúng đều mô tả rất thành công những phương diện cơ bản nhất của thực tại. Nhưng như tôi đã nói ở chương trước, vấn đề là chúng không tương thích với nhau. Chúng xây dựng trên những loại toán học rất khác nhau và có những quy tắc và những nguyên lí cơ bản hoàn toàn tách biệt. Thuyết tương đối tổng quát sụp đổ tại các kì dị và các vòng lặp thời gian kín, còn cơ học lượng tử không mô tả được lực hấp dẫn trong khuôn khổ của nó. Vậy chúng ta tiến được bao xa đến một lí thuyết của sự hấp dẫn lượng tử; một ‘lí thuyết của tất cả’ sẽ chứa bên trong cấu trúc toán học của nó những nguyên tắc và nguyên lí của cả thuyết tương đối và cơ học lượng tử? Vâng, như chúng ta đã thấy trong thế kỉ hai mươi và bước sang thế kỉ hai mươi mốt, có lẽ chúng ta đã có một lí thuyết như thế trong tầm tay rồi.

Einstein đã hoàn thành lí thuyết tương đối tổng quát của ông vào năm 1915, và rồi giữ một vai trò tương đối thứ yếu (không có ý định chơi chữ nhé) trong sự phát triển sau đó của thuyết lượng tử chiếm lĩnh phần lớn những nhà khoa học hàng đầu khác trên thế giới trong hơn mười năm tiếp sau đó. Nhưng một khi các khái niệm và cơ sở toán học đã được sắp xếp thì chúng ta cần làm những gì nữa? Một số nhân vật lớn thời đại Einstein sẽ không chịu dừng lại với việc chấm lên những chữ ‘i’ và gạch ngang những chữ ‘t’. Vì thế, trong ba mươi năm cuối đời, ông đã đi tìm, nhưng không thành công, cái gọi là một lí thuyết trường thống nhất; một lí thuyết sẽ kết hợp thuyết tương đối tổng quát không phải với cơ học lượng tử mà với thuyết ánh sáng (hay chính xác hơn là thuyết điện từ). Einstein đã thử một số cách tiếp cận nhưng chưa lần nào dấn sâu nỗi. Được biết, người ta đã tìm thấy những bài báo với lí thuyết chưa hoàn thành của ông trên bàn làm việc của ông sau khi ông qua đời.

Cơ sở toán học sáng giá nhất, nhưng cũng khó hiểu nhất, cho một lí thuyết thống nhất mà Einstein tìm kiếm là từ hai nhà toán học: Theodor Kaluza người Ba Lan, và Oska Klein người Thụy Điển. Kaluza đã tiến hành mọi công việc cơ bản và, vào năm 1919, đã gửi một bài báo cho Einstein trong đó ông đề xuất một cách giải thích bức xạ điện từ trong khuôn khổ của thuyết tương đối tổng quát.

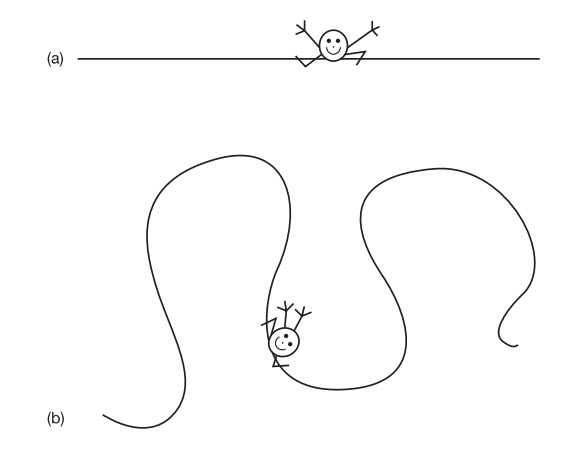
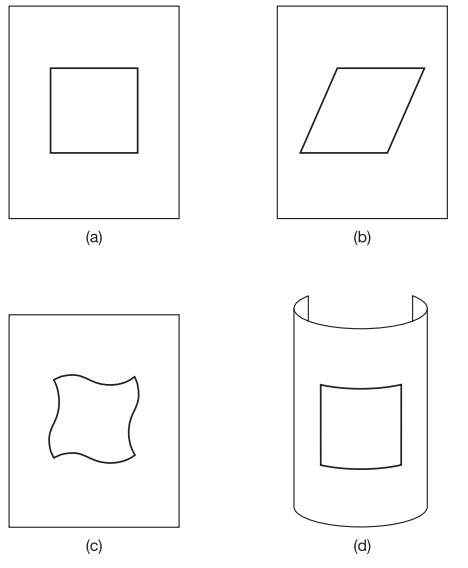
Kaluza chứng minh rằng cái cần thiết để thu được lời giải thích này là viết các phương trình của ông không phải trong không thời gian 4D mà là 5D, bằng cách gộp thêm một chiều không gian bổ sung nữa. Mặc dù điều này nghe thật tùy tiện và xa rời với cái chúng ta xem là thực tế, nhưng nó tương đối dễ tiến hành về mặt toán học, nơi chúng ta có thể cộng bao nhiêu chiều mà chúng ta muốn. Nhưng chiều không gian thứ tư mà Kaluza đề xuất này là có thực hay không? Chắc chắn chúng ta không nhận thức được nó nếu nó hiện diện. Nhưng khi ông gộp thêm chiều không gian bổ sung này, Kaluza tìm thấy rằng ánh sáng, thay vì là một trường điện từ đang dao động trong không gian 3D, thật ra là một dao động của chiều thứ năm này. Cho nên bạn cứ yên tâm tiến lên thôi. Nhưng đừng lo, tôi cũng chẳng thật sự hiểu điều này có nghĩa là gì. Tất cả những gì chúng ta có thể nói là nó cố gắng giải thích nguồn gốc của ánh sáng ở một cấp độ hình học, cơ bản hơn giống như kiểu Einstein đã mô tả sự hấp dẫn là sự cong của không thời gian 4D. Không những thế, chiều thứ năm này không trải ra theo đường thẳng như ba chiều không gian kia mà tự ‘cuộn lại’. Một cách đơn giản hình dung điều này có ý nghĩa gì là hãy nghĩ tới thế giới 2D. Hãy tưởng tượng không gian 2D phẳng cuộn lại thành một hình trụ. Một trong hai chiều của nó – chiều hướng theo trục dài của nó – vẫn không biến đổi, còn chiều kia khép kín thành một vòng tròn.

Tất nhiên, vấn đề là, bất chấp nét đẹp toán học của lí thuyết Kaluza, chẳng có mảnh bằng chứng thực nghiệm nào cho thấy chiều thứ năm này thật sự tồn tại. Ngay cả Einstein, trong khi ấn tượng trước cách Kaluza thống nhất ánh sáng và sự hấp dẫn, cũng không sẵn lòng tin vào thực tế có một chiều thứ năm. Nói chung, ông có chút miễn cưỡng khi đưa vào xét khái niệm không thời gian bốn chiều làm điểm xuất phát. Ít nhất thì bốn chiều đó (một chiều thời gian và ba chiều không gian) là có thật. Nguyên nhân chính cho sự hoài nghi của Einstein và những người khác là vì chúng ta chưa bao giờ nhìn thấy chiều bổ sung này. Câu hỏi này được trả lời vào năm 1926 khi Oskar Klein đề xuất rằng lí do người ta không phát hiện ra chiều thứ năm là vì nó cuộn lại thành một vòng tròn nhỏ đến mức nó nhỏ hơn hàng tỉ lần so với một nguyên tử. Một lần nữa, hãy nghĩ tới một trong hai chiều của thế giới 2D cuộn vòng lại thành bề mặt của một hình trụ. Klein nói rằng hình trụ đó sẽ mỏng đến mức trông nó như một đường thẳng. Nghĩa là thế giới 2D đó sẽ trông có một chiều và chúng ta sẽ nói rằng chiều thứ hai bị che giấu. Tôi e rằng tôi không thể nêu ra cho bạn một ví dụ cao chiều hơn ví dụ này bởi vì, như chúng ta đã thấy ở Chương 1, chúng ta cần một chiều thứ ba để uốn cong một trong hai chiều của thế giới 2D đó vào. Và bạn nghĩ bạn đã vứt bỏ được món nợ nhức đầu về các chiều lại phía sau lưng.

Nhưng bạn chưa phủi tay được đâu! Hãy tiếp tục nào.