Cỗ máy thời gian dây vũ trụ
Một cách khả dĩ nữa hiện thực hóa cỗ máy thời gian Tipler là sử dụng dây vũ trụ. Chúng ta đã thấy trong chương trước dây vũ trụ có thể hữu ích như thế nào trong việc giữ cho cổ họng của lỗ sâu đục mở ra. Nhưng một lần nữa, đây có lẽ là loại chất liệu vừa vặn mà chúng ta đang tìm kiếm. Nó sẽ dài vô hạn và nhất định sẽ đủ đậm đặc. Toàn bộ những gì chúng ta cần làm là để cho nó quay đủ nhanh. Tất nhiên ở đây thật sự có giả sử rằng (a) các dây vũ trụ có tồn tại, (b) chúng ta có thể tìm ra vị trí và đi tới một dây như thế, (c) chúng ta có thể tìm ra một cách nào đó làm cho nó quay đủ nhanh và (d) một vòng lặp thời gian kín sẽ thật sự hình thành xung quanh nó.
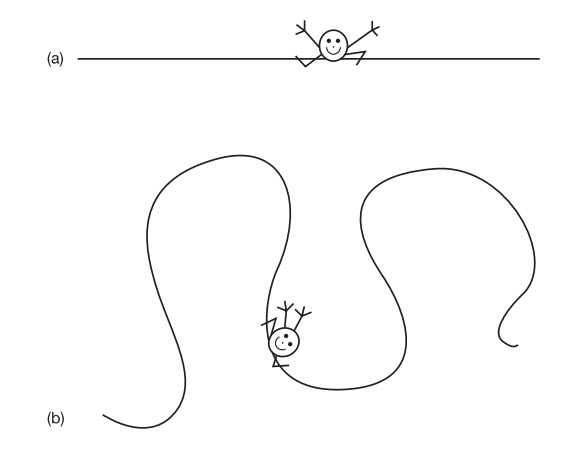
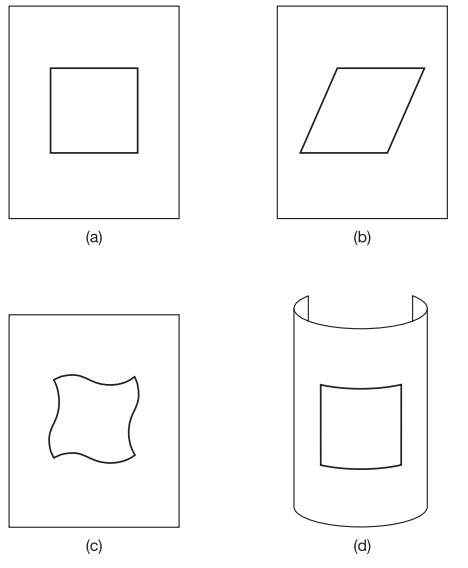
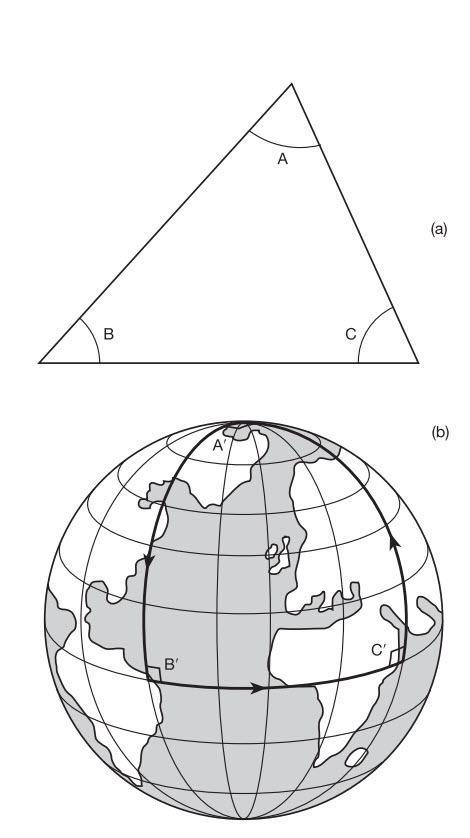
Ngay cả khi một dây vũ trụ không quay tròn, thì không thời gian xung quanh nó cũng bị biến dạng theo một kiểu hơi lạ (vâng, lạ hơn cả không thời gian xung quanh một lỗ đen!). Bất chấp mật độ cao của dây, bạn sẽ không cảm thấy lực hút hấp dẫn cho dù bạn ở gần sợi dây, và không thời gian được nói là phẳng. Tuy nhiên, không gian tự nó sẽ uốn thành hình nón xung quanh sợi dây. Để hình dung, hãy xét một không gian 2D cho đơn giản và một miếng tròn của không gian này xung quanh sợi dây. Nó giống như là một cái nêm không gian đã bị lấy ra như trong hình 9.1(a) và hai rìa bên dán lại với nhau như trong hình 9.1(b). Như vậy sẽ làm cho không gian khép lại vòng quanh dây vũ trụ theo hình nón. Thông thường, chu vi của một vòng tròn bằng hai lần bán kính của nó nhân với pi. Và như vậy, nếu thiếu một miếng tròn, thì chu vi của nó sẽ nhỏ hơn với bán kính như cũ. Nếu bạn đi trong một vòng tròn có bán kính cho trước xung quanh sợi dây thì bạn sẽ thấy quãng đường bạn đi hết vòng tròn và trở lại điểm xuất phát của bạn sẽ ngắn hơn quãng đường bạn đi hết một vòng tròn có cùng bán kính trong không gian bình thường (ở xa dây vũ trụ). Lưu ý rằng sợi dây vũ trụ được mô tả bằng một điểm 0D trong không gian 2D. Thật ra nó là một đường 1D trong không gian 3D (cái tôi không có khả năng trình bày ra ở đây vì tôi không thể nào vẽ một hình nón 4D!).
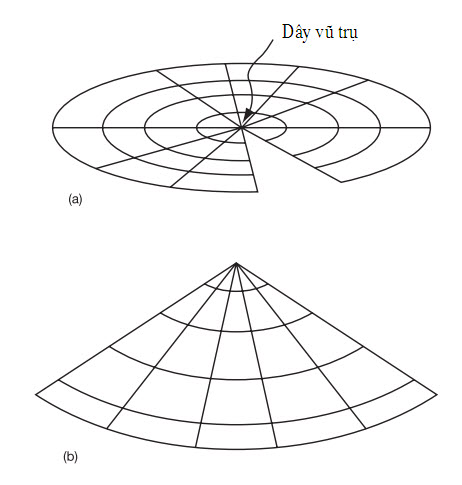
Hình 9.1 Để mô phỏng không gian 3D trông như thế nào ở gần một dây vũ trụ (một đường 1D), ta hãy vứt đi một chiều không gian và xét không gian 2D xung quanh một điểm (0D). Nếu miếng nêm không gian bị lấy khỏi như trong hình (a) và hai rìa dán lại với nhau như trong hình (b) thì không gian sẽ có hình nón.
Một biến thể trên kế hoạch dây vũ trụ này được Richard Gott đề xuất vào năm 1991. Ông đưa ra một cách giải quyết vấn đề cần có dây vũ trụ quay tròn. Thay vậy, ông chỉ rõ làm thế nào hai dây vũ trụ đang chuyển động qua nhau ở tốc độ cao sẽ có hiệu ứng giống như vậy, và một vòng lặp thời gian sẽ hình thành xung quanh cặp dây đó. Vấn đề ở đây là hai sợi dây sẽ phải song song với nhau khi chúng đi qua nhau. Vì thế, cho dù dây vũ trụ có thật sự tồn tại đi nữa, thì chúng ta vẫn sẽ phải hi vọng có hai sợi dây vừa vặn đi qua nhau ở đúng góc độ thích hợp. Gott trình bày rằng chúng ta không cần chờ có hai dây dài vô hạn đi qua nhau. Hiệu ứng tương tự có thể thu được nếu một dây vũ trụ kín, tạo ra một vòng lặp, nó có hình ôvan chứ không tròn (giống như hình dạng tạo bởi một sợi dây cao sau bị kéo căng) co lại sao cho hai phần dài vừa vặn sớt qua khi chúng bay qua nhau. Chính Gott trình bày rằng bất kì vòng lặp thời gian kín nào có thể hình thành xung quanh hai mảnh dây vũ trụ không có chiều dài vô hạn sẽ tạo ra một lỗ đen và bị chắn với bên ngoài bởi chân trời sự kiện, tất nhiên điều đó cũng có nghĩa là chúng không bao giờ có thể khai thác được.
Thật không may, cách thu được một vòng lặp thời gian của Gott còn hại não hơn cả những kế hoạch khác đã có vì, cùng với tất cả những cái nếu và cái nhưng mà tôi vừa nhắc tới, nó đòi hỏi phần khối lượng tổng của các dây phải là cái gọi là “ảo”.2
___________
2Yêu cầu này thậm chí còn tệ hơn cả việc có khối lượng âm, cái đã khó hiểu lắm rồi. Từ ảo hàm ý việc có một tính chất toán học nhất định liên quan đến căn bậc hai của một số âm. Nếu bạn chưa từng gặp loại phép toán này trước đây thì sau đây tôi xin giải thích một chút ngắn gọn. Bạn biết rằng bình phương của một số dương là một số dương, và bình phương của một số âm cũng là một số dương (vì – × – = +). Nhưng một số khi nhân với chính nó vẫn cho một số âm thì được gọi là số ảo vì nó không giống như số (thực) bình thường và có tập hợp những quy tắc riêng của nó. Những con số ảo như vậy có ích trong nhiều lĩnh vực vật lí và kĩ thuật.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili
Bản dịch của Thuvienvatly.com
Phần tiếp theo >>