Giải SBT Vật lý 11 KNTT Mô tả sóng có đáp án. Giải SBT Vật lý 11 KNTT Mô tả sóng có đáp án
Để download tài liệu Giải SBT Vật lý 11 KNTT Mô tả sóng có đáp án các bạn click vào nút TẢI VỀ bên trên.
📅 Ngày tải lên: 20/10/2024
📥 Tên file: giai sbt vat ly 11 kntt mo ta song co dap an-55437-thuvienvatly.doc (425KB)
🔑 Chủ đề: giai sbt vat ly 11 kntt mo ta song co dap an
Giải SBT Vật lý 11 KNTT Mô tả sóng có đáp án
Câu 1: 
Vào một thời điểm Hình 8.1. là đồ thị li độ - quãng đường truyền sóng của một sóng hình sin. Biên độ và bước sóng của sóng này là
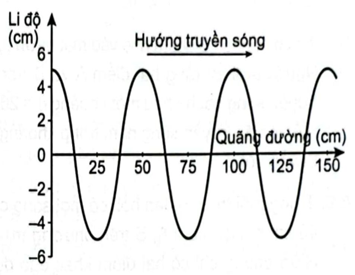
Hình 8.1.
A. \(5{\rm{\;cm}};50{\rm{\;cm}}\).
B. \(6{\rm{\;cm}};50{\rm{\;cm}}\).
C. \(5{\rm{\;cm}};30{\rm{\;cm}}\).
D. \(6{\rm{\;cm}};30{\rm{\;cm}}\).
Câu 2: 
Hình 8.2 là đồ thị li độ - thời gian của một sóng hình sin. Biết tốc độ truyền sóng là \(50{\rm{\;cm}}/{\rm{s}}\). Biên độ và bước sóng của sóng này là
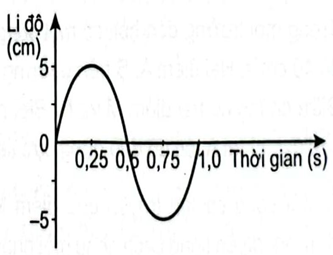
Hình 8.2.
A. \(5{\rm{\;cm}};50{\rm{\;cm}}\).
B. \(10{\rm{\;cm}};0,5{\rm{\;m}}\).
C. \(5{\rm{\;cm}};0,25{\rm{\;m}}\).
D. \(10{\rm{\;cm}};1{\rm{\;m}}\).
Câu 3:
Tại một điểm \({\rm{O}}\) trên mặt nước có một nguồn dao động điều hoà theo phương thẳng đứng với tần số \(2{\rm{\;Hz}}\). Từ điểm \({\rm{O}}\) có những gợn sóng tròn lan rộng ra xung quanh. Khoảng cách giữa hai gợn sóng kế tiếp là \(20{\rm{\;cm}}\). Tốc độ truyền sóng trên mặt nước là
A. \(20{\rm{\;cm}}/{\rm{s}}\).
B. \(40{\rm{\;cm}}/{\rm{s}}\).
C. 80 cm/s.
D. 120cm/s
Câu 4:
Một sóng có tần số \(120{\rm{\;Hz}}\) truyền trong một môi trường với tốc độ \(60{\rm{\;m}}/{\rm{s}}\). Bước sóng của nó là
A. \(1,0{\rm{\;m}}\).
B. \(2,0{\rm{\;m}}\).
C. \(0,5{\rm{\;m}}\).
D. \(0,25{\rm{\;m}}\).
Câu 5:
Một sóng hình sin lan truyền trên trục \(Ox\). Trên phương truyền sóng, khoảng cách ngắn nhất giữa hai điểm mà các phần tử của môi trường tại điểm đó dao động ngược pha nhau là \(0,4{\rm{\;m}}\). Bước sóng của sóng này là
A. \(0,4{\rm{\;m}}\).
B. \(0,8{\rm{\;m}}\).
C. \(0,4{\rm{\;cm}}\).
D. \(0,8{\rm{\;cm}}\).
Câu 6:
Thời gian kể từ khi ngọn sóng thứ nhất đến ngọn sóng thứ sáu đi qua trước mặt một người quan sát là \(12{\rm{\;s}}\). Tốc độ truyền sóng là \(2{\rm{\;m}}/{\rm{s}}\). Bước sóng có giá trị là
A. \(4,8{\rm{\;m}}\).
B. \(4{\rm{\;m}}\).
C. \(6{\rm{\;cm}}\).
D. 48 cm.Câu 7:
Một mũi nhọn \(S\) chạm nhẹ vào mặt nước dao động điều hoà với tần số \({\rm{f}} = 40{\rm{\;Hz}}\). Người ta thấy rằng hai điểm \(A\) và \(B\) trên mặt nước cùng nằm trên phương truyền sóng cách nhau một khoảng \({\rm{d}} = 20{\rm{\;cm}}\) luôn dao động ngược pha nhau. Biết tốc độ truyền sóng nằm trong khoảng từ \(3{\rm{\;m}}/{\rm{s}}\) đến \(5{\rm{\;m}}/{\rm{s}}\). Xác định tốc độ truyền sóng.
Câu 8:
Trong môi trường đàn hồi, có một sóng cơ tần số \(10{\rm{\;Hz}}\) lan truyền với tốc độ \(40{\rm{\;cm}}/{\rm{s}}\). Hai điểm \(A,B\) trên phương truyền sóng dao động cùng pha nhau. Giữa chúng chỉ có hai điểm khác dao động ngược pha với \(A\). Tính khoảng cách \(AB\).
Câu 9:
Trong môi trường đàn hồi, có một sóng cơ có tần số \(10{\rm{\;Hz}}\) lan truyền với tốc độ \(40{\rm{\;cm}}/{\rm{s}}\). Hai điểm \(A,B\) trên phương truyền sóng dao động cùng pha nhau. Giữa chúng có hai điểm \({\rm{M}}\) và \({\rm{N}}\). Biết rằng khi \({\rm{M}}\) hoặc \({\rm{N}}\) có tốc độ dao động cực đại thì tại \({\rm{A}}\) tốc độ dao động cực tiểu. Tính khoảng cách \({\rm{AB}}.\)
Câu 10:
Một sóng cơ lan truyền qua điểm \({\rm{M}}\) rồi đến điểm \({\rm{N}}\) cùng nằm trên một phương truyền sóng cách nhau một phần ba bước sóng. Tại thời điểm \({\rm{t}} = 0\) li độ tại \({\rm{M}}\) là \( + 4{\rm{\;cm}}\) và tại \({\rm{N}}\) là \( - 4{\rm{\;cm}}\). Xác định thời điểm \({{\rm{t}}_1}\) và \({{\rm{t}}_2}\) gần nhất để \({\rm{M}}\) và \({\rm{N}}\) lên đến vị trí cao nhất. Biết chu kì sóng là \(T = 1{\rm{\;s}}\).
Câu 11:
Trên mặt thoáng của một chất lỏng, một mũi nhọn \(O\) chạm vào mặt thoáng dao động điều hoà với tần số \(f\), tạo thành sóng trên mặt thoáng với bước sóng \(\lambda \). Xét hai phương truyền sóng \(Ox\) và \(Oy\) vuông góc với nhau. Gọi \({\rm{M}}\) là một điểm thuộc Ox cách O một đoạn \(16\,\lambda \)và N thuộc Oy cách O một đoạn \(12\,\lambda \). Tính số điểm dao động đồng pha với nguồn \({\rm{O}}\) trên đoạn \({\rm{MN}}\) (không kể \({\rm{M}},{\rm{N}}\)).
