Câu hỏi
🗣️ Ngô Thị Dũng hỏi: Cho mình hỏi một câu Vật lý Lớp 11 trong sách bài tập Sách Kết Nối Tri Thức
Một sóng cơ lan truyền qua điểm \({\rm{M}}\) rồi đến điểm \({\rm{N}}\) cùng nằm trên một phương truyền sóng cách nhau một phần ba bước sóng. Tại thời điểm \({\rm{t}} = 0\) li độ tại \({\rm{M}}\) là \( + 4{\rm{\;cm}}\) và tại \({\rm{N}}\) là \( - 4{\rm{\;cm}}\). Xác định thời điểm \({{\rm{t}}_1}\) và \({{\rm{t}}_2}\) gần nhất để \({\rm{M}}\) và \({\rm{N}}\) lên đến vị trí cao nhất. Biết chu kì sóng là \(T = 1{\rm{\;s}}\).
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: Vat Ly lop 11,trac nghiem.
Câu trả lời hay nhất
🕵 Bạn Phạm Hậu Phú trả lời:
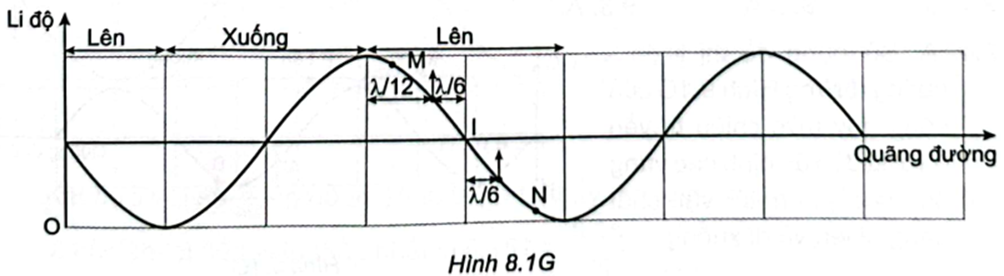
Sử dụng đồ thị li độ - quãng đường Hình 8.1G của sóng quy ước chiều truyền dương để xác định các vùng mà các phần tử vật chất đang đi lên và đi xuống. Li độ Vì sóng truyền qua M rồi mới đến N, nên M ở bên trái và N ở bên phải, mặt khác vì \({u_M} = + 4{\rm{\;cm}}\) và \({u_N} = - 4{\rm{\;cm}}\) , nên chúng phải nằm ở vị trí như Hình 8.1G (cả M và N đều đang đi lên). Vì M cách đỉnh gần nhất một khoảng là \(\frac{\lambda }{{12}}\) nên thời gian ngắn nhất để M đi từ vị trí hiện tại đến vị trí cao nhất là \({t_1} = \frac{T}{{12}} = \frac{1}{{12}}{\rm{\;s}}\) . Tương tự ta xác định được, thời gian ngắn nhất để N đến vị trí cân bằng là \(\frac{T}{6}\) và thời gian ngắn nhất để đi từ vị trí cân bằng đến vị trí cao nhất là \(\frac{T}{4}\) nên \({{\rm{t}}_2} = \frac{{\rm{T}}}{6} + \frac{{\rm{T}}}{4} = \frac{{5{\rm{\;T}}}}{{12}} = \frac{5}{{12}}{\rm{\;s}}\) .
Câu trước | Câu kế tiếp
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Trắc nghiêm chương 2 lớp 11 (.doc)
- TỔNG HỢP TOÀN BỘ LÍ THUYẾT + BÀI TẬP + TRẮC NGHIỆM LỚP 11 (.doc)
- Chắt lọc tinh túy các dạng BT trắc nghiệm lớp 11 (.pdf)
- Bài tập trắc nghiệm Chương cảm ứng điện từ lớp 11 (.doc)
- Trắc nghiệm theo từng chuyên đề lớp 11 (.rar)
- TRẮC NGHIỆM VẬT LÝ LỚP 11 (.rar)
- Sống cùng một vì sao (Phần 2)
- Sống cùng một vì sao (Phần 1)
