3.1 Giới thiệu
Có ba câu chuyện được kể lại. Chuyện thứ nhất kể Galileo là một nhà triết học tự nhiên. Không giống Tycho Brahe và Kepler, Galileo là nhà vật lí thực nghiệm có mối bận tâm hàng đầu là tìm hiểu các định luật của tự nhiên bằng các kĩ thuật định lượng, từ những bài viết xưa nhất của ông cho đến tập chuyên luận để đời sau cùng của ông, Đàm luận và Chứng minh Toán học về Hai Hệ thống Khoa học. Câu chuyện thứ hai thuộc về thiên văn học, và chiếm một thời kì tương đối ngắn, nhưng quan trọng, trong sự nghiệp của ông từ năm 1609 đến 1612, khi những khám phá thiên văn của ông có sức tác động quốc tế ngay tức thì.
Câu chuyện thứ ba kể việc ông bị xét xử và bị quản thúc tại gia sau đó. Các phương diện khoa học mà Tòa án Dị giáo đưa ra để chỉ trích và xét xử ông nằm ngay tại trái tim bản chất của khoa học vật chất. Quan điểm chung của mọi người là xem Galileo như người anh hùng và Giáo hội Thiên Chúa là kẻ thủ ác, là căn nguyên của phản ứng bảo thủ và chính sách hẹp hòi. Từ quan điểm thần học, Galileo đã phạm một sai lầm logic, song giới chức giáo hội còn phạm sai lầm nghiêm trọng hơn, vấn đề được nhắc đi nhắc lại xuyên suốt lịch sử khoa học kể từ đó. Những sai lầm của giáo hội chỉ được chính thức thừa nhận bởi Giáo hoàng John Paul II vào năm 1992.1
Lí do tôi dành cả một chương cho Galileo, nền khoa học và những khổ cực của ông một phần là do thực tế trường hợp này nên được hiểu rõ hơn, song điều quan trọng hơn, vì câu chuyện này phản ánh được cách thức vật lí được thực hiện với tư cách một bộ môn khoa học. Tính chính trực và tài năng khoa học của Galileo là một nguồn cảm hứng – hơn bất kì ai khác, ông có thể được vinh danh với việc sáng tạo ra khuôn khổ trí óc cho nghiên cứu vật lí như chúng ta biết ngày nay.
3.2 Galileo là nhà vật lí thực nghiệm
Galileo Galilei chào đời vào tháng Hai 1564 ở Pisa, là con trai của Vincenzio Galileo, một nhạc sĩ và nhà lí thuyết âm nhạc có tiếng. Vào năm 1587, Galileo được bổ nhiệm chức danh giáo sư toán tại Đại học Pisa, nơi ông chẳng mấy mặn mòi với các đồng nghiệp, một trong những lí do chính là vì ông phản đối vật lí học Aristotle khi ấy vẫn là trụ cột trung tâm của triết học tự nhiên. Galileo thấy rõ rằng vật lí học Aristotle không phù hợp với cách thức vật chất hành xử trên thực tế. Ví dụ, phần khẳng định về chuyển động của các vật rơi có trọng lượng khác nhau đọc như sau:
Giả sử một vật nặng nhất định đi được một quãng đường nhất định trong một thời gian nhất định, vật nặng hơn sẽ đi được cùng một quãng đường trong thời gian ngắn hơn, và tỉ lệ trọng lượng của các vật bằng bao nhiêu thì tỉ lệ thời gian sẽ bằng bấy nhiêu; chẳng hạn, giả sử một nửa vật đi hết quãng đường trong thời gian x, thì nguyên vật sẽ đi hết quãng đường đó trong thời gian x/2.2
Điều này rõ ràng là sai, và có thể được chứng minh bằng một thí nghiệm đơn giản. Phản đối của Galileo được hình tượng hóa bởi câu chuyện ông thả rơi các vật nặng khác nhau từ đỉnh Tháp nghiêng Pisa. Nếu chúng được thả rơi từ cùng một độ cao, thì chúng chạm đất cùng lúc, nếu bỏ qua sức cản không khí, đúng như Galileo và các tác giả trước đó đã biết.
Vào năm 1592, Galileo được bổ nhiệm chức giáo sư toán tại Padua, nơi ông ở lại làm việc cho đến năm 1610. Trong quãng thời gian này ông đã sáng tạo một số công trình kiệt xuất nhất của mình. Ban đầu ông phản đối mô hình Copernicus về Hệ Mặt Trời nhưng, vào năm 1595, ông bắt đầu xem xét nó một cách nghiêm túc để giải thích nguồn gốc của thủy triều ở biển Adriatic. Ông quan sát thấy thủy triều tại Venice thường dâng lên hạ xuống khoảng 5 foot, chừng 1,5 mét, và do đó phải có một lực rất lớn làm cho lượng nước đồ sộ này dâng lên mỗi ngày ở mức triều cao như thế. Galileo lí giải rằng, nếu Trái Đất quay xung quanh trục riêng của nó và đồng thời chuyển động trong quỹ đạo tròn xung quanh Mặt Trời, thì độ biến thiên hướng chuyển động của một điểm trên bề mặt Trái Đất sẽ nén ép xung quanh và vì thế gây ra hiệu ứng thủy triều. Đây không phải lời giải thích đúng cho thủy triều, nhưng nó khiến Galileo ngả về bức tranh Copernicus cho các luận giải vật lí.
Trong những công trình được in của Galileo, các luận cứ được trình bày theo những luận điểm trừu tượng mà không hề tham chiếu đến ý nghĩa thông thường cho bằng chứng thực nghiệm. Tài năng của Galieo với vai trò nhà khoa học tiên phong được miêu tả bởi Stillman Drake trong quyển sách đáng chú ý của ông, Galileo: Nhà khoa học tiên phong (1990). Drake giải mã các ghi chú chưa được công bố của Galileo và chứng minh một cách thuyết phục rằng Galileo đã thật sự tiến hành các thí nghiệm mà ông nhắc tới trong các chuyên luận của mình với kĩ năng thực nghiệm đáng nể (Hình 3.1).
Nhiệm vụ của Galileo thật khó khăn – ông không tin vào cơ sở của vật lí học Aristotle nhưng lại chẳng có gì khác thay thế cho nó. Vào đầu những năm 1600, ông đã tiến hành các khảo sát thực nghiệm về quy luật của sự rơi, chuyển động của các quả cầu lăn xuống dốc nghiêng và chuyển động của con lắc – những nghiên cứu này đã làm rõ, lần đầu tiên, khái niệm gia tốc.
Một vấn đề đối với vật lí học cho đến thời Galileo là chẳng có cách nào đo chính xác những khoảng thời gian nhỏ, và vì thế ông phải sử dụng biện pháp khéo léo trong thiết kế các thí nghiệm của mình. Một ví dụ đẹp là thí nghiệm của ông khảo sát cách một quả cầu thu gia tốc khi nó lăn xuống một mặt phẳng nghiêng. Ông đã xây dựng một mặt phẳng nghiêng thoai thoải dài 2 mét chỉ hợp góc 1,7o so với phương ngang và xẻ một cái rãnh trên đó để một quả cầu nặng bằng đồng thiếc có thể lăn xuống. Ông đặt những miếng nêm nhỏ lên mặt phẳng nghiêng để cho mỗi khi quả cầu đi qua một miếng nêm thì có một tiếng rắc phát ra. Sau đó ông điều chỉnh vị trí của các miếng nêm sao cho các tiếng rắc đó sẽ phát ra sau những khoảng thời gian bằng nhau (Hình 3.2). Drake đề xuất rằng Galileo có thể cân bằng các khoảng thời gian đến 1/64 giây bằng cách ngân một giai điệu và làm cho những tiếng rắc đó phát ra đúng nhịp bài hát. Bằng cách lấy hiệu, ông tính được tốc độ trung bình giữa những tiếng rắc liên tiếp và tìm thấy nó tăng lên theo các số lẻ 1,3, 5,7,… trong những khoảng thời gian bằng nhau.

Hình 3.1 Một phần ghi chú của Galileo về các quy luật của con lắc. (Trích từ S. Drake, 1990. Galileo: Nhà khoa học tiên phong, trang 19, Toronto, NXB Đại học Toronto.)
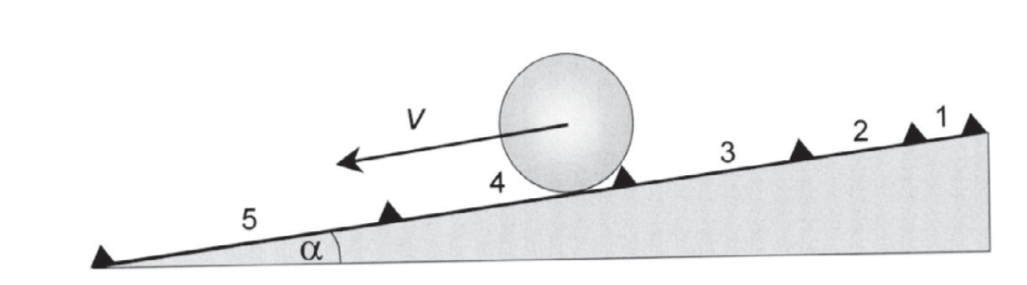
Hình 3.2 Cách Galileo thiết lập quy luật về chuyển động dưới gia tốc không đổi. Con số giữa các miếng nêm thể hiện vị trí tương đối của chúng để tạo ra chuỗi tiếng rắc đều đặn.
Ban đầu, Galileo tin rằng, dưới gia tốc không đổi, tốc độ tỉ lệ thuận với quãng đường đi được nhưng, từ các kết quả thí nghiệm của ông vào năm 1604, ông tìm thấy đúng hơn thì tốc độ tỉ lệ thuận với thời gian. Bây giờ ông có hai liên hệ: thứ nhất là liên hệ giữa tốc độ và quãng đường, x = vt đối với vận tốc không đổi v, và thứ hai liên hệ tốc độ với thời gian dưới gia tốc không đổi v = at. Không có biểu thức đại số nào trong các công trình của Galileo và giải tích vi phân vẫn chưa được khám phá. Thủ tục đơn giản nhất là chia nhỏ bài toán thành những khoảng thời gian hữu hạn. Giả sử tốc độ của quả cầu gia tốc đều ấy được đo tại các thời điểm 0, 1, 2, 3, 4, 5,… s, giả sử nó bắt đầu từ trạng thái nghỉ lúc t = 0. Gia tốc là không đổi và vì thế tốc độ tại những thời điểm này, ví dụ bằng 0, 1, 2, 3, 4…,
cm s-1, thì gia tốc a = 1 cm s-2. Hạt đi được quãng đường bao xa sau 0, 1, 2, 3, 4, 5,… s?
Lúc t = 0, hạt chưa được đi quãng đường nào. Giữa 0 và 1 s, tốc độ trung bình là
0,5 cm s-1, và vì thế quãng đường đi được là 0,5 cm. Trong khoảng thời gian tiếp theo giữa 1 và 2 s, tốc độ trung bình là 1,5 cm s-1 và vì thế quãng đường đi được trong khoảng thời gian đó là 1,5 cm và tổng quãng đường đi được tính từ lúc đứng yên là 0,5 + 1,5 = 2 cm. Trong khoảng thời gian tiếp theo, tốc độ trung bình là 2,5 cm s-1, quãng đường đi được là 2,5 cm và tổng quãng đường là 4,5 cm, và cứ thế. Ta thu được chuỗi quãng đường 0; 0,5; 2; 4,5; 8; 12,5;… cm có thể viết dưới dạng

Kết quả này đại diện cho một cuộc cách mạng trong tư duy về bản chất của chuyển động có gia tốc và đã dẫn tới cuộc cách mạng Newton.
Ông không dừng lại ở đây mà tiếp tục tiến hành các thí nghiệm then chốt khác. Tiếp theo ông nghiên cứu về quy luật của sự rơi, cụ thể là, nếu một vật được thả rơi từ những độ cao khác nhau, thì nó mất bao nhiêu thời gian để chạm đất? Ông sử dụng một hình thức đồng hồ nước để đo các khoảng thời gian một cách chính xác. Nước được chép chảy ra khỏi một ống dẫn ở dưới đáy một cái bình lớn sao cho lượng nước chảy ra là một số đo về khoảng thời gian. Bằng cách thả rơi các vật từ những độ cao khác nhau, ông xác định được rằng vật rơi tuân theo quy tắc thời gian bình phương – nói cách khác, khi vật rơi tự do, chúng chịu một gia tốc không đổi, tức là gia tốc trọng trường.
Xác định được hai kết quả này, ông đi tìm mối liên hệ giữa chúng – câu trả lời là định lí Galileo. Giả sử một quả cầu được thả rơi tự do qua một quãng đường nhất định l, nó được biểu diễn bằng độ dài AB trên Hình 3.3. Dựng một đường tròn có đường kính bằng độ dài l đã cho. Bây giờ giả sử quả cầu trượt không ma sát xuống mặt phẳng nghiêng AC và, để cho tiện, đỉnh của mặt phẳng nghiêng trùng tại điểm A. Định lí Galileo phát biểu như sau:
Thời gian để quả cầu trượt xuống mặt phẳng nghiêng từ A đến điểm C, nơi mặt phẳng nghiêng cắt qua đường tròn, bằng với thời gian để quả cầu rơi tự do từ A đến B.
Nói cách khác, thời gian để một vật rơi theo một dây cung bất kì bằng với thời gian để nó rơi thẳng đứng xuyên đường kính của đường tròn. Khi quả cầu trượt xuống mặt phẳng nghiêng, thành phần gia tốc trọng trường gsina tác dụng lên nó, phần còn lại của gia tốc trọng trường được cân bằng bởi phản lực của mặt phẳng nghiêng (Hình 3.3). Thế nhưng, theo hình học, một tam giác bất kì dựng trên đường kính của một đường tròn, điểm thứ ba nằm trên đường tròn, là một tam giác vuông. Do đó, ta có thể cho các góc bằng nhau như trên Hình 3.3, từ hình vẽ ta thấy rõ AC/AB = sina, tỉ số các quãng đường đi được. Vì quãng đường đi được tỉ lệ với gia tốc, x = ½ at2, nên điều này chứng minh định lí Galileo.
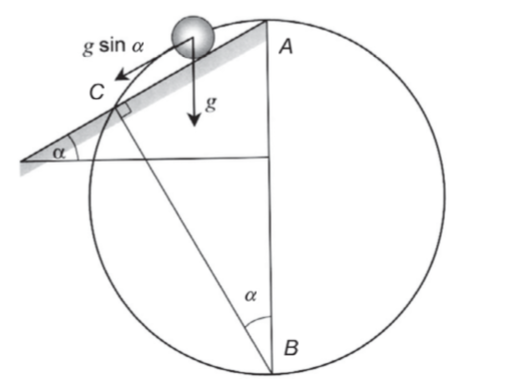
Hình 3.3 Cách Galileo thiết lập định lí Galileo.
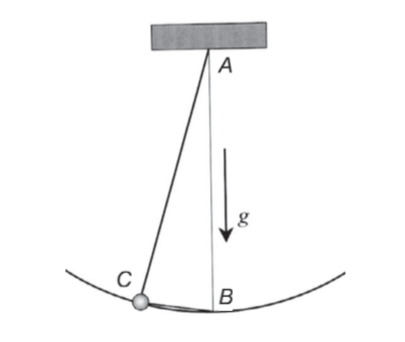
Hình 3.4 Cách Galileo chỉ ra rằng chu kì của một con lắc dài là độc lập với biên độ dao động.
Sau đó, Galileo nhận ra mối liên hệ giữa những hiện tượng này và tính chất của các con lắc dao động. Người ta kể rằng, lúc còn trẻ ông từng để ý thấy chu kì đong đưa của đèn treo nhiều ngọn trong nhà thờ là độc lập với biên độ dao động. Galileo đã sử dụng quy tắc dây cung của ông để giải thích quan sát này. Nếu con lắc đủ dài, thì cung tròn được con lắc vạch ra hầu như bằng với dây cung nối điểm biên của con lắc với điểm thấp nhất của nó (Hình 3.4). Do đó, ta rõ ràng thấy được chu kì của con lắc độc lập với biên độ dao động của nó – theo định lí Galileo, thời gian đi theo một dây cung bất kì vẽ từ B luôn bằng thời gian để vật rơi tự do xuống hai lần độ dài của con lắc, như ta có thể thấy trên Hình 3.3.
Cái Galileo thu được là đưa bản chất của gia tốc trọng trường vào hình thức toán học. Việc này có ứng dụng thực tiễn ngay tức thì vì lúc này ông có thể tính được quỹ đạo của các vật bị ném. Chúng chuyển động với tốc độ không đổi theo phương song song với mặt đất và bị giảm tốc bởi trọng lực theo phương thẳng đứng. Lần đầu tiên, ông đã có thể chỉ ra quỹ đạo parabol của đạn pháo và những vật bị ném khác (Hình 3.5).
Galileo bắt đầu viết một bài khảo cứu có hệ thống về những chủ đề này, chỉ ra cách hiểu chúng trên cơ sở quy tắc gia tốc không đổi. Vào năm 1610, ông lên kế hoạch viết:
Ba quyển sách về cơ học, hai quyển chứng minh các nguyên lí của nó, và một quyển nói về những vấn đề của nó; và mặc dù có tác giả khác đã viết về chủ đề này, nhưng cái họ làm được chưa tới một phần tư những gì tôi viết, dù xét theo số lượng hay bất kì tiêu chí nào khác.4
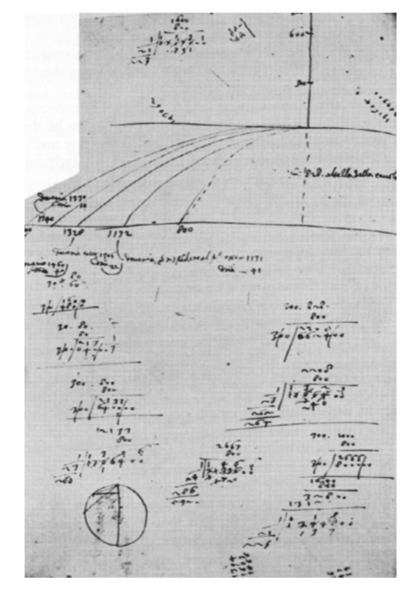
Hình 3.5 Một trang trích từ sổ ghi chép của Galileo trình bày quỹ đạo của các vật bị ném dưới sự kết hợp của gia tốc trọng trường và tốc độ phương ngang không đổi. (Trích từ S. Drake, 1990. Galileo: Nhà khoa học tiên phong, trang 107. Toronto, NXB Đại học Toronto.)
Về sau, ông viết với giọng điệu giống như vậy:
Ba quyển sách về chuyển động cục bộ – một khoa học hoàn toàn mới trong đó chưa có người nào khác, dù xưa hay hiện đại, từng khám phá được chút nào trong những định luật đáng chú ý nhất mà tôi chứng minh là tồn tại trong chuyển động tự nhiên lẫn chuyển động cưỡng bức; vì thế tôi có thể gọi đây là một khoa học mới và là một khoa học được tôi khám phá từ những nền tảng cốt lõi nhất của nó.5
Ông trệch hướng khỏi nhiệm vụ này do bởi tin tức lan tới về phát minh kính thiên văn, sự kiện này đánh dấu việc ông bắt đầu nghiên cứu thiên văn học một cách nghiêm túc. Sau đó, ông bị xét xử vào năm 1615 – 16. Bởi thế, việc xuất bản các khám phá của Galileo bị hoãn lại cho đến thập niên 1620 và 1630.
3.3 Những khám phá thiên văn của Galileo
Phát minh kính thiên văn được quy cho người thợ mài kính người Hà Lan Hans Lipperhey, vào tháng Mười 1608 ông xin Công tước Maurice xứ Nassau cấp bằng sáng chế cho một dụng cụ có thể khiến những vật ở xa trông gần hơn, nhưng không được chấp thuận. Galileo nghe nói tới phát minh này vào tháng Bảy 1609 và bắt tay vào tự chế tạo một chiếc. Vào tháng Tám, ông đạt được độ phóng đại 9 lần, tốt hơn ba lần so với kính thiên văn của Lipperhey. Điều này gây ấn tượng rất lớn đối với Thượng viện Venice, họ hiểu rõ tầm quan trọng quân sự của một dụng cụ như thế đối với một quốc gia ven biển. Galileo lập tức được bổ nhiệm một chức danh trọn đời tại Đại học Padua và được tăng lương nhanh chóng.
Vào cuối năm 1609, Galileo đã chế tạo được một số kính thiên văn có độ phóng đại tăng dần, đỉnh điểm có số phóng đại 30. Vào tháng Một 1610, lần đầu tiên ông hướng kính thiên văn của mình lên bầu trời và lập tức xuất hiện cả một đợt lũ khám phá nổi bật. Những khám phá này nhanh chóng được công bố vào tháng Ba 1610 trong công trình Sidereus Nuncius hay Người đưa tin Thiên văn của ông.6 Nói tóm lược, những khám phá này bao gồm:
(1) Mặt Trăng có địa hình núi non chứ không phải một quả cầu hoàn toàn trơn tru (Hình 3.6a).
(2) Dải Ngân Hà gồm vô số sao chứ không phải một phân bố đều của ánh sáng (Hình 3.6b).
(3) Mộc tinh có bốn vệ tinh và chuyển động của chúng được theo dõi trong khoảng thời gian gần hai tháng, cho phép xác định được chu kì quỹ đạo của chúng (Hình 2.9).
Quyển sách gây chú ý trên khắp châu Âu và Galileo lập tức có danh tiếng quốc tế. Những khám phá này đã đánh đổ một số giáo điều Aristotle từng được chấp nhận trong hàng thế kỉ. Ví dụ, sự phân giải Dải Ngân Hà thành từng sao là đi ngược lại với quan điểm Aristotle. Ở các vệ tinh của Mộc tinh, Galileo nhìn thấy một nguyên mẫu cho bức tranh Copernicus về Hệ Mặt Trời. Tác dụng ngay tức thì của những khám phá này là việc Galileo được công nhận là nhà toán học và nhà triết học bởi Đại công tước Tuscany, Cosimo de Medici, người được đề tặng ở quyển Sidereus Nuncius.
Về cuối năm 1610, ông thực hiện hai khám phá thiên văn chủ chốt khác:
(4) các vành sao Thổ, ông xem chúng gần như là vệ tinh của hành tinh này;
(5) các pha của Kim tinh.
Khám phá Kim tinh này có tầm quan trọng lớn nhất. Với chiếc kính thiên văn của ông, Galileo đã có thể phân giải đĩa Kim tinh và quan sát sự rọi sáng của nó do Mặt Trời. Khi Kim tinh ở phía bên kia quỹ đạo của nó so với Trái Đất, cái đĩa xuất hiện có dạng tròn, nhưng khi nó ở cùng phía so với Mặt Trời giống Trái Đất, cái đĩa trông giống như trăng lưỡi liềm. Điều này được xem là bằng chứng nghiêng về bức tranh Copernicus vì nó tìm được một lời giải thích tự nhiên nếu Kim tinh và Trái Đất đều quay xung quanh Mặt Trời, nguồn gốc rọi sáng của chúng (Hình 3.7b). Mặt khác, nếu Kim tinh chuyển động trong một ngoại luân xung quanh một quỹ đạo tròn xung quanh Trái Đất và Mặt Trời chuyển động trên một quả cầu ở xa hơn, thì kiểu rọi sáng so với Trái Đất sẽ hơi khác, như minh họa ở Hình 3.7a. Vào năm 1611, những khám phá này được Galileo trình bày trước Giáo hoàng và một số hồng y, và họ có ấn tượng tích cực với chúng. Galileo được bầu vào Viện hàn lâm Lincei.
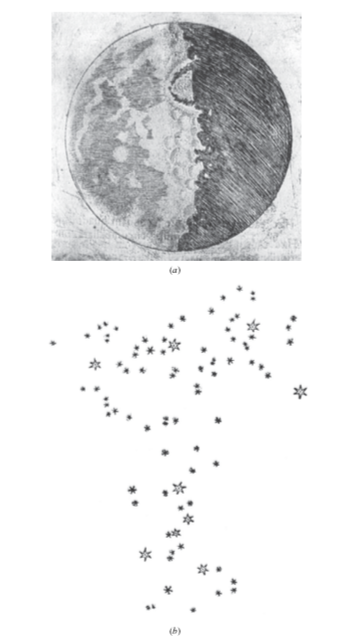
Hình 3.6 (a) Hình vẽ của Galileo về Mặt Trăng như quan sát qua kính thiên văn của ông. Trên thực tế, những miệng hố lớn giao cắt bởi những đường phân chia sáng tối là không có thật. Nên xem đây là hình minh họa. (b) Hình phác thảo của Galileo về vùng trời trong vùng phụ cận thắt lưng của chòm sao Tráng Sĩ, cho thấy sự phân giải phông sáng nền thành những ngôi sao mờ nhạt. (Trích A. van Helden, 1989. Sidereus Nuncius hay Người đưa tin Thiên văn, trang 108. Chicago: NXB Đại học Chicago.)
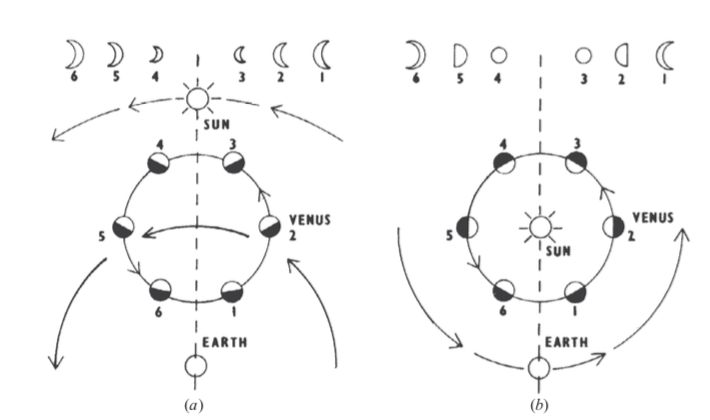
Hình 3.7 Minh họa các pha của Kim tinh, theo bức tranh (a) Địa tâm và (b) Nhật tâm về cấu trúc của Hệ Mặt Trời. (Trích từ G. Galilei, 1610. Sidereus Nuncius, Venice. Xem thêm bản dịch của A. van Helden, 1989. Chicago: NXB Đại học Chicago.)
3.4 Vật lí học Aristotle và vật lí học Galileo: Trái tim của vật chất
Trước khi thuật lại những sự kiện dẫn tới sự trình diện của Galileo vào năm 1632 trước Tòa án Dị giáo và việc luận tội ông là tội phạm nguy hiểm vào hàng thứ hai trong hệ thống xét xử thuộc Giáo hội, ta hãy tóm tắt một số mặt tranh luận giữa học thuyết Ptolemy, học thuyết Copernicus và chính quyền giáo hội. Finocchiaro cung cấp một bản tóm tắt tuyệt vời trong tư liệu lịch sử của ông, Vụ án Galileo.7 Những quy luật được chấp nhận của vật lí học vẫn là của Aristotle, và chỉ số ít người có tinh thần phiêu lưu mới nghi ngờ tính đúng đắn của những quy luật này và của hệ thống Ptolemy về thế giới. Tuy nhiên, có một số trục trặc với bức tranh Copernicus, vì thế Galileo phải dính líu với những vấn đề này bởi chúng có khả năng làm xói mòn nhận thức mới thiết lập của ông về các định luật của chuyển động.
3.4.1 Các vấn đề
Các vấn đề vật lí tập trung vào những câu hỏi sau: (i) Trái Đất có quay xung quanh trục của nó so với các sao cố định hay không, và (ii) Trái Đất và các hành tinh có quay xung quanh Mặt Trời không? Đặc biệt, Trái Đất có chuyển động hay không? Khái niệm vừa đề cập này được gọi là giả thuyết địa động. Finocchiaro tóm tắt các luận điểm của phe triết học Aristotle dưới năm đề mục:
(1) Sự lừa dối của các giác quan. Không có giác quan nào của chúng ta đem lại bất kì bằng chứng nào rằng Trái Đất đang chuyển động trong một quỹ đạo xung quanh Mặt Trời. Nếu đây là một sự thật về tự nhiên, thì chắc chắn nó sẽ có tầm quan trọng đến mức các giác quan của chúng ta sẽ khiến chúng ta nhận thức về nó.
(2) Các vấn đề thiên văn. Thứ nhất, những vật thể trên trời được cho là được cấu tạo bởi những dạng vật chất khác với vật vật chất trên Trái Đất. Thứ hai, Kim tinh phải biểu hiện các pha giống như Mặt Trăng nếu nó chuyển động trong một quỹ đạo xung quanh Mặt Trời. Thứ ba, nếu Trái Đất chuyển động, vậy tại sao các sao không biểu hiện thị sai?
(3) Các luận điểm vật lí. Các luận điểm này dựa trên vật lí học Aristotle và một số đã được bàn luận.
(a) Nếu Trái Đất chuyển động thì các vật rơi sẽ không rơi thẳng đứng. Có thể nêu ra nhiều ví dụ phản bác – mưa rơi thẳng đứng, các vật bị ném lên thẳng đứng rơi thẳng xuống trở lại, và vân vân. Điều này trái ngược với quỹ đạo của một vật được thả rơi từ đỉnh cột buồm của một con tàu đang chuyển động. Trong trường hợp này, vật không rơi thẳng đứng xuống dưới.
(b) Những vật bị ném theo hướng quay của Trái Đất và theo hướng ngược lại phải có quỹ đạo khác nhau. Chưa có khác biệt nào được quan sát thấy.
(c) Những vật đặt trên bánh xe quay của người thợ gốm bị văng ra nếu chúng không được giữ lại, đây là thứ được gọi là Sức mạnh Tống khứ của Chuyển động xoáy – ngày nay chúng ta gọi đây là lực li tâm. Hiện tượng tương tự phải xảy ra nếu Trái Đất ở trạng thái chuyển động quay, thế nhưng chúng ta không bị văng ra khỏi mặt đất.
(d) Tiếp theo, có những lập luận thuần túy lí thuyết. Theo vật lí học Aristotle, chỉ có hai hình thức chuyển động, chuyển động thẳng đều và chuyển động tròn đều – đây là những chuyển động ‘tự nhiên’ duy nhất. Các vật hoặc là phải rơi theo đường thẳng đến tâm Vũ trụ, hoặc là phải ở trạng thái chuyển động tròn đều. Chúng ta đã bàn luận lập luận cho rằng các vật rơi thẳng về tâm Trái Đất chứ không rơi về phía Mặt Trời. Hơn nữa, theo vật lí học Aristotle, những vật đơn giản chỉ có thể có một chuyển động tự nhiên. Thế nhưng, theo Copernicus, những vật thả rơi trên Trái Đất có ba chuyển động – chuyển động hướng xuống do sự rơi tự do, chuyển động quay của Trái Đất xung quanh trục của nó và chuyển động trong quỹ đạo tròn xung quanh Mặt Trời.
(e) Cuối cùng, nếu vật lí học Aristotle bị bác bỏ, thì cái gì thay thế cho nó? Phe Copernicus phải đưa ra một lí thuyết tốt hơn và chưa lí thuyết nào sẵn có hết.
(4) Uy lực của Kinh thánh. Có những nhận định không hề rõ ràng trong Kinh Thánh khẳng định rằng Trái Đất đứng yên tại trung tâm của Vũ trụ. Theo Finocchiaro, những nhận định có liên quan nhất là như sau:8
(a) Psalm 104:5 ‘Lạy Chúa… người đã thiết lập nền tảng của Trái Đất, rằng nó mãi mãi không bị di dời.’
(b) Ecclesiastes 1:5 ‘Mặt Trời mọc, rồi Mặt Trời lặn, và đi đến nơi nó mọc lên.’
(c) Joshua 10:12, 13 ‘Ngày mà Chúa phó dân Amorite cho dân Israel, thì Joshua thưa cùng Chúa tại Israel rằng: ‘Hỡi Mặt Trời, hãy dừng lại trên Gibeon; hỡi Mặt Trăng, hãy dừng lại trên thung lũng Ajalon’. Và Mặt Trời dừng lại, và Mặt Trăng đứng yên, cho đến khi dân chúng trả thù xong kẻ thù của mình.’
Đây là những tài liệu tham khảo khá thiên lệch và điều thú vị là người Tin Lành chống học thuyết Copernicus còn mạnh mẽ hơn giáo hội Công giáo do bởi niềm tin của họ vào những sự thật theo nghĩa đen trong Kinh Thánh. Các nhà thần học Công giáo có cách giải thích phức tạp hơn và linh hoạt hơn về những gì ghi chép trong Kinh Thánh. Tuy nhiên, quan niệm Trái Đất đứng yên tại trung tâm của Vũ trụ cũng là kết luận của các Giáo Phụ (Church Fathers) – các vị thánh, các nhà thần học và những người trong giáo hội đã làm cho Công giáo trở nên bí ẩn. Trích dẫn Finocchiaro:
Luận điểm ấy tuyên bố rằng tất cả các Giáo Phụ đều nhất trí trong việc giải thích các đoạn Kinh Thánh có liên quan… phù hợp với quan niệm địa tĩnh; vì thế, hệ thống địa tĩnh ràng buộc với mọi tín đồ, và để tuyên bố những gì ngược lại (như Copernicus đã làm) là dị giáo.9
(5) Luận điểm hấp dẫn nhất nhìn từ quan điểm của chúng ta là bản chất giả thuyết của học thuyết Copernicus. Nó đánh vào tận trung tâm bản chất của khoa học tự nhiên. Điểm mấu chốt là cách chúng ta trình bày những nhận định về sự thành công của mô hình Copernicus. Một nhận định đúng là như sau:
Nếu Trái Đất quay quanh trục của nó và chuyển động trong quỹ đạo tròn xung quanh Mặt Trời, và nếu những hành tinh khác cũng chuyển động xung quanh Mặt Trời, thì ta có thể mô tả thật dễ dàng và thật đẹp các chuyển động quan sát thấy của Mặt Trời, Mặt Trăng, và các hành tinh trên thiên cầu.
Cái chúng ta không thể làm theo logic là đảo ngược lập luận trên và nói rằng, vì các chuyển động hành tinh được giải thích thật đơn giản và thật đẹp bởi giả thuyết Copernicus, nên Trái Đất phải quay và chuyển động trong quỹ đạo tròn xung quanh Mặt Trời. Đây là một lỗi logic cơ bản, bởi vì phải có những mô hình khác nữa cũng thành công giống như mô hình Copernicus.
Điểm then chốt là sự khác biệt giữa lập luận quy nạp và diễn dịch. Owen Gingerich cung cấp một ví dụ dễ hiểu.10 Một chuỗi suy luận diễn dịch có thể như sau:
(a) Nếu trời đang mưa, thì đường ướt.
(b) Trời đang mưa.
(c) Do đó, đường ướt.
Không có vấn đề gì ở đây. Thế nhưng, bây giờ hãy đảo ngược (b) và (c) và chúng ta gặp rắc rối:
(a) Nếu trời đang mưa, thì đường ướt.
(b) Đường ướt.
(c) Do đó, trời đang mưa.
Hướng lập luận này rõ ràng là sai, vì con đường có thể là đường phố Venice, hoặc có thể mới được rửa nước. Nói cách khác, bạn không thể chứng minh bất cứ điều gì về tính chân thật tuyệt đối của những nhận định thuộc loại thứ hai này. Kiểu lập luận thứ hai này trong đó chúng ta cố đi tìm những quy luật chung từ những mảnh bằng chứng đặc biệt được gọi là suy luận quy nạp. Toàn bộ các khoa học vật chất đều ít nhiều có mức ‘bản chất giả định’ này. Điều này trái ngược với sự chắc chắn tuyệt đối của những lời Chúa răn được ghi lại trong kinh sách và cách giảng giải của nó dưới dạng giáo điều bởi các Giáo Phụ. Theo Owen Gingerich, đây là vấn đề cốt lõi dẫn tới việc xét xử và buộc tội Galileo – sự gần gũi của bức tranh thế giới giả thuyết của Copernicus với chân lí tuyệt đối được tiết lộ trong Kinh Thánh và được mã hóa bởi các Giáo Phụ.
3.4.2 Vụ án Galileo
Trước khi có những khám phá thiên văn vĩ đại của ông vào năm 1610-11, Galileo vốn cảnh giác cao độ trước học thuyết Copernicus, nhưng dần dần ông cảm thấy hiểu biết mới của mình về bản chất của chuyển động loại trừ được những vấn đề vật lí được nêu ở trên. Bằng chứng mới phù hợp với mô hình Copernicus. Đặc biệt, có núi non trên Mặt Trăng, y hệt như trên Trái Đất, cho thấy Trái Đất và Mặt Trăng là những vật thể giống nhau. Các pha của Kim tinh chính xác như trông đợi theo bức tranh Copernicus. Như vậy, những phản bác vật lí và thiên văn đối với học thuyết Copernicus có thể bị loại trừ, chỉ để lại những vấn đề thần học và logic để tranh luận.
Khi bằng chứng bắt đầu tích góp nghiêng về học thuyết Copernicus, các nhà khoa học và nhà triết học bảo thủ phải dựa vào các luận điểm thần học, triết lí và logic ngày một nhiều hơn. Vào tháng Mười Hai 1613, Nữ đại công tước Dowager Christina đã hỏi Castelli, một người bạn và đồng nghiệp của Galileo, về những phản bác mang tính tôn giáo đối với chuyển động của Trái Đất. Castelli đáp lời thỏa mãn cả Nữ công tước và Galileo, nhưng Galileo cảm thấy cần phải xây dựng các luận điểm chi tiết hơn. Ông đề xuất rằng có ba chỗ sai sót chết người trong các lí lẽ thần học. Trích theo Finocchiaro:
Thứ nhất, nó cố chứng minh một kết luận (sự đứng yên của Trái Đất) trên cơ sở một tiền đề (sự cam chắc của Kinh Thánh về hệ thống địa tĩnh) vốn chỉ có thể biết chắc với kết luận đó ngay từ đầu… Công việc giải thích Kinh Thánh phụ thuộc vào nghiên cứu vật lí, và việc đưa ra một kết luận vật lí gây tranh cãi dựa trên Kinh Thánh chẳng khác nào việc đặt xe kéo phía trước con ngựa cả. Thứ hai, sự phản bác dựa trên Kinh Thánh là không hợp logic, bởi lẽ Kinh Thánh chỉ có giá trị trong các vấn đề đức tin và đạo đức, chứ không phải trong các truy vấn khoa học… Cuối cùng, người ta có thể hỏi liệu chuyển động của Trái Đất có mâu thuẫn với Kinh Thánh hay không.11
Bức thư này được lưu hành riêng tư và đến tay những người bảo thủ. Những buổi thuyết trình được tổ chức nhằm công kích bức tranh nhật tâm và buộc tội những người ủng hộ nó là dị giáo. Vào tháng Ba 1615, Tu sĩ Dòng Tên Tommaso Caccini, người từng rao giảng chống lại Galileo, đưa ra một lời buộc tội chính thức về nghi ngờ dị giáo chống Galileo trước Tòa án Dị giáo La Mã. Lời buộc tội này không đáng sợ bằng tội dị giáo chính thức, song tính chất vẫn nghiêm trọng. Sổ sách Tòa án Dị giáo nói, ‘Tình nghi dị giáo là những kẻ thỉnh thoảng thốt ra những đề xuất làm xúc phạm người nghe… Những kẻ tàng trữ, ghi chép, đọc hoặc chuyền cho người khác đọc những quyển sách cấm trong danh mục…’ Ngoài ra, có hai loại tình nghi dị giáo, tình nghi mức nặng và tình nghi mức nhẹ, mức nặng bị xem là nghiêm trọng hơn mức kia. Một khi bị kết tội, sẽ có một thủ tục chính thức phải tuân theo.
Galileo đáp lại bằng cách tìm kiếm sự hậu thuẫn của bạn bè và người bảo trợ, và bí mật lưu hành ba chuyên luận dài. Một trong số này lặp lại những lí lẽ về giá trị của những luận điểm thần học và được biết tới là thư của Galileo gửi Nữ Đại Công tước Christina; phiên bản hiệu chỉnh được mở rộng từ tám lên bốn mươi trang. Thật tình cờ may mắn, một Thầy dòng Neapolitan, Paolo Antonio Foscarini, cho xuất bản một quyển sách trong cùng năm bàn luận chi tiết rằng chuyển động của Trái Đất là tương thích với Kinh Thánh. Vào tháng Mười Hai 1615, sau một thời gian trì hoãn do bệnh tật, đích thân Galileo đi tới Rome và ngăn học thuyết Copernicus bị phán là dị giáo.
Trong chừng mực quan tâm của Đức Hồng y Roberto Bellarmine, nhà thần học Công giáo hàng đầu thời kì ấy, vấn đề quan tâm chủ yếu là bản chất giả thuyết của bức tranh Copernicus. Sau đây là lời của ông, viết vào ngày 12 tháng Tư 1615 gửi cho Foscarini, sau khi Thư gửi Christina được lưu truyền ở Rome.
… tôi thấy hình như Đức Cha (Foscarini) và Ngài Galileo hành động thận trọng bằng cách hạn chế mình chỉ nói giả định12 chứ không tuyệt đối, như tôi tin rằng Copernicus từng nói. Vì chẳng có gì nguy hiểm khi nói thế, bằng cách giả định Trái Đất chuyển động và Mặt Trời đứng yên, người ta làm cho mọi thứ sáng sủa hơn so với việc giả định các nội luân và ngoại luân; và như thế là đủ cho nhà toán học rồi.
Tuy nhiên, nó khác với việc muốn khẳng định rằng trên thực tế Mặt Trời ngự tại trung tâm của thế giới và nó chỉ quay xung quanh nó chứ không chuyển động từ đông sang tây, và rằng Trái Đất nằm trong tầng trời thứ ba và quay với tốc độ lớn xung quanh Mặt Trời; đây là một điều rất nguy hiểm, có khả năng không chỉ ghẹo gan mọi nhà triết học kinh viện và nhà thần học, mà còn gây hại cho Đức tin Tôn giáo bởi việc nói rằng Kinh Thánh đã sai.13
Ẩn sau những nhận xét này là một sự phê bình vô cùng mạnh mẽ đối với sự ủng hộ của Galileo với bức tranh Copernicus. Thật không đúng nếu suy luận, như Galileo đã làm, rằng việc quan sát thấy các pha của Kim tinh chứng tỏ rằng bức tranh Copernicus là đúng. Ví dụ, trong vũ trụ học Tycho, trong đó các hành tinh quay xung quanh Mặt Trời, còn Mặt Trời và các hành tinh quay xung quanh Trái Đất (Hình 2.7), các pha của Kim tinh sẽ được quan sát thấy y hệt như trong bức tranh Copernicus. Theo Gingerich, đây là lỗi logic trọng yếu của Galileo. Nói cho chặt chẽ, ông chỉ có thể đưa ra một nhận định giả thuyết mà thôi.
Những phát hiện của Tòa án Dị giáo rất có lợi cho cá nhân Galileo – ông được tha bổng cho tội danh nghi ngờ dị giáo. Tuy nhiên, Tòa án Dị giáo cũng yêu cầu một ủy ban gồm mười một chuyên gia cho ý kiến về hiện trạng của học thuyết Copernicus. Vào ngày 16 tháng Hai 1616, ủy ban báo cáo nhất trí rằng học thuyết Copernicus là tha hóa về mặt triết học và khoa học và dị giáo xét theo thần học. Phán xét này là nguyên nhân chính đưa đến việc kết án Galileo sau này. Có vẻ như Tòa án Dị giáo đã hiểu nhầm kết cục này vì họ chẳng đưa ra lời lên án chính thức nào. Thay vào đó, họ ban hành hai hướng dẫn nhẹ nhàng hơn. Thứ nhất, Galileo được Đức Hồng y Bellarmine cảnh báo riêng rằng ông nên ngừng bảo vệ cho bức tranh thế giới kiểu Copernicus. Chính xác hai bên đã nói những gì là nội dung gây tranh cãi, song Bellarmine báo cáo về Tòa án Dị giáo rằng lời cảnh báo đã được đưa ra và Galileo đã chấp thuận.
Kết quả thứ hai là một sắc lệnh công của Hội đồng Sách cấm. Thứ nhất, nó khẳng định rằng học thuyết về chuyển động của Trái Đất là dị giáo; thứ hai, sách của Foscarini bị lên án và cho vào Danh mục cấm; thứ ba, cuốn De Revolutionibus của Copernicus bị đình chỉ cho đến khi một số đoạn vi phạm được sửa đổi; thứ tư, toàn bộ những quyển sách tương tự đều cho vào danh mục cấm.
Tin đồn lưu truyền nói rằng Galileo đã bị xét xử và bị lên án bởi Tòa án Dị giáo, và để khắc phục, Bellarmine đã nêu một tuyên bố ngắn gọn về kết quả Galileo không bị xét xử cũng không bị lên án, mà ông được thông báo về Sắc lệnh Sách cấm và yêu cầu không được tán thành hay bảo vệ bức tranh Copernicus. Mặc dù cá nhân được miễn xá, nhưng kết quả đó là một thất bại rõ ràng đối với Galileo. Mặc dù không chính thức là dị giáo, nhưng việc tán thành các quan điểm Copernicus thì cũng coi như vậy.
3.5 Vụ xét xử Galileo
Trong bảy năm tiếp theo đó, Galileo giữ thân giữ phận và tuân thủ các quy định của giáo hội. Năm 1623, Gregory XV qua đời và người kế vị của ông, Đức Hồng y Maffeo Barbarini, được bầu làm Giáo hoàng Urban VIII. Ông là người Florence và có cái nhìn thoải mái hơn so với người tiền nhiệm trong việc lí giải kinh sách. Là một người cảm phục Galileo, ông tán thành việc học thuyết Copernicus có thể được thảo luận trên lí thuyết và nó cũng tỏ ra có giá trị lớn trong việc đưa ra các dự báo thiên văn. Galileo có sáu buổi trò chuyện với Urban VIII vào mùa xuân 1624 và đi tới kết luận rằng học thuyết Copernicus có thể được thảo luận, miễn là nó chỉ được xét trên lí thuyết.
Galileo trở về Florence và lập tức bắt tay vào viết quyển Đối thoại về Hai Hệ thống Thế giới Chính: Ptolemy và Copernicus. Ông tin rằng mình đã rất cố gắng để tuân thủ các mong muốn của cơ quan kiểm duyệt. Lời nói đầu được viết chung bởi Galileo và người kiểm duyệt, và sau một số trì hoãn, chuyên luận đồ sộ này được xuất bản vào năm 1632. Galileo viết quyển sách ở hình thức đối thoại giữa ba nhân vật, Simplicio bảo vệ vị thế Aristotle và Ptolemy, Salviati bảo vệ vị thế Copernicus và Sagredo là người quan sát trung lập và là một người con của thế giới. Trước sau như một, Galileo lập luận rằng mục đích không phải là để đưa ra phán xét, mà để truyền đạt thông tin và khai sáng. Quyển sách được xuất bản với đầy đủ giấy phép của giáo hội.
Hai Hệ thống Thế giới Chính được giới khoa học đón nhận, nhưng chẳng mấy chốc những lời phàn nàn và tin đồn bắt đầu lan truyền ở Rome. Một tài liệu đề tháng Hai 1616, gần như chắc chắn là ngụy tạo, được tìm thấy trong đó Galileo đặc biệt bị cấm thảo luận về học thuyết Copernicus ở mọi hình thức. Đến lúc này, Đức Hồng y Bellarmine đã qua đời 11 năm. Trên thực tế, Galileo không còn xem mô hình Copernicus trên giả thuyết nữa, mà là một sự thật về tự nhiên – Salviati là Galileo nói lên suy nghĩ của chính mình. Hệ thống Copernicus được khắc họa thuận lợi hơn nhiều so với bức tranh Ptolemy, đi ngược lại với các điều kiện của Urban VIII cho phép thảo luận về hai hệ thống thế giới.
Đức Giáo hoàng buộc phải hành động – uy quyền của giáo hoàng đang bị suy sụp khi mà sự chống lại cải cách và tái khẳng định quyền uy đó là những xem xét chính trị tối quan trọng. Galileo, lúc này đã 68 tuổi và sức khỏe kém, được lệnh đến Rome với nguy cơ bị bắt giữ. Kết quả xét xử là một kết luận đã được định trước. Cuối cùng, Galileo nhận một tội danh nhẹ hơn trên cơ sở rằng, giả như ông vi phạm các điều kiện áp đặt lên ông vào năm 1616, thì ông đã không cố ý làm thế. Giáo hoàng khăng khăng đòi thẩm vấn dưới sự đe dọa tra khảo. Vào ngày 22 tháng Sáu 1633, Galileo bị kết tội ‘nghi ngờ dị giáo mức nặng’ và buộc phải công khai từ bỏ quan điểm, các thủ tục được ghi lại trong Sách Sắc lệnh.
Tôi không giữ quan điểm này của Copernicus, và tôi đã không giữ nó sau khi được lệnh phải từ bỏ nó. Thế thôi, nay tôi có mặt ở đây trong tay các ngài; tùy các ngài xử trí.14
Cuối cùng Galileo trở về Florence và chịu quản thúc tại nhà cho đến cuối đời – ông qua đời tại Arcetri vào ngày 9 tháng Một 1642.
Với tinh thần bất khuất, Galileo tiếp tục viết công trình vĩ đại nhất của ông, Đàm luận và Chứng minh Toán học về Hai Khoa học Mới Liên quan đến Cơ học và Chuyển động Cục bộ, thường được gọi đơn giản là Hai Khoa học Mới, xuất bản vào năm 1638. Trong chuyên luận này, ông tập hợp lại những hiểu biết về thế giới vật lí mà ông đã thu nhặt được trong cả đời mình. Những nhận thức căn bản về nền khoa học mới thứ hai – đó là phân tích chuyển động.
3.6 Nguyên lí tương đối Galileo
Những ý tưởng trình bày trong Hai Khoa học Mới đã có trong đầu Galileo từ năm 1608. Một trong số đó là cái ngày nay được gọi là nguyên lí tương đối Galileo. Sự tương đối thường được xem là thứ gì đó được phát minh bởi Albert Einstein vào năm 1905, nhưng như thế là không công bằng với thành tựu vĩ đại của Galileo. Giả sử một thí nghiệm được tiến hành trên bờ biển và rồi một con tàu chuyển động ở tốc độ không đổi so với bờ biển. Nếu bỏ qua sức cản không khí thì có khác biệt nào không ở kết cục của các thí nghiệm? Galileo trả lời như đinh đóng cột, ‘Không, không hề có.’
Sự tương đối của chuyển động được minh họa bằng cách thả rơi một vật từ đỉnh cột buồm của một con tàu (Hình 3.8). Nếu con tàu đứng yên, thì vật rơi thẳng đứng xuống. Bây giờ giả sử con tàu đang chuyển động. Giả sử vật được thả rơi từ đỉnh cột buồm, nó phải rơi thẳng đứng xuống theo một người quan sát ở trên tàu. Tuy nhiên, người quan sát đứng yên trên bờ biển để ý thấy rằng, so với bờ biển, quỹ đạo của vật bị cong (Hình 3.8c). Lí do là vì con tàu đang chuyển động ở một tốc độ v nào đó và vì thế, so với bờ biển, vật có hai thành phần tách biệt cho chuyển động của nó – gia tốc thẳng đứng xuống dưới do trọng lực và chuyển động thẳng đều theo phương ngang do chuyển động của con tàu.

Hình 3.8 (a) Thả rơi một vật từ đỉnh cột buồm trên một con tàu đứng yên trong hệ quy chiếu S. (b) Thả rơi một vật từ đỉnh cột buồm trên một con tàu chuyển động, nhìn trong hệ quy chiếu S’ của con tàu. (c) Thả rơi một vật từ đỉnh cột buồm trên một con tàu chuyển động, khi quan sát từ hệ quy chiếu S. Con tàu chuyển động trong thời gian vật rơi.
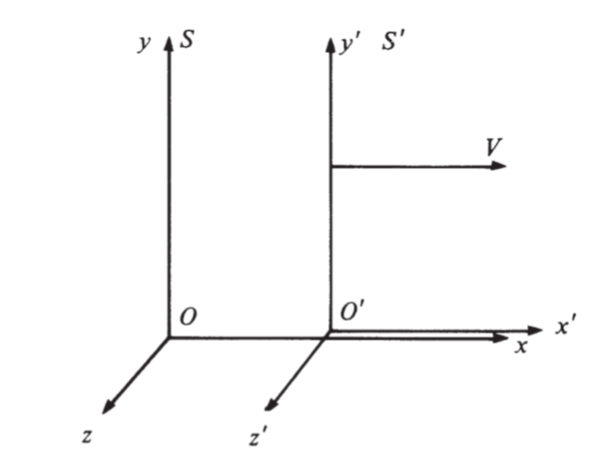
Hình 3.9 Minh họa hai hệ quy chiếu Descartes đang chuyển động ở vận tốc tương đối v theo chiều dương trục x trong ‘cấu hình chuẩn’.
Điều này tự nhiên dẫn tới khái niệm hệ quy chiếu. Khi đo vị trí của một vật nào đó trong không gian ba chiều, ta định vị nó bởi các tọa độ của nó trong một hệ tọa độ hình chữ nhật nào đó (Hình 3.9). Điểm P có tọa độ (x, y, z) trong hệ quy chiếu S đứng yên này. Bây giờ giả sử con tàu chuyển động theo chiều dương trục x ở một tốc độ v nào đó. Khi ấy, ta có thể thiết lập một hệ quy chiếu khác, S’ trên con tàu. Tọa độ của điểm P trong S’ là
(x’, y’, z’). Bây giờ ta dễ dàng liên hệ các tọa độ trong hai hệ quy chiếu này. Giả sử vật đứng yên trong hệ quy chiếu S, x là một hằng số còn giá trị của x’ thay đổi vì x’ = x – vt, trong đó t là thời gian, giả sử gốc tọa độ của hai hệ quy chiếu trùng nhau tại t = 0. Giá trị của y và y’ vẫn bằng nhau trong S và S’, z và z’ cũng thế. Ngoài ra, thời gian là như nhau trong hai hệ quy chiếu. Ta có thể suy ra một tập hợp liên hệ các tọa độ của vật trong S và S’:

Tập hợp này được gọi là phép biến đổi Galileo giữa hệ quy chiếu S và S’. Các hệ quy chiếu chuyển động ở tốc độ không đổi với nhau được gọi là hệ quy chiếu quán tính. Ta có thể tóm tắt nhận thức vĩ đại của Galileo bằng cách phát biểu rằng các định luật vật lí là như nhau trong mọi hệ quy chiếu quán tính.
Một hệ luận của nhận thức này là định luật về thành phần vận tốc. Tôi đã dùng từ tốc độ thay cho vận tốc vì tôi đang khai thác công dụng hiện đại của tốc độ là một đại lượng vô hướng, còn khi dùng vận tốc ý tôi là đại lượng vector v có cả độ lớn và chiều. Galileo là người đầu tiên thiết lập định luật về thành phần vận tốc – nếu một vật có các thành phần vận tốc theo hai chiều khác nhau, thì có thể xác định chuyển động của vật đó bằng cách cộng các tác dụng riêng của những chuyển động này. Đây là cách ông chứng minh rằng quỹ đạo của đạn pháo và vật bị ném có dạng parabol (Hình 3.5).
Trong quyển Hai Khoa học Mới, Galileo đã mô tả những khám phá của ông về bản chất của gia tốc không đổi, chuyển động của con lắc và sự rơi tự do dưới tác dụng của trọng lực. Cuối cùng, ông phát biểu định luật quán tính khẳng định rằng một vật sẽ chuyển động ở vận tốc không đổi trừ khi có một xung lực hoặc một lực làm nó thay đổi vận tốc đó – lưu ý rằng lúc này vận tốc, chứ không phải tốc độ, là không đổi vì chiều chuyển động không đổi khi không có lực tác dụng. Điều này thường được gọi là sự bảo toàn chuyển động – khi không có lực tác dụng, các thành phần riêng của vận tốc vẫn bất biến. Từ quán tính được dùng ở đây theo nghĩa là nó là một tính chất của vật chống lại sự thay đổi chuyển động. Định luật này sẽ trở thành định luật thứ nhất của Newton về chuyển động. Có thể thấy rõ vì sao chuyển động của Trái Đất không gây trở ngại gì cho Galileo. Do nhận thức của ông về sự tương đối Galileo, ông nhận ra rằng các định luật vật lí là không đổi cho dù Trái Đất đứng yên hay đang chuyển động ở một tốc độ không đổi.
3.7 Nhận xét, kết luận
Chúng ta không thể khép lại nghiên cứu này mà không đánh giá những hàm ý phương pháp luận và triết lí của trường hợp Galileo. Giáo hội đã phạm sai lầm khi kết tội nền vật lí mới của Copernicus và Galileo. Phải 350 năm sau thì Giáo hoàng John Paul II mới thừa nhận đã có sai lầm đó. Vào tháng Mười Một 1979, Giáo hoàng John Paul II nói rằng Galileo ‘…đã phải chịu thiệt thòi lớn – chúng ta không thể che giấu thực tế ấy – trong tay những con người và tổ chức của Giáo hội’. Ông tiếp tục thừa nhận rằng ‘…trong vụ án này, các thỏa thuận giữa tôn giáo và khoa học là nhiều hơn và, trên hết thảy, chúng quan trọng hơn những điều chưa hiểu hết đã dẫn tới sự xung đột cay đắng và đầy đau đớn vẫn tiếp tục diễn ra trong hàng thế kỉ sau đó.’
Đối với các nhà khoa học, vấn đề trọng tâm là bản chất của kiến thức khoa học và quan niệm về chân lí trong các khoa học vật chất. Phần nào luận cứ của Đức Hồng y Bellarmine là đúng. Cái Copernicus thu được là một mô hình đẹp hơn nhiều và tiện lợi hơn nhiều so với bức tranh Ptolemy để tìm hiểu chuyển động của Mặt Trời, Mặt Trăng, và các hành tinh, nhưng hiểu theo nghĩa nào đó nó có phải là chân lí hay không? Nếu người ta có đủ cố gắng, thì ngày nay một mô hình kiểu Ptolemy về Hệ Mặt Trời có thể được tạo ra, nó sẽ tái hiện chính xác chuyển động của các hành tinh trên bầu trời, nhưng nó sẽ vô cùng phức tạp và chẳng đem lại mấy kiến thức về vật lí nền tảng. Giá trị của mô hình mới không chỉ ở chỗ nó đem lại một khuôn khổ nhất quán và đơn giản hơn nhiều để hiểu được chuyển động quan sát thấy của các thiên thể, mà còn ở chỗ, trong tay của Isaac Newton, nó đã trở thành một lộ trình để thu được sự hiểu biết sâu sắc hơn rất nhiều về các định luật của chuyển động nói chung, dẫn tới sự thống nhất của vật lí thiên thể, các định luật về chuyển động và định luật hấp dẫn. Một mô hình thỏa mãn có khả năng không những giải thích nhanh gọn số lượng lớn hiện tượng quan sát và thực nghiệm đủ loại, mà còn có thể mở rộng để đưa ra những tiên đoán định lượng về những hiện tượng rõ ràng chẳng có liên quan gì.
Lưu ý rằng tôi dùng từ mô hình trong mô tả tiến trình này chứ không ấn định rằng nó là chân lí. Thành tựu to lớn của Galileo là đã nhận ra rằng các mô hình mô tả tự nhiên có thể được xây dựng trên một nền tảng toán học chắc chắn. Trong phần nhận xét có lẽ nổi tiếng nhất của ông, ông trình bày trong chuyên luận Il Saggiatore (Người làm Thí nghiệm) năm 1624 rằng:
Triết học được trình bày trong quyển sách rất hay này luôn nằm trước mắt chúng ta (ý tôi là Vũ trụ), nhưng người ta không thể hiểu nó trừ khi trước tiên người ta học cách hiểu ngôn ngữ và nhận ra các kí tự trình bày nó. Nó được viết bằng ngôn ngữ toán học, và kí tự là các tam giác, đường tròn, và các dạng hình học khác; không có những phương tiện này con người không thể hiểu được một từ nào của nó; không có những phương tiện này người ta chỉ có thể mò mẩm trong một mê cung tăm tối.15
Nhận xét này thường được rút gọn thành câu phát biểu:
Sách về Tự nhiên được viết bằng các kí tự toán học.
Đây là thành tựu to lớn của cuộc cách mạng Galileo. Những sự thật cơ bản thấy rõ do Galileo thiết lập đòi hỏi một mức trừu tượng rất lớn. Vật chất không tuân theo các định luật đơn giản biểu kiến của Galileo – luôn luôn có ma sát, các thí nghiệm chỉ có thể được tiến hành với độ chuẩn xác hạn chế và thường cho kết quả âm tính. Cần có một nhận thức sâu sắc và trí tưởng tượng để dọn sạch rác rến không cần thiết và đánh giá đúng tính đơn giản cơ bản của cách hành xử của vật chất. Phương pháp hiện đại tiếp cận khoa học chẳng gì hơn là sự hình thức hóa của tiến trình mà Galileo đã khởi xướng. Nó được gọi là phương pháp diễn dịch giả thuyết theo đó các giả thuyết được nêu ra và các hệ quả được suy luận logic từ chúng. Mô hình này có thể chấp nhận được miễn là nó không đi tới xung đột với cách vật chất hành xử trên thực tế. Thế nhưng các mô hình chỉ có giá trị trong phạm vi đã vạch rõ của không gian tham số. Các chuyên gia trở nên gắn bó với chúng, và như những nhận xét của Dirac và Douglas Gough trích dẫn ở Chương 1 mô tả sự cần thiết phải hài lòng với những lí thuyết gần đúng và nỗi đau thật sự phải chịu khi buộc phải từ bỏ một định kiến đã ấp ủ bấy lâu.
Ngày nay, hiếm khi các giáo điều tôn giáo gây trở ngại cho sự phát triển của các khoa học vật chất. Tuy nhiên, thành kiến khoa học và giáo lí là cái chung của tranh luận khoa học. Chẳng có gì đáng lo ngại về điều này miễn là chúng ta nhận ra những gì đang xảy ra. Các định kiến đem lại khuôn khổ để thực hiện tranh luận và để đề xuất các thí nghiệm và tính toán có thể đem lại phép thử về tính nhất quán của các ý tưởng. Ta sẽ tìm thấy nhiều ví dụ trong suốt quyển sách này trong đó ‘chính quyền’ và ‘người có danh vọng’ là rào cản đối với sự tiến bộ khoa học. Cần rất nhiều sự quả cảm và kiên trì để chống lại sức nặng quá lớn của quan điểm bảo thủ. Thông qua sự bảo trợ của khoa học, giáo điều khoa học có thể thu được uy quyền để loại trừ những phương pháp khác. Một trong những ví dụ bất hạnh nhất là vụ án Lysenko ở Liên Xô không bao lâu sau Thế chiến Thứ hai, khi nền triết học chính trị Cộng sản có tác động mạnh lên khoa sinh vật học, đưa đến thảm họa cho những nghiên cứu này ở Liên Xô.
Tôi muốn giới thiệu hai ví dụ thời sự mà tôi sẽ theo đuổi chi tiết hơn ở Chương 21. Thật thú vị khi mà ý tưởng về sự lạm phát trong những giai đoạn đầu dãn nở của Vũ trụ gần như đã có được vị thế ‘giáo điều được công nhận’ trong phần lớn cộng đồng vũ trụ học. Có những lí do hay ho để giải thích vì sao ý tưởng này nên được xem xét nghiêm túc nhưng không có bằng chứng thực nghiệm trực tiếp nào cho cơ sở vật lí đã gây ra sự dãn nở lạm phát trong Vũ trụ sơ khởi. Thật vậy, thủ tục chung là làm ngược lại và ‘rút ra’ cơ sở vật lí của sự lạm phát từ yêu cầu giải thích các đặc điểm của Vũ trụ mà chúng ta quan sát thấy ngày nay. Khi đó, các lí thuyết vật lí hạt có thể được viện dẫn để giải thích những yêu cầu này. Có một sự nguy hiểm rõ ràng khi đi tới nhất quán mà không hề có phép kiểm tra thực nghiệm độc lập nào của lí thuyết. Có lẽ đó là điều tốt nhất chúng ta có thể hi vọng, thế nhưng một số người trong chúng ta sẽ vẫn giữ thái độ hoài nghi cho đến khi có những luận cứ độc lập hơn ủng hộ những giả thuyết này.
Phương pháp luận giống như vậy đã xảy ra trong lí thuyết hạt sơ cấp với sự phát triển lí thuyết dây. Sự ra đời của các lí thuyết trường lượng tử nhất quán liên quan đến các đối tượng một chiều thay cho các hạt điểm có một thành tựu khá đáng chú ý. Phiên bản mới nhất của những lí thuyết này dùng sự lượng tử hóa lực hấp dẫn như một thành phần thiết yếu. Thế nhưng, những lí thuyết này vẫn chưa thể đem lại những dự đoán có thể kiểm tra bằng thực nghiệm. Tuy nhiên, đây là lĩnh vực trong đó nhiều nhà vật lí danh giá nhất đã tập trung công sức của họ. Người ta tin rằng đây là cách hứa hẹn nhất để giải quyết những vấn đề này, bất chấp thực tế rằng có thể sẽ rất khó, nếu không nói là không thể, kiểm tra lí thuyết ấy bằng bất cứ thí nghiệm hay quan sát nào trong tương lai trước mắt.
Ghi chú
1. Lịch sử gần đây về vụ án Galileo được trình bày trong Giáo hội và Galileo, E. McMullin biên tập (2006). Notre Dame, Indiana: NXB Đại học Notre Dame. Chương 13 ‘Nỗ lực Mới nhất của Giáo hội nhằm Xua tan Huyền thoại Galileo’ của George V. Coyne, S. J. là một chuyên luận đặc biệt sáng tỏ.
2. Drake, S (1990). Galileo: Nhà Khoa học Tiên phong, trang 63. Toronto: NXB Đại học Toronto.
3. Lưu ý rằng nếu quả cầu lăn xuống mặt phẳng nghiêng mà không trượt, gia tốc sẽ chỉ là5 gsinq, vì quả cầu có động năng thẳng lẫn động năng quay khi thế năng trọng trường7 giảm.
4. Drake, S. (1990), sách đã dẫn, trang 83.
5. Drake, S. (1990), sách đã dẫn, trang 84.
6. Galilei, G. (1610). Sidereus Nuncius, Venice. Xem bản dịch của A. van Helden (1989). Sidereus Nuncius hay Người đưa tin Thiên văn. Chicago: NXB Đại học Chicago. Thật đáng kinh ngạc, các quan sát và phác thảo được gửi đến xuất bản ngay trước khi mực in kịp khô. Những quan sát cuối cùng được thực hiện vào ngày 2 tháng Ba 1610 và quyển sách được xuất bản vào ngày 13 tháng Ba cùng năm.
7. Finocchiaro, M.A. (1989). Vụ án Galileo: Một Tư liệu Lịch sử. Berkeley: NXB Đại học California.
8. Finocchiaro, M. A. (1989), sách đã dẫn, trang 24.
9. Finocchiaro, M. A. (1989), sách đã dẫn, trang 24.
10. Gingerich, O. (1982), Scientific American, 247, 118.
11. Finocchiaro, M. A. (1989), sách đã dẫn, trang 28.
12. Từ này thường được dịch trên giả thuyết.
13. Finocchiaro, M. A. (1989), sách đã dẫn, trang 67.
14. Finocchiaro, M. A. (1989), sách đã dẫn, trang 287.
15. Sharratt, M. (1994). Galileo: Nhà phát minh Kiên định, trang 140. Cambridge: NXB Đại học Cambridge.
Trích từ Theoretical Concepts in Physics, bản in lần thứ ba 2020,
của Malcolm Longair. Bản dịch của Trần Nghiêm.