Hà Lan, 1621. Góc khúc xạ của ánh sáng truyền giữa hai môi trường phụ thuộc vào chiết suất của hai môi trường đó và được mô tả định lượng bằng định luật Snell.
Tham khảo chéo: Johannes Kepler và Các phương trình Maxwell
Vào năm Snell khám phá ra định luật khúc xạ, người Anh đang cố gắng thuộc địa hóa vùng Nova Scotia và Newfoundland, và khoai tây được trồng lần đầu tiên ở nước Đức. Con tàu Mayflower căng buồm từ thuộc địa Plymouth ở Bắc Mĩ trên hành trình trở về nước Anh.
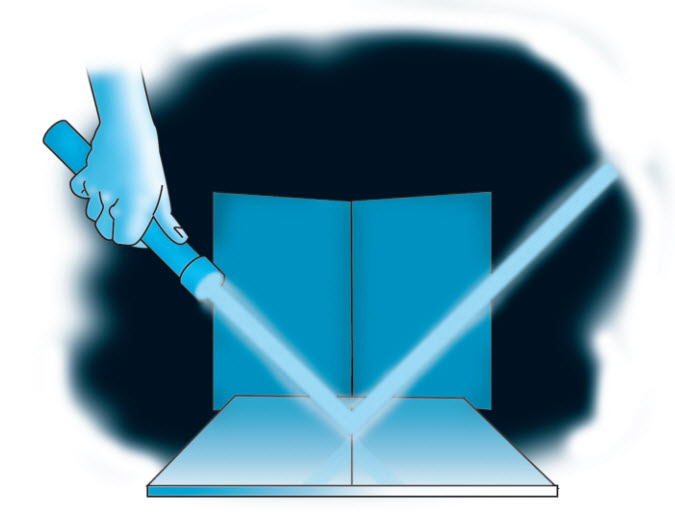
Ánh sáng truyền trong không khí gãy khúc, hay khúc xạ, khi nó đi vào một môi trường khác ví dụ như thủy tinh. Khi các sóng như sóng ánh sáng bị khúc xạ, chúng chịu sự biến đổi hướng truyền do sự biến đổi ở vận tốc của chúng. Sự khúc xạ thường xảy ra khi một tia sáng đi từ một môi trường sang môi trường khác, và mỗi chất liệu đã biết đều làm chậm ánh sáng so với tốc độ của nó trong chân không. Đặc biệt, sự khúc xạ ánh sáng xảy ra tại ranh giới giữa hai môi trường (ví dụ, giữa không khí và nước), tại điểm mà vận tốc pha của ánh sáng biến đổi, và ánh sáng đổi hướng truyền. Ngoài ra, bước sóng của ánh sáng thay đổi tại mặt phân cách giữa hai môi trường, nhưng tần số ánh sáng vẫn không đổi.
Để hiểu khái niệm vận tốc pha, hãy tưởng tượng một gợn hình sin làm bằng gỗ và đang trượt sang phải. Vận tốc pha đơn giản là tốc độ bình thường mà gợn bằng gỗ đang chuyển động. Bây giờ hãy tưởng tượng một sóng trong hồ nước, trong đó một chiếc lá trên mặt hồ đang dao động thẳng đứng khi sóng truyền qua. Trong trường hợp này, hình ảnh sóng chuyển động sang phải với vận tốc pha vp, giống hệt như gợn gỗ, còn chiếc lá có thể chẳng có chuyển động ngang nào hết.
Tôi thích chứng minh sự khúc xạ với mấy bạn trẻ bằng cách nhúng ngón tay của tôi vào hồ nuôi cá cảnh loại lớn. Do không khí có chiết suất 1,0003 và nước có chiết suất 1,33 cho nên khi các vị khách nhìn vào ngón tay chỉ thẳng của tôi nhúng một phần trong nước, ngón tay có vẻ bị gãy đột ngột tại mặt nước. Trước khi bọn cá tới cắn ngón tay tôi, tôi giải thích với các vị khách trẻ rằng sự bẻ cong biểu kiến này là do sự bẻ cong của các tia sáng khi chúng đi từ nước ra không khí. Sau đó, tôi viết nguệch ngoạc định luật Snell lên cái khăn ăn,
n1sin(q1) = n2sin(q2)
và giải thích cách sử dụng định luật để tính mức độ ánh sáng bị khúc xạ khi truyền từ không khí vào nước. (Bạn có thể chứng minh hiện tượng này một cách an toàn hơn với một cái bút chì và một cốc nước.) Ở đây, n1 và n2 là chiết suất của môi trường 1 và 2. Góc giữa ánh sáng tới và một đường vuông góc với mặt phân cách được gọi là góc tới, q1. Tia sáng tiếp tục đi từ môi trường 1 vào môi trường 2 và rời mặt phân cách giữa hai môi trường với góc q2 hợp với đường vuông góc với mặt phân cách. Góc thứ hai này được gọi là góc khúc xạ.
Hãy nhớ rằng sự khúc xạ ám chỉ sự gãy khúc của một sóng khi nó đi vào một môi trường trong đó tốc độ của nó thay đổi. Khi ánh sáng đi từ một “môi trường nhanh” sang một “môi trường chậm”, sự khúc xạ làm gãy tia sáng về phía pháp tuyến (đường thẳng tưởng tượng vuông góc) với mặt phân cách giữa hai môi trường. Lượng gãy khúc phụ thuộc vào n1 và n2 và được mô tả định lượng bằng định luật Snell.
Chiết suất n của nước, thủy tinh, không khí, hay bất kì vật liệu nào là hệ số mà vận tốc pha của sóng điện từ bị chậm đi trong vật liệu đó, so với vận tốc của nó trong chân không, n phụ thuộc vào bước sóng của bức xạ đang nghiên cứu. Một số giá trị thí dụ cho n ở bước sóng 589,3 nm là chân không 1; không khí 1,00029; nước lỏng 1,333; thủy tinh 1,5 – 1,9; và kim cương 2,419.
Định luật phản xạ ánh sáng, ở dạng đơn giản phát biểu rằng góc phản xạ của một tia sáng khỏi một bề mặt bằng với góc tới, cùng định luật khúc xạ ánh sáng có thể được suy ra từ các phương trình điện học và từ học của James Clerk Maxwell và thường áp dụng đúng cho một vùng rộng của phổ điện từ. Hai định luật trên cũng có thể được suy luận ra từ các lí thuyết đơn giản hơn của ánh sáng, như lí thuyết đã được trình bày bởi nhà vật lí Hà Lan Christiaan Huygens (1629-1695) vào năm 1678. Huygens sử dụng các hình vẽ để biểu diễn một đầu sóng cho trước sẽ ở đâu tại một thời điểm bất kì.
Sự khúc xạ có vô số ứng dụng ngày nay. Ví dụ, một thấu kính lồi sử dụng sự khúc xạ làm cho các tia sáng song song hội tụ lại. Không có sự khúc xạ ánh sáng bởi thủy tinh thể trong mắt, chúng ta sẽ không thể nhìn đúng và các thấu kính truyền thống dùng cho camera sẽ không tồn tại. Ví dụ, sóng địa chấn – các sóng năng lượng gây ra bởi sự nứt vỡ đột ngột của đá dưới lòng đất –thay đổi tốc độ bên trong Trái Đất và bị gãy khúc khi chúng đi tới mặt ranh giới giữa các vật liệu theo định luật Snell. Các nhà địa chất có thể nghiên cứu các lớp bên trong Trái Đất bằng cách nghiên cứu hành trạng của các sóng khúc xạ và phản xạ.
Khi một chùm ánh sáng truyền từ một vật liệu chiết suất cao sang một vật liệu chiết suất thấp, dưới những điều kiện nhất định, chùm tia có thể bị phản xạ toàn bộ. Hiện tượng quang học này thường được gọi là phản xạ toàn phần, và nó xảy ra khi ánh sáng bị khúc xạ tại mặt phân cách môi trường đến mức nó bị phản xạ ngược lại. Đó là trường hợp trong các loại sợi quang nhất định, trong đó ánh sáng đi vào một đầu bị giữ lại bên trong cho đến khi nó ló ra ở đầu bên kia.
Bạn có thể sử dụng định luật Snell để tìm hiểu và tính toán điều kiện cần thiết cho sự phản xạ toàn phần. Trước tiên, cho góc khúc xạ q2 = 90o, rồi tính góc tới. Vì ta không thể làm khúc xạ ánh sáng nhiều hơn 90o, nên dưới điều kiện này, toàn bộ ánh sáng sẽ phản xạ đối với các góc tới lớn hơn góc cho bởi góc khúc xạ 90o.
Đặc điểm của kim cương gia công đem lại một ví dụ nữa cho sự phản xạ toàn phần. Các chùm ánh sáng bị phản xạ bên trong tinh thể kim cương có hình dạng chính xác nên kim cương lóng lánh và thường phát ra ánh sáng theo hướng của mắt người nhìn. Nói cách khác, việc cắt kim cương khai thác sử dụng sự phản xạ toàn phần để phần lớn ánh sáng lọt vào kim cương bị phản xạ bên trong kim cương cho đến khi chúng ló ra ở những mặt trên nhất định làm cho kim cương sáng lấp lánh. Mỗi tia sáng thường chịu vài lần phản xạ toàn phần trước khi ló ra khỏi kim cương.
Sự phản xạ toàn phần giúp giam cầm ánh sáng để nó truyền dọc theo sợi quang làm bằng vật liệu thích hợp, và nhờ đó sợi quang có thể dẫn sáng đi vòng qua các góc cạnh. Ví dụ, sợi quang có thể tương tự “sợi tóc” thủy tinh mỏng đến mức một khi ánh sáng đi vào ở một đầu, nó không bao giờ có thể chạm tới thành bên trong ở góc nhỏ hơn góc tới hạn gây ra phản xạ toàn phần. Ánh sáng chịu sự phản xạ toàn phần mỗi khi nó đi tới bề mặt sợi quang và cuối cùng đi ra ở đầu kia của sợi quang. Cáp quang được dùng để truyền tín hiệu điện thoại và vi tính và có thể có nhiều ưu điểm so với cáp điện truyền thống. Chẳng hạn, sợi quang có thể mang nhiều thông tin hơn trong một sợi nhỏ hơn truyền nhanh hơn cáp điện, và sợi quang không nhạy với trường điện từ tản lạc xung quanh sợi dẫn. Sợi quang được sản xuất tăng đột biến trong ngành truyền thông thế giới trong hai mươi năm qua và đã cho phép Internet bùng nổ.
Sợi quang cũng được sử dụng trong y khoa, là một cách cho phép các bác sĩ nhìn vào bên trong cơ thể mà ít xâm hại nhất. Một số đèn nội soi sử dụng hai tuyến sợi quang. Một “sợi ảnh” được bao quanh bởi các “sợi sáng” mang ánh sáng đến đầu cuối để soi sáng mô đang quan tâm. Nói cách khác, hai bó sợi tách biệt tồn tại trong đèn nội soi linh hoạt, một để quan sát và một để truyền sáng.
Sự phản xạ toàn phần còn có vai trò trong ảo tượng, ví dụ những ảo tượng có thể xuất hiện trên đường nhựa hoặc trên sa mạc vào ngày nắng nóng. Đặc biệt, thỉnh thoảng người quan sát có thể nhìn thấy ảnh lộn ngược của một quang cảnh và cây cối gần đó như thể chúng bị phản xạ trên hồ nước. Không khí gần mặt đất nóng hơn không khí trên cao và có chiết suất nhỏ hơn chiết suất của không khí lạnh. Ánh sáng từ bất kì điểm nào trên vật truyền xuống có thể bị khúc xạ ra xa pháp tuyến, và khi nó đi gần mặt đất nó bị phản xạ toàn bộ tại lớp không khí chiết suất thấp hơn. Ánh sáng khúc xạ đi vào mắt người quan sát và có thể đem lại sự xuất hiện của ảnh nằm bên dưới mặt đất.
Cho đến năm 2001, toàn bộ những vật liệu đã biết đều có chiết suất dương. Tuy nhiên, vào năm 2001, các nhà khoa học đến từ Đại học California ở San Diego đã mô tả một vật liệu composite khác lạ có chiết suất âm, về cơ bản là đảo ngược định luật Snell. Vật liệu kì lạ này là hỗn hợp gồm sợi thủy tinh, các vòng đồng, và các dây dẫn có khả năng làm hội tụ ánh sáng theo một kiểu mới lạ. Những kiểm tra sơ bộ cho thấy, chẳng hạn, vi sóng ló ra khỏi vật liệu theo đúng hướng ngược lại với định luật Snell dự đoán. Các nhà vật lí Sheldon Schultz, David R. Smith, và Richard A. Shelby nêu giả thuyết rằng vật liệu mới không hẳn chỉ là sự hiếu kì vật lí bởi vì có thể ngày nào đó nó sẽ dẫn đến sự phát triển của các anten mới lạ và các dụng cụ điện từ khác. Trên lí thuyết, một tấm vật liệu chiết suất âm có thể tác dụng như một siêu thấu kính tạo ra các hình ảnh hết sức chi tiết.
Mặc dù đa số các thí nghiệm buổi đầu với những loại vật liệu kì lạ này được tiến hành với vi sóng, nhưng vào năm 2007 một đội nghiên cứu đứng đầu bởi Henri Lezec thuộc Viện Công nghệ California ở Pasadena đã thu được chiết suất âm cho ánh sáng nhìn thấy. Để tạo ra ảnh như thể nó được làm bởi vật liệu khúc xạ âm, đội Lezec đã chế tạo một lăng kính kim loại chia lớp được đục lỗ bởi một mê cung rãnh nhỏ cỡ nano.
Đây là lần đầu tiên các nhà vật lí nghĩ ra một cách làm cho ánh sáng nhìn thấy đi theo hướng ngược lại với cách nó thường gãy khúc khi truyền từ vật liệu này sang vật liệu khác. Một số nhà vật lí đề xuất rằng hiện tượng này một ngày nào đó có thể đưa đến các kính hiển vi quang học để tạo ảnh của các vật nhỏ cỡ phân tử và để chế tạo các dụng cụ tàng hình che giấu các vật thành vô hình.
Năm 2005, Akhlesh Lakhtakia thuộc trường Đại học Pennsylvania và Tom Mackay thuộc Đại học Edinburgh xác định được rằng sự khúc xạ âm xung quanh một lỗ đen quay tròn có thể làm thay đổi vị trí biểu kiến của các ngôi sao khi nhìn từ phía Trái Đất – ít nhất là trên lí thuyết. Nói cách khác, để gây ra khúc xạ không nhất thiết cần một vật liệu truyền thống như thủy tinh hoặc nước; ví dụ, không gian xung quanh một lỗ đen như vậy có thể có các tính chất khúc xạ và có chiết suất âm làm cho ánh sáng khúc xạ theo hướng ngược lại so với các vật liệu truyền thống.
Năm 2007, các nhà vật lí đã tạo ra được một bề mặt “siêu đen” hầu như không phản xạ. Thông thường, ánh sáng phản xạ từ một bề mặt khi nó đi tới ranh giới giữa hai vật liệu có chiết suất khác nhau. Chiết suất của hai vật liệu càng chênh lệch nhiều thì ánh sáng bị phản xạ càng nhiều. Để ngăn cản những phản xạ như vậy ở vật liệu mới lạ của họ, một đội nghiên cứu tại Viện Bách khoa Rensselaer ở Troy, New York, đã chế tạo một bề mặt nhiều lớp làm bằng các sợi nhỏ cỡ nano. Lớp mặt trên cùng có chiết suất 1,05 gần bằng chiết suất 1,0 của không khí. Lớp khoác phản xạ đặc biệt thấp của các nhà nghiên cứu trên hoạt động đối với các bước sóng giữa tử ngoại gần và hồng ngoại gần.
Willebrord Snell, còn gọi là Snellius, Snell, Snel van Royen, hay Willebrord van Snel van Royen (1580-1626), nhà thiên văn và nhà toán học Hà Lan nổi tiếng với định luật khúc xạ mang tên ông.
KHÊU GỢI HIẾU KÌ. Đóng góp lớn nhất của Snell cho khoa học, định luật khúc xạ ánh sáng, không được công bố mãi đến gần bảy mươi năm sau khi ông qua đời. · Ngư dân có kinh nghiệm dùng thuật ngữ “Cửa sổ Snell” để chỉ góc phía trên mặt nước nằm trong tầm nhìn của cá. Người bắt cá tránh bị cá nhìn thấy bằng cách đứng ngoài cửa sổ này, kích cỡ của nó được chi phối bởi định luật Snell. · Nước mưa gây ra cầu vồng thông qua sự khúc xạ. Do các màu sắc ánh sáng khác nhau có bước sóng khác nhau, nên các màu khúc xạ khác nhau khi truyền qua nước. Cầu vồng thật ra là một vòng tròn có tâm tại một điểm ngược hướng với mặt trời so với người nhìn; tuy nhiên, người nhìn không ngắm được toàn bộ vòng tròn vì cảnh quan che mất.
Định luật Snell có thể được suy ra từ nguyên lí Fermat, nguyên lí phát biểu rằng ánh sáng truyền đi theo lộ trình tốn ít thời gian nhất... Trong một thí dụ tương tự kinh điển do Feynman nêu ra, vùng chiết suất thấp được thay thế bằng bờ biển, vùng chiết suất cao được thay thế bằng biển, và lộ trình nhanh nhất cho nhân viên cứu hộ trên bờ biển bơi tới chỗ một người đuối nước ở trên biển là chạy theo lộ trình tuân theo định luật Snell.
- Định luật Snell, Wikipedia
Vào năm 1621, một nhân vật thật sự thông minh với cái tên thật sự hài hước (Willebrord Snell) đã chỉ ra, thông qua thực nghiệm tỉ mỉ, rằng góc lập giữa pháp tuyến bề mặt với tia sáng tới và tia gãy khúc có liên hệ toán học với nhau.
- Mason McCuskey, Lập trình game các hiệu ứng đặc biệt với DirectX

Willebrord Snell
Willebrord Snell chào đời ở Leiden, Hà Lan. Bố ông là một giáo sư toán học. Mặc dù Snell học luật, nhưng ông bị thu hút bởi toán học và vào năm 1600 thì bắt đầu dạy toán tại Đại học Leiden. Không bao lâu sau, ông gặp gỡ những người đương thời nổi tiếng như Tycho Brahe và Johannes Kepler.
Năm 1602, ông học luật ở Paris, và vài năm sau thì ông cho ra tác phẩm lớn đầu tiên của ông liên quan đến khoa học – bản dịch Latin cuốn Wisconstighe Ghedachtenissen (Hồi kí Toán học, 1605-1608) của Simon Steven (1548-1620). Steven là nhà toán học và kĩ sư người Flemish có các tập hồi kí chứa đựng các chuyên luận của ông về toán học, cơ học, và lí thuyết âm nhạc, kế toán, quang học, thiên văn học, và địa lí. Năm 1608, bản dịch của Snell mang tiêu đề Hypomnemata mathematica (Hồi kí toán học).
Năm 1608, Snell cưới vợ. Hai vợ chồng ông có tổng cộng mười tám mặt con, nhưng chỉ có ba người sống đến tuổi trưởng thành. Năm 1613, Snell kế vị bố ông làm giáo sư toán học tại Đại học Leiden. Năm 1615, ông nghiên cứu một phương pháp mới tìm bán kính Trái Đất, sử dụng phương pháp tam giác đạc. Tác phẩm của ông, Eratosthenes Batavus (Eratosthenes Hà Lan), xuất bản năm 1617, mô tả phương pháp tam giác đạc của ông sử dụng ngựa nhà và hai thị trấn địa phương, và khoảng cách giữa chúng, để thực hiện tính toán. Giá trị ông thu được cho chu vi Trái Đất là 38.500 km, tương đối gần với con số thực tế 40.000 km. Ông tiếp tục cải thiện các tính toán với sự trợ giúp của học trò, nhưng ông sớm qua đời vào năm 1626 thành ra các tính toán bổ sung của ông chưa bao giờ được công bố chính thức.
Năm 1619, ông công bố các bài báo về sao chổi. Hai năm sau, trên tờ Cyclometricus, Snell công bố khám phá một phương pháp mới sử dụng các đa giác tính ra số p. Đặc biệt, ông tính ra p đến ba mươi tư chữ số thập phân bằng cách tưởng tượng một đa giác có 1.073.741.824 cạnh, với phương pháp đã được sử dụng trước đó bởi nhà toán học Đức Ludolph Van Ceulen (1540-1610) nhưng chưa hề công bố. Snell cải tiến dựa trên các phương pháp truyền thống tính gần đúng số p bằng cách sử dụng đa giác, sao cho, chẳng hạn, ông có thể sử dụng đa giác 96 cạnh để có các chữ số của p đúng đến bảy chữ số thập phân, trong khi các phương pháp cổ điển chỉ đem lại p với hai chữ số thập phân. [Dành cho độc giả thích tính toán, Snell đã sử dụng p ~ (2/3)nsin(p/n) + (1/3)ntan(p/n) để tính ra p, trong đó n là số cạnh của một đa giác nội tiếp đường tròn.]
Năm 1624, Snell trở thành một chuyên gia về đạo hàng. Ông nghiên cứu một đường cong toán học gọi là đường tà hình, một đường trên mặt cầu lập một góc không đổi với các kinh tuyến. (Kinh tuyến tương ứng với đường tròn lớn trên bề mặt Trái Đất đi qua địa cực bắc và nam.) Công trình của ông về đường tà hình và đạo hàng được công bố trên báo Tiphys batavus. Đường tà hình có hình dạng xoắn cầu và là quỹ đạo lúc di chuyển khi một kim la bàn được giữ theo một hướng nhất định.
Ngày nay, Snell được biết tới nhiều nhất với nghiên cứu của ông về khúc xạ ánh sáng. Mối quan tâm về khúc xạ đã bắt đầu trước đó hàng thế kỉ. Chẳng hạn, Ptolemy (85-165), nhà thiên văn học và địa lí học Hi Lạp có sức ảnh hưởng nhất của thời đại ông, đã xây dựng các bảng góc khúc xạ và góc tới tương ứng cho các môi trường. Ông ước tính tỉ số của hai góc là không đổi với hai môi trường tạo nên một mặt phân cách hay, nói cách khác, q1/q2 = k12. Johannes Kepler cũng đã tiến hành vô số phép đo góc tới và góc khúc xạ tương ứng cho các mặt phân cách môi trường đa dạng, nhưng ông không thể tìm thấy liên hệ chính xác giữa các góc mà ông đã đo. Năm 1621, Snell khi ấy là giáo sư toán học tại Đại học Leiden, nhận thấy phương trình đơn giản của Ptolemy là không chính xác, và ông sớm tìm thấy quy luật đúng thông qua các thí nghiệm của mình. Không giống công thức của Ptolemy, định luật của Snell sử dụng tỉ số của sin của các góc thay cho các góc. Công trình của Snell được lưu hành nội bộ ở dạng bản thảo và chưa được công bố.
Theo các giáo trình vật lí nổi tiếng, ví dụ như Sự phát triển các khái niệm vật lí của Arnold Aron, định luật trên rõ ràng đã thu hút sự chú ý của René Descartes và Huygens, và Descartes đã công bố mối liên hệ trên ở dạng hiện đại vào năm 1637. Nhiều người tin rằng Descartes đã rút ra định luật trên một cách độc lập, và ở Pháp định luật Snell được gọi là định luật Descartes.
Như đã nói ở phần giới thiệu quyển sách này, định luật Snell được phát triển bởi nhiều nhà nghiên cứu trong hàng thế kỉ. Có lẽ người đầu tiên hiểu được mối liên hệ căn bản biểu diễn bởi định luật Snell là nhà toán học Arab Ibn Sahl vào năm 984. Năm 1602, nhà thiên văn và toán học Anh Thomas Harriot cũng khám phá định luật trên, nhưng ông không công bố công trình của mình. Năm 1621, Snell khám phá ra định luật; các ghi ghép không được công bố của ông về vấn đề trên được phát hiện bởi học giả và nhà sưu tầm bản thảo Hà Lan Isaac Vossius vào khoảng năm 1662, và Huygens trình bày định luật trên trong cuốn Dioptrica của ông, xuất bản năm 1703.
Snell qua đời chỉ vài năm sau khám phá trên mà chưa hề công bố chính thức công trình của ông về định luật khúc xạ. Descartes thật sự là người đầu tiên công bố định luật một cách rõ ràng ở dạng hàm sin trong tác phẩm Luận về phương pháp năm 1637 của ông (tác phẩm ban đầu được xuất bản ở Leiden, ở Pháp cùng với tác phẩm Dioptrique của ông). Descartes đã không xác nhận định luật bằng thực nghiệm. Thật ra Huygens cùng một số người khác buộc tội Descartes ăn cắp, vì thực tế Descartes có đến Leiden trong lúc và sau công trình của Snell, nhưng chẳng có bằng chứng nào hậu thuẫn cho sự buộc tội này.
Một miệng hố trên mặt trăng với đường kính 82 km được đặt tên Snellius theo tên Snell và đã được phê chuẩn vào năm 1935 bởi Tổng Liên đoàn Thiên văn Quốc tế.
ĐỌC THÊM
Arons, Arnold, Development of Concepts of Physics (Reading, Mass.: Addison Wesley, 1965).
Barry, Patrick L., “The New Black: A Nanoscale Coating Reflects Almost No Light,” Science News 171(9): 132, March 3, 2007.
Brooks, Michael, “Illusions of a Starry, Starry Night,” New Scientist, số 2502: 30–33, 04/06/2005; có thông tin về lỗ đen và chiết suất âm.
Hung, Edwin, Beyond Kuhn: Scientific Explanation, Theory Structure, Incommensurability and Physical Necessity (Aldershot, Hampshire, U.K.: Ashgate Publishing, 2005).
Leutwyler, Kristin, “New Material Reverses Snell’s Law,” Scientific American,09/04/2001; xem www.sciam.com/article.cfm?articleID=000A27C4-0C1B-1C5EB882809EC588ED9F.
Lezec, Henri J., Jennifer A. Dionne, và Harry A. Atwater, “Negative Refraction at Visible Frequencies,” Science (express online publication), 12/03/2007; xem www.sciencemag.org/cgi/content/abstract/1139266v1.
Livio, Mario, “Ask the Experts: Why Do Rainbows Form?” Scientific American 295(1): 104, 07/2006.
Livio, Mario, “The Quest for the Superlens,” Scientific American, 295(1): 60–70, 07/2006.
Mackay, Tom, Akhlesh Lakhtakia, và Sandi Setiawan, “Gravitation and Electromagnetic Wave Propagation with Negative Phase Velocity,” New Journal of Physics 7(75): 1–14, 2005; xem www.iop.org/EJ/abstract/1367630/7/1/075/.
Rashed, Roshdi “A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses,” Isis, 81: 464–491, 1990; bàn về khả năng Sahl khám phá định luật Snell.
Struik, Dirk, “Snel,” trong Dictionary of Scientific Biography, Charles Gillispie (New York: Charles Scribner’s Sons, 1970).
GIẢI LAO: KHỞI ĐẦU CÂU CHUYỆN
Dường như Trái Đất đã bị lấy đi và tạo lập lại, không phải bởi những người ngoài hành tinh đến từ một cánh tay khác của Ngân hà... mà bởi những sinh vật đến từ một vũ trụ khác, nơi toàn bộ các định luật của tự nhiên khác hẳn với các định luật trong vũ trụ này. Thực tại của con người, cái hoạt động trên các định luật của Einstein, và thực tại hoàn toàn khác của phi con người đã va chạm nhau, mắc cạn tại vùng giao Einstein này. Trong trường hợp xấu nhất của mọi thế giới mới khả dĩ, giờ thì mọi thứ đều có thể xảy ra.
- Dean Koontz, The Taking
Quan niệm nhân quả không đi vào phương trình của định luật Snell. Không có sự phụ thuộc có điều kiện, không có sự bất đối xứng tạm thời giữa nhân và quả biểu thị trong định luật này. Tia sáng tới không gây ra khúc xạ. Người ta có thể hỏi: “Cái gì làm cho các hành tinh chuyển động theo quỹ đạo elip Kepler?”, “Cái gì làm cho các chùm ánh sáng tuân theo định luật Snell?”... Trong các định luật Kepler và định luật Snell, ta tìm thấy các thí dụ của mối liên hệ tất định, trong vật lí cổ điển, mà không có bất kì thành phần nhân quả nào.
- Friedel Weinert, The Scientist As Philosopher: Philosophical Consequences of Great Scientific Discoveries
Các nhà vật lí phải phát minh ra các từ và cụm từ cho các khái niệm khác xa với kinh nghiệm hàng ngày. Lối ưa chuộng của họ là tránh các từ mới sáng chế thuần túy, và thay vậy họ thích liên tưởng, cho dù yếu ớt, đến một câu chuyện tương tự nào đó. Một lựa chọn khác là đặt tên các khám phá và các phương trình theo tên một người khác. Đây cũng là cách họ đã làm. Nhưng nếu bạn không biết rằng họ đang nói về vật lí, thì bạn có thể rất e ngại về họ.
- Carl Sagan, Contact
Thật ra, chúng ta có thể xem hình học là ngành vật lí cổ xưa nhất. Không có hình học, tôi đã chẳng thể thiết lập thuyết tương đối.
- Albert Einstein, trong bức thư “Hình học và Kinh nghiệm” gửi đến Viện Hàn lâm Khoa học Phổ năm 1921.