102. Phương trình phi đại số xex = 2 được giải như thế nào?
Nó được giải tốt nhất bằng đồ thị.
Phương trình đã cho có thể được biểu diễn ở dạng hai phương trình độc lập
y = ex và y = 2/x.
Hai phương trình này kết hợp lại là tương đương với phương trình đã cho: xex = 2.
Tọa độ x của giao điểm của hai đường cong sẽ cho ra giá trị cần tìm của x.
Để vẽ đường cong y = ex, ta sử dụng các giá trị
khi x = 0 y = 1
x= 1 y = e1 = 2,7
x = 2 y = e2 = 7,3
Để vẽ đường cong y= 2/x, ta sử dụng các giá trị
khi x = 0,5 y = 4
x= 1 y = 2
x = 2 y = 1
x= 3 y = 0,6
x = 4 y = 0,5
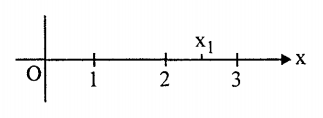
Hai đường cong này được vẽ chung trong một hệ tọa độ như hình bên dưới.
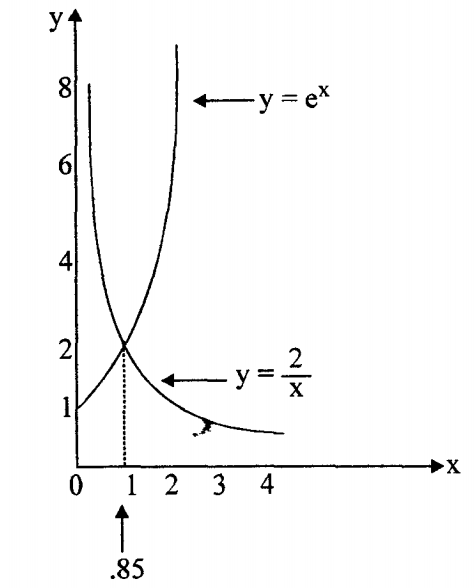
Từ hình vẽ, ta xác định được tọa độ x của giao điểm là 0,85; suy ra nghiệm gần đúng là x = 0,85.
103. Trở lại với đại số trừu tượng! Đại số trừu tượng hiện đại khác như thế nào với đại số cổ điển?
Đại số cổ điển là một khái quát hóa của số học, còn đại số trừu tượng là một nghiên cứu của các cấu trúc đại số.
Các cấu trúc đại số còn được gọi là các hệ thống đại số.
104. Nói cho chính xác thì một hệ thống đại số là gì?
Một hệ thống đại số là một TẬP HỢP những đối tượng gọi là phần tử, cùng với một hoặc nhiều toán tử để kết hợp chúng.
105. Một TẬP HỢP có nghĩa là gì?
Một tập hợp là một nhóm những đối tượng được xác định rõ.
Các phần tử của một tập hợp được ngăn cách nhau bởi dấu phẩy và được viết bên trong cặp ngoặc nhọn.
Ví dụ, tập hợp gồm năm số tự nhiên đầu tiên được viết là A = {1, 2, 3, 4, 5}, trong đó A là tên đặt cho tập hợp.
Các tập hợp thường được kí hiệu bằng các chữ cái viết hoa A, B, C, X,...
Các phần tử thường được kí hiệu bằng các chữ cái viết thường a, b, c,..., x, y, z.
106. Một toán tử có nghĩa là gì?
Một quy tắc kết hợp hai phần tử được gọi là một toán tử.
Phép cộng và phép nhân là ví dụ quen thuộc nhất của toán tử.
107. Cái gì có thể làm các phần tử và toán tử của một tập hợp?
Các phần tử không nhất thiết là những con số, và toán tử không nhất thiết là các phép tính số học.
Khi các toán tử không nhất thiết là phép cộng và phép nhân, chúng được kí hiệu bởi kí tự 0 và *, đọc là không và sao. o là kí tự đầu tiên của ngôn ngữ toán tử.
108. Các hệ thống đại số được sử dụng thường nhất là gì?
Các hệ thống đại số được sử dụng thường nhất là NHÓM, VÀNH, MIỀN NGUYÊN, TRƯỜNG và KHÔNG GIAN VECTOR.
Sự phân loại phụ thuộc vào các tiên đề được thỏa mãn dưới toán tử hoặc những toán tử nhất định đã được định nghĩa cho các phần tử của tập hợp.
109. Tính đóng có nghĩa là gì?
Tính chất nổi bật có chung cho mọi toán tử là toán tử áp dụng cho hai phần tử bất kì của tập hợp tạo ra một phần tử cũng thuộc tập hợp đó. Tính chất này được gọi là tính đóng và hệ được người ta nói là đóng dưới toán tử đó.
Ví dụ, xét tập hợp các số nguyên
I = {...., - 3, - 2, -1, 0, 1, 2, 3,...},
trong đó các dấu chấm chấm có nghĩa là còn chuỗi số nguyên dương và nguyên âm kéo dài đến vô hạn ở cả hai phía.
Tập hợp số nguyên được nói là đóng dưới phép cộng và phép nhân, vì tổng của hai số nguyên bất kì là một số nguyên, và tích của hai số nguyên bất kì cũng là một số nguyên.
Nói theo ngôn ngữ kí hiệu, nếu a và b là hai phần tử của một tập hợp, thì để thỏa mãn tính đóng, phần tử a o b cũng phải là một phần tử thuộc tập hợp đó.
Kí hiệu o cho toán tử là chung chung ở chỗ nó có thể là phép cộng, phép nhân, hoặc bất kì toán tử nào khác.
110. Tính kết hợp là gì?
Nếu a, b, c là các phần tử thuộc một tập hợp, thì kết hợp được cho đúng nếu
a o (b o c) = (a o b) o c
Dấu ngoặc ở đây đơn giản có nghĩa là các phần tử bên trong chúng được ưu tiên xử lí trước.
Ví dụ, nếu toán tử o là kí hiệu cho phép cộng, và các phần tử là số, thì các số trong ngoặc phải được cộng trước.
Như vậy 2 + (3 + 4) = (2 + 3) + 4, nghĩa là
2 + 7 = 5 + 4 phải đúng.
Toán học – Những điều kì thú và những mốc son lịch sử
A.L. Audichya
Trần Nghiêm dịch
Phần tiếp theo >>