Ví dụ thứ hai của tính trơn đã được quan sát thấy cho vũ trụ hiện nay thì khác nhưng có một nét tương đồng với ví dụ thứ nhất ở chỗ nó là một tính chất của vũ trụ hiện nay mà, khi chúng ta ngoại suy ngược dòng thời gian, nó có vẻ hết sức khó hiểu trong ngữ cảnh của lí thuyết Big Bang.
Như đã nói ở Chương 1, cơ sở toán học của vũ trụ giãn nở được cung cấp bởi thuyết tương đối rộng kết hợp với các giả thuyết đẳng hướng và đồng nhất cấu thành nên nguyên lí vũ trụ học. Từ đây dẫn tới một phương trình vi phân đơn giản cho sự phụ thuộc thời gian của hệ số tỉ lệ (đã nói).
--
Phương trình này cho chúng ta biết rằng số phận tối hậu của vũ trụ có vẻ tùy thuộc vào mật độ toàn phần của vật chất và năng lượng trong vũ trụ. Tất nhiên, chúng ta chỉ đang nói tới mật độ trung bình, chứ không phải mật độ cục bộ, nơi có các cấu trúc như thiên hà và sao. Có một giá trị tới hạn cho mật độ này để cho vũ trụ giãn nở mãi mãi nhưng mỗi lúc một chậm đi và cuối cùng thì dừng lại sau một thời gian dài vô hạn. Với mật độ tới hạn này, một quan điểm khác cho rằng động năng dương của chuyển động của các thiên hà và vật chất khác trong vũ trụ cân bằng chính xác với năng lượng hấp dẫn đi cùng với lực hút hấp dẫn. Năng lượng được bảo toàn nên điểm chết tự nhiên là lúc các thiên hà nằm yên và cách nhau vô hạn, và do đó không có lực hút hấp dẫn tàn dư nào nữa.
Nếu mật độ của vũ trụ nhỏ hơn mật độ tới hạn này, thì hình dạng của vũ trụ có độ cong âm và nó sẽ giãn nở mãi mãi mà không có điểm dừng. Vũ trụ độ cong âm này trong chuyên môn được gọi là vũ trụ mở. Trường hợp khả dĩ còn lại là mật độ của vũ trụ lớn hơn mật độ tới hạn, vũ trụ có độ cong dương. Trong vũ trụ đó, pha giãn nở cuối cùng sẽ dừng lại, sau đó là pha co lại, cuối cùng là một Vụ Co Lớn. Nói cách khác, với một vũ trụ đóng như thế thì năng lượng hấp dẫn lớn hơn động năng của các chuyển động. Những lập luận đơn giản này bỏ qua sự rắc rối do năng lượng tối mang đến. Chúng ta sẽ còn trở lại vấn đề này.
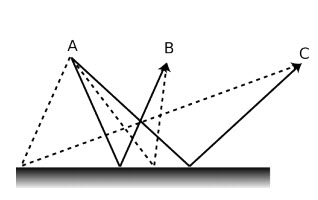
Trường hợp đặc biệt trong đó mật độ của vũ trụ bằng mật độ tới hạn nằm tại ranh giới giữa vũ trụ đóng và vũ trụ mở và được gọi là vũ trụ phẳng. Ba dạng hình học khác nhau có thể được đặc trưng bởi tổng số đo ba góc của một tam giác là nhỏ hơn, lớn hơn hay bằng 180 độ. 180 độ là tổng số đo ba góc của tam giác trong hình học phẳng, còn gọi là hình học Euclid – loại hình học đơn giản nhất được giảng dạy trong nhà trường và đã được biết rất rõ từ thời văn minh Hi Lạp cổ đại. Hai trường hợp kia là ví dụ của hình học phi Euclid, được các nhà toán học khám phá vào thế kỉ 19. Một ví dụ của độ cong dương là một mặt cầu ví dụ như Trái đất. Vẽ một tam giác với một đỉnh tại cực Bắc và hai đỉnh kia nằm trên xích đạo, cách nhau một phần tư vòng tròn xích đạo, ta thu được tam giác có ba góc vuông và tổng số đo ba góc là 270 độ. Tổng lớn hơn 180 độ đặc trưng cho độ cong dương như trong trường hợp vũ trụ đóng. Với độ cong âm như trong trường hợp vũ trụ mở, tổng số đo ba góc của một tam giác nhỏ hơn 180 độ.
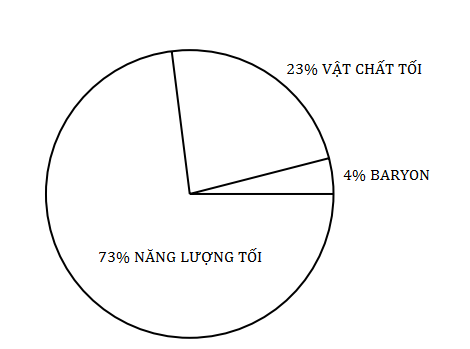
Mật độ khối lượng và năng lượng toàn phần hiện nay bằng với mật độ tới hạn với sai số hai phần trăm. Nói cách khác, ba góc trong một tam giác bất kì cộng lại thật sự bằng 180 độ, với độ chính xác khá tốt. Thực tế này rất bất ngờ trong lí thuyết Big Bang và nó đề xuất có cái gì đó đang còn thiếu. Tại sao vậy?
--
Trong các phương trình mô tả sự tiến hóa của hệ số tỉ lệ, hình học phẳng là một nghiệm không bền. Điều này có nghĩa là nếu vũ trụ hiện nay là phẳng, thì nó rất có khả năng luôn luôn là phẳng. Các sai lệch khỏi tính phẳng hoặc theo hướng đóng hoặc theo hướng mở nhanh chóng được khuếch đại khi vũ trụ giãn nở. Để là gần như phẳng như hiện nay, mật độ lúc một giây sau Big Bang phải bằng mật độ tới hạn đến sai số một phần một trăm nghìn tỉ.
