Trở lại bàn tiệc
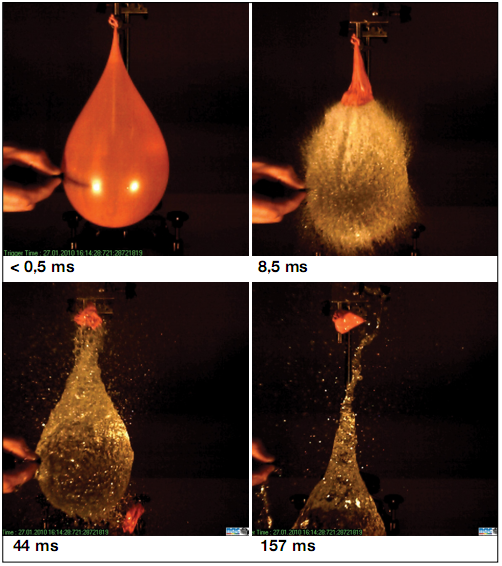
Vấn đề đối với mô hình của Gandy – và nguyên nhân tại sao dự án vật lí kĩ thuật số ban đầu bị thất bại – rút lại là một thứ: vật lí lượng tử. Để tìm hiểu nguyên do, chúng ta hãy trở lại buổi tiệc tối tại nhà hàng Pháp, nơi thức ăn đang bắt đầu nguội lạnh.
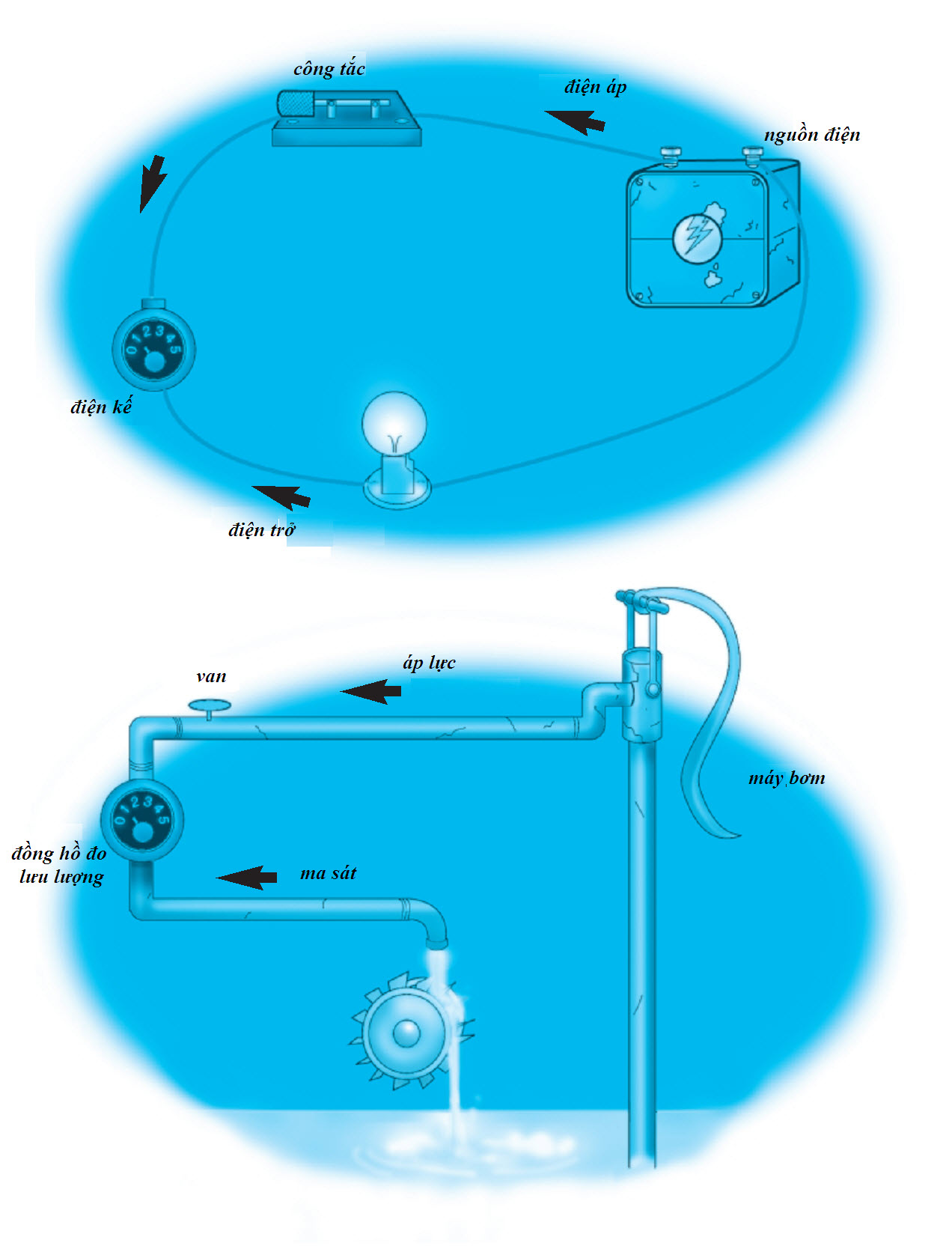
Dựa trên óc phán xét tốt hơn của bạn, bạn đưa ra một lời giải thích của thuyết lượng tử sử dụng dao và nĩa trên bàn ăn. Giờ thì bạn nghe chính mình đang nói “Chọn một hệ có thể là một trong hai thứ - giống như bộ đồ ăn này, nó có thể là một con dao hoặc một cái nĩa.” Bạn đặt con dao và cái nĩa trên bàn với tay cầm của chúng chạm nhau góc 90 độ, tạo thành trục x và trục y của một không gian 2D. “Vâng, theo thuyết lượng tử, dụng cụ dao kéo này không phải là cái này hoặc cái kia. Những trạng thái có thể có là toàn bộ bàn ăn. Chẳng hạn, nó có thể ở đây,” bạn vừa nói vừa thọc tay lên bàn. Nhưng mặc dù rõ ràng bạn đang chạm tay vào bàn ăn tại điểm biểu diễn trạng thái chồng chất 1/√2 |dao〉 + 1/√2 |nĩa〉, nhưng bạn cảm thấy có lẽ khán giả của mình không hiểu hết những ngụ ý bên trong. Bạn cân nhắc đến một lời giải thích khác liên quan đến cái nghiền muối và tiêu, nhưng trước khi bạn có thể bắt đầu, thì người phục vụ mang đến thực đơn tráng miệng rồi.

Dụng cụ ăn có thể cầm trên tay nhưng không lí tưởng để chứng minh thuyết lượng tử. (Ảnh: iStockphoto.com/binabina)
Nguyên nhân chúng ta không bắt gặp sự chồng chất của dao và nĩa trong cuộc sống hàng ngày là hễ khi người ta quan sát một hệ lượng tử thì nó lại trở thành hệ cổ điển. Điều này có nghĩa là đơn vị nhỏ nhất của thông tin lượng tử, gọi là “qubit”, chỉ có thể lưu trữ một bit thông tin cổ điển: 0 hoặc 1, dao hoặc nĩa. Theo ý nghĩa đó, nguyên lí mật độ thông tin hữu hạn của Gandy vẫn tương thích với thuyết lượng tử. Tuy nhiên, như chúng ta nhìn thấy trong nhà hàng, trước khi người ta quan sát một qubit, nó được phép ở trong bất kì sự chồng chất nào của các trạng thái. Vì thế, đó không còn là trường hợp mỗi khối lập phương của không gian có thể được mô tả đầy đủ bằng thông tin hữu hạn chứa trong nó, và đây là chỗ lập luận của Gandy thất bại.
Những hi vọng vật lí học kĩ thuật số có thể hồi sinh lại ở dạng nào đó phát sinh hồi đầu thập niên 1980, khi Richard Feynman đề xuất rằng khoảng trống hiển nhiên giữa công suất và lượng thông tin của thuyết lượng tử và của máy vi tính cổ điển có thể được nối lại bằng một loại máy vi tính mới. Ý tưởng của ông ra đời từ chỗ chứng kiến các máy vi tính cổ điển mất hàng tuần để mô phỏng những thí nghiệm vật lí lượng tử xảy ra nhanh hơn một cái chớp mắt. Qua trực giác, ông cảm thấy công việc mô phỏng những hệ lượng tử có thể được làm tốt hơn bởi một máy vi tính tự nó là một hệ lượng tử.
Giống như những đối tác cổ điển của chúng, máy vi tính lượng tự gồm những mạch điện tạo nên. Để xây dựng mạch lượng tử bạn cần có dây lượng tử, chúng là cái tương tự của dây dẫn thực tế mang những bit thông thường (dưới dạng điện áp), chỉ khác là chúng mang các qubit. Có nhiều cách khác nhau triển khai các qubit và dây trên thực nghiệm; một ví dụ là sử dụng hai trạng thái spin của một hạt nhân nguyên tử spin bán nguyên làm trạng thái qubit, và xử lí chúng bằng sự cộng hưởng từ hạt nhân. Nhưng bạn còn cần có những cổng lượng tử có thể áp dụng cho những dây này. Chẳng hạn, người ta có thể tưởng tượng rằng nó có thể có ích để biến đổi một qubit ở trạng thái |0〉 sang trạng thái chồng chất 1/√2 |0〉 + 1/√2 |1〉 như đã nói. Một dụng cụ thực hiện phép toán này được gọi là cổng Hadamard. Bạn còn cần ít nhất một cổng hai qubit; một ví dụ là cổng điều khiển π/8, nó gây ra một sự biến đổi pha chung nếu cả hai qubit ở trạng thái |1〉 và giữ chúng không thay đổi trong những trường hợp còn lại. Hai cổng qubit này là chung: bằng cách kết hợp chúng, người ta có tính toán bất kì thuật toán lượng tử nào – giống hệt như người ta có thể sử dụng các cổng cổ điển ví dụ như cổng NAND hai bit (luôn luôn trả lại giá trị “true” trừ khi cả hai input đều là true) để tính bất kì thuật toán cổ điển nào.
Hướng đến máy tự động ô lượng tử
Hơn một thập niên qua, các nhà thực nghiệm thuộc nhiều nhóm nghiên cứu trên khắp thế giới đã triển khai thành công những dây lượng tử và những cổng một-qubit ví dụ như cổng Hadamard vừa mô tả ở trên. Những khó khăn thật sự nằm ở sự chính xác của các cổng hai-qubit và việc bảo vệ nhiều dây lượng tử trước môi trường – hãy nhớ rằng, nếu môi trường “quan sát” các dây lượng tử, thì chúng lại trở thành cổ điển.
Làm việc với Gilles Dowek, vừa xây dựng trên những kết quả nghiên cứu trước đó với Vincent Nesme và Reinhard Werner, một trong hai chúng tôi (PA) đã phát triển một phiên bản của giả thuyết Gandy giải thích những sự phức tạp của cơ học lượng tử. Chủ yếu giả thuyết của chúng tôi thay thế nguyên lí mật độ hữu hạn của Gandy bằng một giả thuyết rằng một thể tích hữu hạn của không gian chỉ có thể chứa một số hữu hạn qubit. Việc xem xét những hàm ý của ba nguyên lí mới cập nhật đó đã đưa chúng tôi đến một quan điểm rằng vũ trụ hành xử giống như một phiên bản lượng tử của máy tự động ô đã nói ở phần trước.
Một máy tự động ô lượng tử rất giống với máy tự động ô cổ điển, ngoại trừ là bây giờ các ô trong mạng lưới đó chứa các qubit. Sự diễn tiến thời gian từ thời điểm t đến t +1 trong mô hình này thu được bằng cách áp dụng lặp đi lặp lại một toán tử cổng lượng tử cho láng giềng của các ô, trên khắp không gian. Tuy nhiên, có một số cái tinh vi với máy tự động ô lượng tử không thể nào giải thích khá dễ dàng trong một bức tranh được. Ví dụ, các ô bây giờ có thể ở trong một sự chồng chất của các trạng thái, và chúng còn có thể bị vướng víu với bất kì ô nào đó khác.
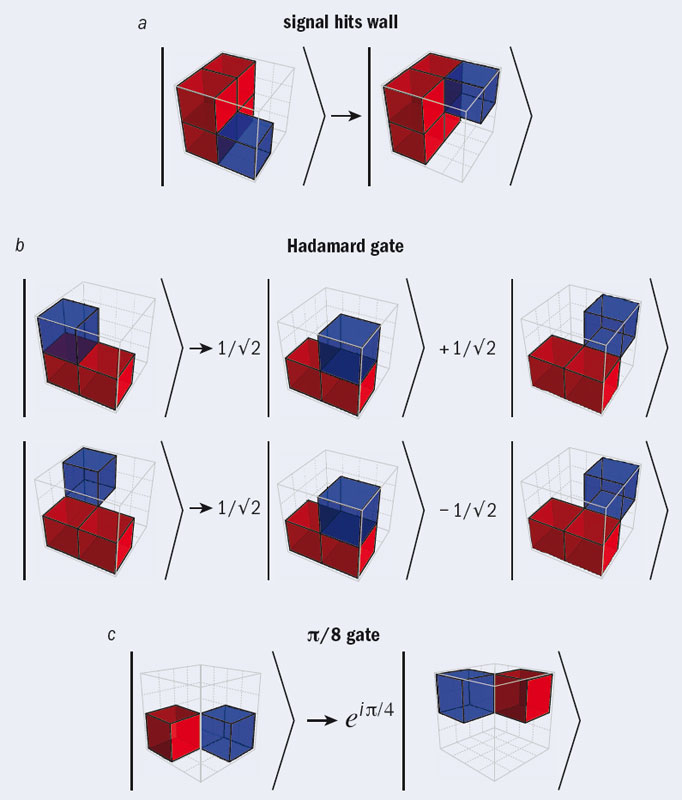
Hình 2. Quy tắc của Trò chơi Lượng tử Cuộc sống được cho bởi một cổng lượng tử tác dụng lên một khối lập phương 2 × 2 × 2 ô láng giềng. Những trường hợp hấp dẫn nhất được minh họa ở đây. (a) Một tín hiệu đi tới một tường gồm bốn ô “đầy” màu đỏ. Dưới nhưng trường hợp này, tín hiệu màu xanh (tô màu chỉ mang tính minh họa – nó còn là một ô “đầy”) sẽ “phản xạ” khỏi tường và đổi chiều theo một trục. Hành trạng này cho phép triển khai các dây lượng tử, kể cả việc nối dây lại và kết hợp các cổng. (b) Một tín hiệu đi tới một tường trên rìa của nó (nói cách khác, một tín hiệu đi tới tường chỉ có hai ô màu đỏ trong vùng lân cận) sẽ phản xạ trong sự chồng chất của hướng trái và hướng phải. Trường hợp này hiện thực hóa cổng Hadamard. (c) Khi hai tín hiệu, ở đây tô màu đỏ và màu xanh, đi chéo qua nhau, pha phức của trạng thái lượng tử đó bị biến đổi, thực hiện một cổng điều khiển π/8.
Một thí dụ hay của máy tự động ô lượng tử là “Trò chơi Lượng tử Cuộc sống” 3D mà chúng tôi đề xuất, chúng tôi đặt tên cho nó theo tên gốc nổi tiếng của Conway. Ở máy tự động ô lượng tử này, mỗi ô lập phương có thể là |rỗng〉, |đầy〉 hoặc bất kì sự chồng chất nào của hai trạng thái qubit này, ví dụ như 1/√2 |đầy〉 – 1/√2 |rỗng〉. Hành trạng của hệ khi nó diễn tiến theo thời gian có thể thu được bằng cách áp dụng một cổng lượng tử cho một mạng lưới lập phương 2 × 2 × 2 (hình 2). Cổng lượng tử địa phương này xác định “luật chơi”.
Tất nhiên, có một khoảng trống lớn giữa việc xây dựng một máy tự động ô lượng tử “mô hình đồ chơi” và việc áp dụng những bài học từ nó cho thế giới thực. Nhưng nếu những phiên bản cập nhật của các giả thuyết Gandy vẫn đúng – và chúng ta thật sự có thể mô tả vũ trụ dưới dạng một máy tự động ô lượng tử khổng lồ - thì việc nghiên cứu vật lí trở thành một trò chơi gắng sức suy luận ra “chương trình” của cỗ máy vi tính khổng lồ, song song mà chúng ta sống trong đó.
Cách tiếp cận thông thường để suy luận ra chương trình đó, tất nhiên, không phải là sử dụng máy tự động ô hoặc bất cứ cái gì giống như chúng, mà là khảo sát “các quy tắc chơi” với những thí nghiệm vật lí ngày một tinh vi hơn, ví dụ như những thí nghiệm tiến hành bằng Máy Va chạm Hadron Lớn tại phòng thí nghiệm vật lí hạt CERN. Tuy nhiên, chúng tôi tin rằng có một phương pháp hướng khoa học máy tính khác, một phương pháp cố gắng tìm ra các quy tắc đó theo kiểu suy luận.
Chúng ta có thể bắt đầu quá trình suy luận này bằng cách loại bỏ những quy tắc quá đơn giản, dựa trên cơ sở là chúng ta sống trong một vũ trụ phức tạp. Tiếp theo, chúng ta lưu ý rằng mọi quy tắc đủ phức tạp đều có thể làm cho mô phỏng lẫn nhau. Nói cách khác, nếu quy tắc của một máy tự động ô lượng tử nhất định đủ phức tạp, thì nó có thể mô phỏng mọi loại máy tự động ô lượng tử khác, ngay cả khi những máy tự động khác có những quy tắc hết sức phức tạp. Một máy tự động ô lượng tử có thể thực hiện một mô phỏng được cho là có tính vạn vật nội, một khái niệm chúng ta đã phát triển trong thế giới lượng tử. Vì thế, nếu chúng ta có thể tìm thấy cái đơn giản nhất, một quy tắc vạn vật nội cho một máy tự động ô lượng tử, thì chúng ta có thể dùng nó để tìm phương pháp đơn giản nhất và “tự nhiên” nhất (theo nghĩa tự nhiên làm thế) triển khai hay mô phỏng các hiện tượng vật lí.
Vươn xa hơn vật lí kĩ thuật số lượng tử
Trò chơi Lượng tử Cuộc sống mà chúng tôi vừa mô tả là một máy tự động ô lượng tử vạn vật nội thu nhỏ, nhưng ta vẫn có thể thấy mọi hiện tượng vật lí có thể được mã hóa bằng những khái niệm đã phát triển ở đây hay không. Nhiều khó khăn vẫn còn trước mắt những ai trong số chúng ta đang cố gắng trả lời câu hỏi “Thiên nhiên tự nó tính toán như thế nào?”. Một trở ngại là các mô hình máy tự động ô lượng tử đó thường không đẳng hướng. Chẳng hạn, trên một mạng lưới ô vuông, các tín hiệu thường có thể truyền đi theo bốn phương nhanh hơn theo đường chéo, nên các mô hình kiểu mạng lưới không thể dễ dàng mô phỏng những đầu sóng kiểu gợn lăn tăn. Một trở ngại nữa là, giống hệt như vật lí học kĩ thuật số cổ điển không dung nạp những đặc điểm khác biệt của thuyết lượng tử, và như thế cần phải được nâng cấp, vật lí học kĩ thuật số lượng tử cũng không dung nạp thuyết tương đối tổng quát, nên nó cũng cần được nâng cấp. Một số thành viên thuộc cộng đồng hấp dẫn-lượng tử, như Alioscia Hamma, Fotini Markopoulou, Simone Severini và Lee Smolin, đã triển khai một số nỗ lực theo hướng này, nên chúng ta có thể đang ở bên bờ của một xu hướng tiến tới nền vật lí kĩ thuật số lượng tử mới, mang tính tương đối luận.
Trong xu thế này, các khái niệm vừa trình bày ở đây, khái niệm máy tự động ô lượng tử và tính vạn vật nội, có khả năng là chìa khóa để tìm kiếm các “mô hình đồ chơi” đơn giản, thu nhỏ và vạn vật. Từ quan điểm khoa học máy tính, việc đạt tới mục tiêu này sẽ gắn liền với việc tìm hiểu bản chất của cỗ máy vi tính lượng tử song song và tương đối tính tối hậu. Nhưng chúng tôi rất biết ơn khi kết luận với một từ cảnh giác: những quan điểm này có lẽ chẳng phải chuyện gì hay ho trong buổi đàm đạo ở nhà hàng. Thật vậy, việc nỗ lực giải thích chúng có thể kết thúc với những người dự tiệc khác cho rằng bạn là người tốt nhất để mời gọi khi lần tới máy vi tính (cổ điển) của họ bị hỏng. Nhưng với một lưu ý tích cực hơn, nếu chúng ta có thể tìm ra các quy tắc thì mọi người đều sẽ là người chiến thắng trong trò chơi cuộc sống này.
- Pablo Arrighi và Jonathan Grattage – Physics World, tháng 6/2012
Trần Nghiêm dịch



![Sách [Light Novel] Dược Sư Tự Sự - Tập 3 - Tặng Kèm Bookmark](https://thuvienvatly.com/images/deals/thumb/sach-light-novel-duoc-su-tu-su-tap-3-tang-kem-bookmark.jpg)