Thời trẻ, Albert Einstein đã mất một năm láng cháng chẳng làm gì. Đâu cứ phải đi đây đi đó mới là ‘lãng phí’ thời gian – thật tiếc, đây lại là cái mà các bậc phụ huynh của con trẻ có xu hướng hay quên. Einstein ở Pavia. Ở Đức, ông bị đuổi học vì không thể chịu nổi sự khắt khe của trường học, ông chuyển qua ở cùng gia đình. Đó là đầu thế kỉ hai mươi, và ở Italy đang bắt đầu cách mạng công nghiệp. Cha của ông, một kĩ sư, đang thi công lắp đặt nhà máy điện đầu tiên trên đồng băng Paduan. Albert đang đọc về Kant và tham dự các buổi thuyết giảng thỉnh thoảng diễn ra tại Đại học Pavia: để cho vui thôi, chứ không thèm ghi danh hay phải nghĩ tới chuyện thi cử. Vâng, đây chính là cách mà các nhà khoa học thực thụ đã ra đời.
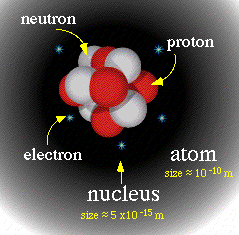
Sau năm này, ông ghi danh tại Viện Bách khoa ở Zurich, và vùi mình vào nghiên cứu vật lí. Một vài năm sau, năm 1905, ông gửi ba bài báo đến tạp chí khoa học danh giá nhất thời ấy, Annalen der Physik (Biên niên Vật lí học). Mỗi một bài báo này đều đáng giá Giải Nobel. Bài thứ nhất chứng minh rằng nguyên tử thật sự tồn tại. Bài thứ hai thiết lập nền tảng đầu tiên cho cơ học lượng tử, lĩnh vực tôi sẽ trình bày trong bài học tiếp theo. Bài thứ ba giới thiệu lí thuyết tương đối thứ nhất của ông (ngày nay gọi là ‘thuyết tương đối đặc biệt’), lí thuyết giải thích làm thế nào thời gian không trôi qua giống hệt nhau đối với mỗi người: hai anh em song sinh y chang nhau sẽ thấy khác biệt tuổi tác, nếu một trong hai người du hành ở tốc độ cao.
Einstein thoắt chốc trở thành nhà khoa học danh tiếng và nhận được vô số lời mời đến làm việc từ các trường đại học. Nhưng có cái gì đó khiến ông không yên: mặc dù được hoan nghênh nhiệt liệt, nhưng lí thuyết tương đối của ông không khớp với cái mà chúng ta đã biết về lực hấp dẫn, tức là cách vạn vật rơi xuống. Rồi ông nhận ra điều này khi đang viết một bài báo tóm tắt lí thuyết của ông, và bắt đầu tự hỏi liệu định luật ‘vạn vật hấp dẫn’ như đã được thiết lập bởi cha đẻ của vật lí học, Isaac Newton, có cần phải hiệu chỉnh để làm cho nó tương thích với khái niệm mới của thuyết tương đối hay không. Ông vùi đầu vào giải quyết vấn đề. Mất mười năm mới xong. Mười năm nghiên cứu điên cuồng, cố gắng, sai sót, lộn xộn, những bài báo lỗi, những ý tưởng sáng giá, những ý tưởng sai lầm.
Cuối cùng, tháng 11 năm 1915, ông gửi in một bài báo đưa ra lời giải đáp hoàn chỉnh: một lí thuyết mới của lực hấp dẫn, cái ông gọi là ‘Thuyết tương đối tổng quát’, kiệt tác của đời ông và là ‘lí thuyết đẹp nhất’, theo nhà vật lí Nga vĩ đại Lev Landau.
Có những kiệt tác tuyệt đối khiến chúng ta hứng khởi: Requiem của Mozart; Odyssey của Homer; Nhà nguyện Sistine; Vua Lear [một vở bi kịch của Shakespear]. Để đánh giá đầy đủ cái thiên tài của chúng có lẽ đòi hỏi một bề dày học thuật, nhưng cái đọng lại là nét đẹp thuần mĩ – và không những vậy, chúng còn khai nhãn cho chúng ta đến một viễn cảnh mới trên thế giới. Viên ngọc quý của Einstein, thuyết tương đối tổng quát, là một kiệt tác thuộc tầm cỡ này.
Tôi còn nhớ cái cảm giác hào hứng của mình khi tôi bắt đầu hiểu ra chút gì đó về thuyết tương đối tổng quát. Đó là vào mùa hè. Tôi đang ở bãi biển Condofuri ở Calabria, tắm nắng Địa Trung Hải ở Hi Lạp, và đó là năm cuối tôi học đại học. Không bị quẫn trí bởi trường lớp, người ta nghiên cứu tốt nhất là trong các kì nghỉ. Tôi đang nghiên cứu với sự hỗ trợ của một quyển sách đã bị lũ chuột gặm rách mép, vì ban đêm tôi thường dùng nó để chặn mấy cái hang của những sinh vật tội nghiệp này trong căn nhà tềnh toàng kiểu hippi trên sườn đồi Umbrian, nơi tôi thường trú ẩn để lánh cái chán ngắt của giảng đường ở Bologna. Thỉnh thoảng, mỗi khi tôi rời mắt khỏi quyển sách và nhìn ngắm biển cả lung linh: dường như tôi thật sự đang nhìn thấy sự cong của không gian và thời gian mà Einstein đã tưởng tượng. Như thể thần kì: như thể một người bạn đang thì thào vào tai tôi một câu thần chú bí ẩn nào đó, bất ngờ vén màn che của thực tại để làm lộ ra một cấp độ đơn giản hơn, sâu sắc hơn. Kể từ khi chúng ta phát hiện Trái đất tròn và quay tròn giống như một con quay điên cuồng, ta hiểu được rằng thực tại không như nó biểu hiện trước chúng ta: mỗi khi ta nhìn vào một phương diện mới của nó, thì đó là một trải nghiệm xúc cảm sâu sắc. Một mạng che nữa đã rơi xuống.
Nhưng trong vô số bước nhảy vọt nhận thức của chúng ta tiếp nối nhau trong tiến trình lịch sử, thì bước nhảy của Einstein có lẽ không có ai sánh bằng. Vì sao vậy?
Trước tiên là bởi vì, một khi bạn hiểu nó vận hành như thế nào, thì lí thuyết tương đối có nét đơn giản một cách khêu gợi. Tôi sẽ tóm tắt ý tưởng.
Newton đã nỗ lực giải thích nguyên nhân vạn vật rơi xuống và hành tinh quay quanh mặt trời. Ông đã tưởng tượng ra sự tồn tại của một ‘lực’ hút mọi vật thể có khối lượng về phía nhau, và gọi nó là ‘lực hấp dẫn’. Làm thế nào lực này tác dụng giữa các vật thể ở xa nhau, không có cái gì ở giữa chúng, thì chẳng rõ – và vị cha đẻ vĩ đại của khoa học hiện đại thận trọng đưa ra một giả thuyết. Newton hình dung các vật thể chuyển động trong không gian, và không gian đó là một bình chứa khổng lồ trống rỗng, một cái hộp to lớn bao trùm cả vũ trụ, một cấu trúc mênh mông trong đó vạn vật chuyển động thẳng cho đến khi có lực cưỡng bức quỹ đạo của nó thành đường cong. ‘Không gian’ này làm bằng cái gì, tức cái bình chứa thế giới mà ông phát minh ra làm bằng cái gì, Newton không nói được. Nhưng một vài năm trước khi Einstein chào đời, hai nhà vật lí vĩ đại người Anh, Michael Faraday và James Maxwell, đã bổ sung thêm một thành phần chủ chốt cho thế giới lạnh lẽo của Newton: đó là trường điện từ. Trường này là một thực thể có thật, nó lan tỏa ở mọi nơi, truyền sóng vô tuyến, chiếm đầy không gian, có thể dao động và nhấp nhô như mặt hồ, và ‘trung chuyển’ lực điện. Từ thuở nhỏ Einstein đã bị mê hoặc bởi trường điện từ làm quay rô-to trong các nhà máy điện mà cha ông xây lắp, và ông sớm nhận thức rằng lực hấp dẫn, giống như lực điện, cũng phải được trung chuyển bởi một trường: phải tồn tại ‘trường hấp dẫn’ tương tự như ‘điện trường’. Ông tập trung tìm hiểu ‘trường hấp dẫn’ này hoạt động như thế nào, và tìm cách mô tả nó bằng các phương trình toán học.
Và chính lúc này một ý tưởng phi thường xảy đến với ông, một cú sét trí tuệ thuần khiết: trường hấp dẫn không lan tỏa trong không gian; mà trường hấp dẫn chính là không gian đó. Đây là ý tưởng của thuyết tương đối tổng quát. ‘Không gian’ của Newton, cái qua đó vạn vật chuyển động, và ‘trường hấp dẫn’ là một và đồng nhất với nhau.
Đó là thời khắc khai sáng. Một sự đơn giản hóa trọng yếu của thế giới: không gian không còn là cái gì đó tách biệt với vật chất, mà nó là một trong những thành phần ‘vật liệu’ của thế giới. Một thực thể lượn sóng, cong gập, uốn éo, xoắn. Chúng ta không sống trong một hạ tầng rắn chắc vô hình: chúng ta đắm mình trong một vỏ ốc mềm dẻo khổng lồ. Mặt trời làm cong không gian xung quanh nó và Trái đất không quay xung quanh mặt trời vì một lực bí ẩn mà chạy thẳng trong không gian bị nghiêng, kiểu như hòn bi lăn trong một cái phễu. Không có những lực bí ẩn phát ra tại tâm phễu; chính bản chất cong của thành phễu làm cho hòn bi lăn đi. Các hành tinh quay tròn xung quanh mặt trời, và vạn vật rơi xuống, là bởi vì không gian cong.
Làm thế nào ta có thể mô tả sự cong này của không gian? Nhà toán học lỗi lạc nhất của thế kỉ mười chín, Carl Friedrich Gauss, người được mệnh danh là ‘ông hoàng toán học’, đã viết ra các công thức toán học mô tả các mặt cong hai chiều, ví dụ như mặt đồi. Sau đó ông yêu cầu một sinh viên năng khiếu của ông khái quát hóa lí thuyết để bao hàm cả không gian ba chiều hoặc nhiều chiều hơn. Chàng sinh viên nhận nhiệm vụ, Bernhard Riemann, đã làm một luận án tiến sĩ ấn tượng thuộc loại trông như hoàn toàn chẳng có ứng dụng gì. Kết luận của luận án của Riemann là các tính chất của một không gian cong được thâu tóm bởi một đối tượng toán học đặc biệt mà ngày nay chúng ta gọi là độ cong Riemann, và kí hiệu nó bằng chữ cái ‘R’. Einstein đã viết một phương trình phát biểu rằng R là tương đương với năng lượng của vật chất. Tức là nói: không gian cong nơi có vật chất. Vậy thôi. Phương trình chiếm nửa dòng, không gì thêm nữa. Một hình dung – không gian cong – trở thành một phương trình.

Nhưng chứa trong phương trình này có một vũ trụ lúc nhúc. Và ở đây sự phong phú kì diệu của lí thuyết tuần tự đưa đến những dự đoán huyền ảo tựa như những câu nói mê sảng của người điên, nhưng hóa ra tất cả đều là đúng.
Trước tiên, phương trình mô tả không gian uốn cong như thế nào xung quanh một ngôi sao. Do sự cong này, không chỉ các hành tinh quay xung quanh ngôi sao, mà cả ánh sáng cũng không còn truyền theo đường thẳng và bị lệch. Einstein dự đoán rằng mặt trời làm cho ánh sáng truyền lệch phương. Năm 1919, sự lệch phương này đã được đo, và dự đoán được xác nhận. Nhưng không phải chỉ có không gian cong; thời gian cũng cong nốt. Einstein dự đoán rằng càng lên cao khỏi mặt đất thời gian càng trôi nhanh hơn. Hiệu ứng này đã được đo và hóa ra là đúng. Nếu một người sống ở mực nước biển gặp lại người anh em song sinh sống trên núi cao, anh ta sẽ thấy người anh em của mình hơi già hơn mình một chút. Và đây mới là khởi đầu câu chuyện thôi.
Khi một ngôi sao lớn thiêu hết chất đốt (hydro) của nó, nó tàn lụi. Cái xác còn lại không còn được chống đỡ của áp suất nhiệt do sự cháy và co lại dưới sức nặng của riêng nó, rồi đến lúc nó bẻ cong không gian đến độ nó rơi vào một cái lỗ thật sự. Đây là những ‘lỗ đen’ nổi tiếng. Lúc tôi còn học đại học, lỗ đen được xem là những dự đoán rất khó tin của một lí thuyết bí truyền. Ngày nay, các nhà thiên văn đã quan sát thấy hàng trăm lỗ đen trên bầu trời, và đã nghiên cứu chúng hết sức chi tiết.
Nhưng chưa hết. Toàn bộ không gian có thể dãn ra và co lại. Hơn nữa, phương trình Einstein cho thấy không gian không thể tĩnh lặng; nó phải đang dãn nở. Năm 1930, sự dãn nở của vũ trụ thật sự được quan sát thấy. Phương trình Einstein dự đoán sự dãn nở đó phải được kích hoạt bởi sự nổ của một vũ trụ non trẻ, cực kì nhỏ và cực kì nóng: cái ngày nay chúng ta gọi là ‘Big Bang’ (Vụ nổ Lớn). Lại một lần nữa, thoạt đầu chẳng ai tin điều này, nhưng bằng chứng tích góp dần cho đến khi bức xạ nền vũ trụ - ánh le lói khuếch tán còn lại từ nhiệt phát sinh bởi vụ nổ ban đầu – thật sự được quan sát thấy trên bầu trời. Dự đoán phát sinh từ phương trình Einstein hóa ra là đúng. Và còn nữa, lí thuyết tương đối cam chắc rằng không gian chuyển động giống như mặt biển. Hiệu ứng ‘sóng hấp dẫn’ này đã được quan sát thấy trên bầu trời ở những ngôi sao đôi, và khớp với dự đoán của lí thuyết đến độ chuẩn xác lạ lùng là một phần triệu tỉ. Và còn nữa.
Tóm lại, lí thuyết tương đối mô tả một thế giới đầy màu sắc và bất ngờ trong đó vũ trụ bùng nổ, không gian co lại thành những cái lỗ không đáy, thời gian chùng lại và chậm đi ở gần một hành tinh, và những khoảng không vô tận giữa các sao thì gợn sóng và nhấp nhô giống như mặt biển... Và toàn bộ những điều này, chúng dần dần hiện ra từ quyển sách bị chuột gặm của tôi, không phải là câu chuyện thêu dệt của thằng ngốc mất trí, chẳng phải ảo giác do cái nắng Địa Trung Hải như thiêu như đốt và mặt biển chói lóa vùng Calabria. Nó là thực tại.
Hay tốt hơn, là một thoáng của thực tại, nó ít nhiều sáng tỏ hơn cái nhìn hàng ngày mờ mờ ảo ảo và vô vị của chúng ta. Một thực tại dường như được làm bằng cùng chất liệu như chất liệu của những giấc mơ, tuy vậy nó lại có thật hơn thế giới mơ mê sảng lờ mờ của chúng ta.
Toàn bộ điều này là kết quả của một trực giác cơ bản: rằng không gian và trường hấp dẫn là cùng một thứ. Và của một phương trình đơn giản mà tôi không thể không viết ra đây, mặc dù bạn hầu như chắc chắn sẽ không thể giải mã được nó. Có lẽ bất cứ ai đang đọc quyển sách này đều có thể thưởng thức nét đẹp tuyệt vời của nó:
Rab − ½ R gab = Tab
Thế thôi.
Tất nhiên, bạn sẽ cần nghiên cứu và tiêu hóa toán học Riemann để làm chủ kĩ thuật đọc và sử dụng phương trình này. Nó cần một chút tận tâm và nỗ lực. Nhưng dẫu cho không biết nhạc lí, bạn vẫn có thể thưởng thức cái đẹp của khúc tấu Beethoven. Trong cả hai trường hợp, phần thưởng là cái đẹp thuần mĩ, và đôi mắt mới để nhìn ngắm thế giới.
♦ Trích Bài học thứ nhất, Sách Bảy Bài học Vật lí Ngắn của Carlo Rovelli
Bản dịch của Trần Nghiêm