Bài này giới thiệu vắn tắt cho bạn đọc những bí ẩn lớn nhất trong Toán học và Vật lý học. Trong các bí ẩn này có cái đã được khám phá, có cái đang trong quá trình thẩm định và nói chung đa phần đang chờ lời giải của các nhà khoa học.
* CÁC BÍ ẨN TRONG VẬT LÝ HỌC
1. Vũ trụ hình thành như thế nào?
Câu hỏi này cho đến nay vẫn chưa có sự trả lời chính xác. Giả thuyết hiện nay được nhiều người biết đến, đó là giả thuyết cho rằng vũ trụ bắt đầu hình thành từ vụ nổ BigBang cách đây 13,7 tỉ năm về trước. Song giả thuyết này chỉ là dự đoán, không kiểm chứng được.
2. Phần còn lại của vũ trụ ở đâu?
Nhiều nghiên cứu của các nhà khoa học đều xác nhận: vũ trụ ngày nay đang nở nhanh hơn trong quá khứ! Từ kết luận này người ta đã đưa đến những suy luận (được công bố vào năm 2003) là: Trong các thành phần vật chất và năng lượng cấu tạo nên vũ trụ thì vật chất và năng lượng thông thường chỉ chiếm khoảng 4%: bao gồm bức xạ 0,005%; vật chất nhìn thấy khoảng 0,5% và vật chất không phát sáng khoảng 3,5%. Còn lại là vật chất tối và năng lượng tối chiếm khoảng 96%. năng lượng tối vẫn còn là bí mật lớn trong Vật lí.
3. Cái gì tạo nên lực hấp dẫn?
Nếu chúng ta nghĩ
Đọc thêm Có boson Higgs trong không gian vũ trụ hay không?
4. Lí thuyết của vạn vật có tồn tại không?
Người ta hi vọng có một lý thuyết cho vạn vật. Nhưng cho đến nay ý nghĩ này vẫn còn là điều bí ẩn. Các nhà Vật lý đã xây dựng được mô hình chuẩn. Mô hình chuẩn không giải thích được vấn đề về lực hấp dẫn. Mô hình chuẩn lại không đúng với các phần năng lượng cao.
5. Người ngoài hành tinh có tồn tại không?
Hệ Mặt Trời mà trong đó có Quả Đất của chúng ta là một trtong các hành tinh có sự sống. Mặt Trời là một ngôi sao phát sáng trong hàng tỉ tỉ các ngôi sao phát sáng khác trong vũ trụ. Theo suy luận sẽ có những hành tinh nào đó của một ngôi sao phát sáng nào đó giống như Quả Đất của chúng ta với Mặt Trời sẽ tồn tại sự sống, có tồn tại người ngoài hành tinh!? Suy luận và hi vọng này cho đến nay vẫn chưa có lời giải đáp. Vũ trụ vẫn là bí ẩn.
Những vòng tròn ma trên đồng lúa luôn khiến người ta nghĩ đến người ngoài hành tinh. Đọc thêm Bí ẩn những vòng tròn ma trên đồng lúa
* CÁC BÍ ẨN TRONG TOÁN HỌC
7 bí ẩn lớn nhất trong Toán học (hay còn gọi là 7 bài toán Clay) do các nhà toán học của viện Clay (CMI) Mĩ chọn lọc đưa ra và phần thưởng 1 triệu USD cho ai khám phá ra 1 trong 7 bí ẩn này:
1. Giả thuyết Poincare
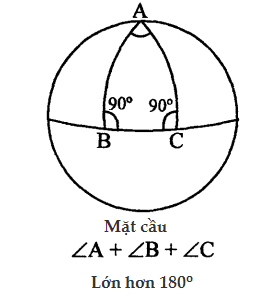
Giả thuyết này được nhà toán học người Pháp Henri Poincare đưa ra năm 1904. Có thể vắn tắt giả thuyết như sau: "một đa tạp 3 chiều Compắc không có biên là đơn liên, thì nó đồng phôi với mặt cầu 3 chiều". Giả thuyết cho đa tạp n chiều chính là giả thuyết Poincare mở rộng. Vào cuối thập niên 70 của thế kỉ XX nhà bác học Mĩ William Thurston trong quá trình nghiên cứu những vấn đề có liên quan đến giả thuyết Poincare, ông đã tổng quát hoá thành một chương trình, người ta gọi là giả thuyết hình học hoá, nó chứa giả thuyết Poincare như một trường hợp riêng. Chương trình này gọi là chương trình Haminlton. Giải quyết triệt để bài toán này là nhà toán học lừng danh người Nga (gốc Do Thái) Grigory Perelman sinh năm 1966. Ông đã khám phá bí ẩn này vào năm 2002 và đến năm 2006 mới được các nhà toán học kiểm tra thừa nhận. Cũng chú ý rằng Grigory Perelman đã từ chối nhận giải thưởng Fields và phần thưởng 1 triệu USD.
2. Giả thuyết Riemann trong lí thuyết số
Các số nguyên tố giữ vai trò trung tâm trong số học. Sự phân chia các số này nó liên kết chặt chẽ với hàm số Euler. Năm 1850 nhà toán học người ĐứcBemard Riemann đã đưa ra giả thuyết: "các giá trị không phù hợp với hàm số Euler được sắp xếp theo thứ tự".
Các nhà toán học đã kiểm tra tính đúng đắn của giả thuyết này trong 1500 triệu giá trị đầu tiên, nhưng vẫn không chứng minh triệt để được giả thuyết. Một thông tin gần đây cho biết vào tháng 6 năm 2004 nhà toán học người Pháp Louis De Branges đã công bố công trình chứng minh giả thuyết này, nhưng cho đến nay công trình vẫn đang trong giai đoạn kiểm tra tính đúng đắn.
Đọc thêm: Thêm một nhà toán học đoạt giải thưởng triệu đô
3. Giả thuyết Hodge trong hình học đại số
Năm 1950 nhà toán học người Anh William Hodge đã nêu giả thuyết mang tên ông. Ta có thể hình dung như sau: người ta thấy rằng các khái niệm trong hình học như đường thẳng, đường cong, đường tròn... đã bị thay thế bởi các khái niệm đại số hiệu quả và khái quát hơn; các hình không gian đang dần dần đi tới hình học của tính đồng đẳng. Việc mở rộng các khái niệm đã dẫn đến bản chất hình học biến mất trong toán học. William Hodge đã đưa ra giả thuyết với nội dung: "trong một số dạng không gian, các thành phần của tính đồng đẳng sẽ tìm lại bản chất hình học của chúng...". Giả thuyết này cho đến nay chưa ai chứng minh được.
4. Giả thuyết Birch và Swinnerton-Dyer trong hình học đại số và lí thuyết số
Vào thập niên 60 của thế kỉ XX các nhà toán học người Anh là Bryan Birch; Petơrswinnerton-Dyer đã đưa ra giả thuyết có nội dung: "đối với nhóm phương trình có đồ thị là các đường cong elip loại 1 thì số nghiệm của phương trình phụ thuộc vào một hàm số f. Nếu hàm số f triệt tiêu tại giá trị bằng 1, ( f(1) = 0) thì phương trình có vô số nghiệm, nếu không số nghiệm là hữu hạn". Giả thuyết này vẫn chưa chứng minh được.
5. Bài toán P = NP
Bài toán này được nhà toán học Canada Stephen cook đưa ra năm 1971. Có thể hiểu vắn tắt bài toán như sau: gọi tập hợp những vấn đề mà người ta thẩm tra kết quả dễ hơn là tập hợp P; và tập hợp những vấn đề mà người ta dễ tìm ra hơn là tập hợp NP. Hãy chứng minh P = NP? Bí ẩn này cũng đang thách thức các nhà khoa học.
6. Số nghiệm của các phương trình Yang-Mills
Hai nhà khoa học Mĩ là Chen nin Yang (Dương Chấn Ninh) và Robert Mills đã đưa ra các phương trình mang tên hai ông vào năm 1950. Các phương trình này đã biểu diễn mối quan hệ mật thiết giữa Vật lý về hạt cơ bản với hình học của các không gian sợi, nó cũng cho thấy sự thống nhất của hình học với phần trung tâm của thế giới lượng tử. Tuy nhiên đến giờ người ta chưa xác định chính xác số nghiệm của các phương trình và bài toán trở thành 1 trong 7 bí ẩn của Toán học.
7. Phương trình Navier - Stokes trong phương trình đạo hàm riêng
Vào thế kỉ thứ XIX hai nhà khoa học Henri Navier và George Stokes đã vận dụng các định luật về chuyển động của Newton vào chất lỏng và chất khí để thiết lập nên các phương trình có tên gọi Navier - Stokes nhằm mô tả hình dạng của sóng, chuyển động của khí quyển, xoáy lốc không khí và cả hình thái các Thiên Hà ở thời điểm nguyên thuỷ của vũ trụ. Các phương trình này cho đến nay vẫn là điều bí ẩn bởi vì người ta chưa giải được, chưa xác định chính xác số nghiệm, thậm chí còn không biết phương trình có nghiệm hay không.
Đọc thêm 7 phương trình chi phối cuộc sống của chúng ta - Phần 1
Tài liệu tham khảo: Tạp chí Vật lí Ngày nay các số 48;51;60;64;66;72;74;79;80;97;99;100
Trương Văn Thanh - Thuvienvatly.com
GV chuyên Vật Lý tại Thanh Hóa
