Vũ trụ mở
Một Vũ trụ được nói là mở nếu nó không chứa đủ vật chất để làm nó ngừng giãn nở6. Trong trường hợp này, mọi thứ hơi khó hình dung hơn chút. Trước tiên, vì loại vũ trụ này không đóng kín lên nó, nên cách duy nhất để nó không có biên giới là nó phải vô hạn7. Hình dạng đơn giản nhất mà một vũ trụ như thế có thể có là vật tương tự phẳng, ba chiều của tấm cao su sẽ giãn ra vô hạn về mọi hướng. Nhưng để cho một Vũ trụ không có độ cong gì hết sẽ là một trường hợp rất đặc biệt. Nó giống như ví dụ quả cầu lăn lên dốc và lên tới đỉnh thì hết hơi và không còn năng lượng để tiếp tục lăn trên cái đỉnh bằng phẳng nữa. Có khả năng hơn nhiều, nếu nó không lăn xuống trở lại, là nó sẽ còn một phần năng lượng để tiếp tục lăn trên đỉnh. Một vũ trụ tương ứng với một kịch bản như vậy sẽ không phẳng mà bị cong. Tuy nhiên, lần này chúng ta nói nó có độ cong âm.
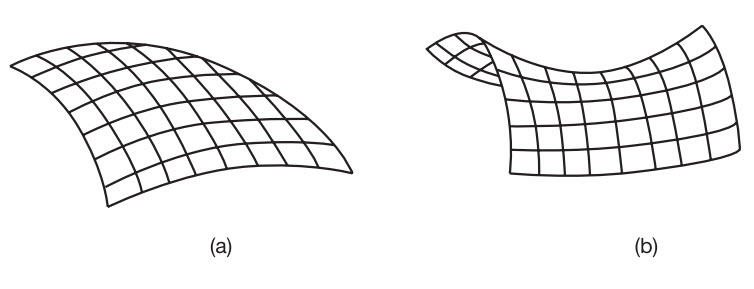
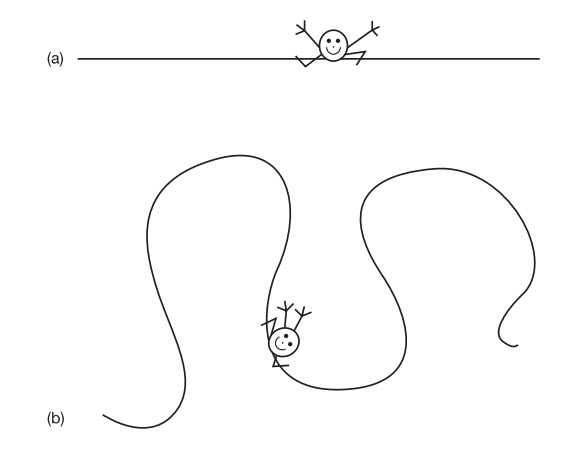
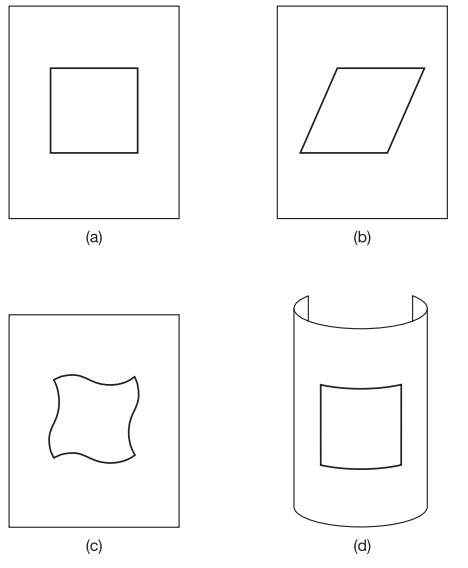
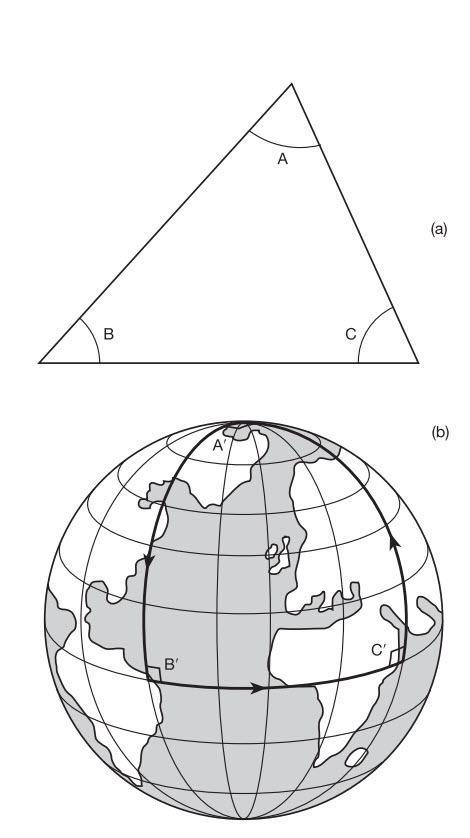
Hình 3.2 Không gian 2D cong dương (a) và âm (b)
Vì thế, bằng cách bỏ đi một trong các chiều không gian, chúng ta có thể nói tới những kiểu cong khác nhau mà Vũ trụ có thể có. Nếu một vũ trụ cong dương, trong một chiều thấp hơn, tương ứng với bề mặt của một quả cầu và một vũ trụ phẳng tương ứng với một tấm phẳng hai chiều, thì một mặt cong âm hai chiều có hình dạng ra sao? Hình dạng này thật không đơn giản. Tên gọi toán học chính xác cho một hình dạng như thế là một hyperboloid thuận, hay mặt hyperbolic và không thể hình dung ra chính xác. Nói đại khái, nó hình dạng của một cái yên ngựa (xem Hình 3.2). Sự khác biệt giữa độ cong dương của một quả cầu và độ cong âm của hình yên ngựa là ở chỗ, trong khi ở quả cầu hai đường đi bất kì trên bề mặt cắt vuông góc nhau thì cong theo cùng một chiều, thì những đường đi như vậy trong trường hợp hình yên ngựa sẽ cong theo hai chiều ngược nhau. Và lí do cái yên ngựa không phải là mô tả chính xác của mặt hyperbolic là ở chỗ khi bạn càng tiến ra xa tâm của cái yên ngựa thì bề mặt càng phẳng đi, trong khi đối với một hyperboloid thuận. bề mặt đó phải cong đều ở mọi nơi. Không thể kéo căng một bề mặt như thế.
Vì hình dạng của một vũ trụ mở là cái gì đó rất khó hình dung, thậm chí ở một chiều thấp thôi, nên chúng ta hãy thử xem chúng ta có thể làm gì tốt hơn không ở việc tìm hiểu một chi tiết khó hiểu khác. Đó là, nếu Vũ trụ là mở và vô hạn thì nó giãn nở thành cái gì? Với từ vô hạn, ở đây tôi muốn nói không gian trải ra mãi mãi theo mọi hướng. Dường như nó chẳng thể nào giãn ra được chút nào nữa vì toàn bộ không gian đã sử dụng hết và nằm gọn bên trong Vũ trụ đó rồi. Một lần nữa, chúng ta có thể nhìn nhận vấn đề rõ ràng hơn trong không gian hai chiều. Trong trường hợp vũ trụ đóng (bề mặt của quả khí cầu), chúng ta có thể tưởng tượng sự giãn nở tỏa ra vào một chiều cao hơn, nhưng đối với một tấm phẳng có một diện tích vô hạn, thì sự giãn nở sẽ luôn luôn ở trong mặt phẳng tấm đó, và chúng ta không thể sử dụng chiều thứ ba (bên ngoài tấm đó) làm nơi cho nó giãn nở vào.
Để giải quyết vấn đề này, tôi cần giải thích một chút toán học. Chẳng ai dễ chịu khi nghĩ tới sự vô hạn. Tôi nhớ lúc nhỏ từng được nghe kể rằng khi chúng ta chết, chúng ta đi lên Thiên đường và ở trên đó mãi mãi. Suy nghĩ này khiến tôi thất vọng vì tôi không muốn nghĩ tới cái gì đó chỉ diễn ra mà không hề có sự kết thúc nào cả. Bất chấp sự khó khăn mà đa số chúng ta vấp phải khi xử lí sự vô hạn, một số nhà toán học đã dành cả đời để nghiên cứu nó. Thật vậy, thậm chí có nhiều loại vô hạn khác nhau nữa.
Hãy nghĩ tới dãy số nguyên 1, 2, 3, 4… kéo dài mãi mãi. Chúng ta nói rằng có một số vô hạn số nguyên. Nhưng còn dãy số chẵn 2, 4, 6, 8… thì sao? Chắc chắn dãy này cũng kéo dài vô hạn. Và vì nói chung có lượng số nguyên nhiều gấp đôi lượng số chẵn, nên chúng ta có hai vô hạn dường như lớn gấp đôi nhau. Còn tất cả những con số, chứ không nguyên thì sao? Chẳng hạn, chúng ta hãy xét những con số
0; 0,1; 0,2; 0,3;…; 0,9; 1,0; 1,1; 1,2; 1,3;…
và cứ thế đến vô hạn. Dãy vô hạn này chứa mười phần tử so với mỗi phần tử trong dãy số nguyên. Vì thế, phải chăng số lượng vô hạn những phần tử này gấp 10 lần số lượng vô hạn những con số nguyên? Trong toán học, có cả một phân ngành dành riêng cho nghiên cứu sự vô hạn. Hóa ra ba dãy số ở trên đều cùng thuộc một loại vô hạn. Nhưng còn có những loại khác nữa. Xét những dãy gồm tất cả những con số (gọi là tập hợp số thực) bao gồm hết mọi phân số nằm giữa các giá trị nguyên. Ngay cả khoảng giữa hai số nguyên liên tiếp như 0 và 1 cũng sẽ chứa vô hạn số (0;…; 0,00103;…; 0,36252;…; 0,9997;…; 0,999999;…; 1) vì chúng ta luôn luôn có thể nghĩ ra một phân số mới chèn ở giữa, tuy nó có thể có nhiều chữ số thập phân. Tương tự như vậy, sẽ có vô hạn phân số nằm giữa 1 và 2, giữa 2 và 3, và giữa 763 và 764, và vân vân. Như vậy, chúng ta có một tập hợp chứa vô hạn số nguyên và vô hạn phân số nằm giữa những số nguyên liên tiếp. Sự vô hạn toàn bộ như thế này thì “mạnh” hơn nhiều so với sự vô hạn của những số nguyên, mặc dù cả hai đều không bao giờ kết thúc! Hóa ra trên thực tế có một số vô hạn những vô hạn khác nhau!
Toàn bộ vấn đề này đưa chúng ta đến đâu? Nhà vũ trụ học Igor Novikov, mà nhiều người xem là câu trả lời của nước Nga cho Stephen Hawking, đã sử dụng khái niệm những vô hạn khác nhau để giải thích một vũ trụ vô hạn vẫn có thể giãn ra như thế nào. Hãy tưởng tượng bạn đi vào Khách sạn Vô hạn, nơi có vô số phòng – tôi đã từng ở trong một số khách sạn gần gần như thế, và có mấy lần tôi gần như đã bị lạc. Bạn được biết tại sảnh tiếp tân rằng họ rất bận vào ban đêm và có số vô hạn khách nên tất cả các phòng đều đã có người. Bạn phàn nàn với người quản lí rằng bạn đã đặt chỗ trước và cố nài họ dành cho bạn một phòng trong đêm đó. “Không hề gì”, người quản lí nói, “trong Khách sạn Vô hạn luôn luôn có sẵn phòng cho khách đến sau”. Sau đó, họ cho chuyển người ở phòng 1 sang phòng 2, người ở phòng 2 sang phòng 3, và cứ thế cho đến vô hạn. Và sau đó bạn được nhận phòng số 1.
Vậy nếu số vô hạn khách đến cùng một lúc thì sao? Vẫn không vấn đề gì (hãy quên đi thời khắc dãy người dài xếp hàng tại quầy tiếp tân nhé). Ban quản lí giờ cho chuyển người ở phòng 1 sang phòng 2, người ở phòng 2 lúc đầu sang phòng 4, người ở phòng 3 sang phòng 6, 4 sang 8, và vân vân, cho đến khi toàn bộ khách đã chuyển phòng xong. Giờ thì toàn bộ những phòng số chẵn đã có người. Vì có số vô hạn những phòng như thế này nên toàn bộ khách ban đầu đã được bố trí chỗ nghỉ. Sự sắp xếp này để lại số vô hạn những căn phòng số lẻ còn bỏ không và dành sẵn cho khách mới đến.
Chúng ta có thể liên hệ những người khách ở khách sạn này với không gian bị chiếm giữ bởi một vũ trụ vô hạn. Cho dù những người khách mới đến vào lúc nào cũng vậy. Khách sạn, là vô hạn, luôn luôn có thể đáp ứng phòng nghỉ cho họ. Theo kiểu giống như vậy, một không gian vô hạn luôn luôn có thể giãn ra.
Giờ thì có lẽ chúng ta đã tiến tới một đặc điểm lộn xộn nhất của một vũ trụ vô hạn. Nếu cái gì đó đang tăng dần về kích cỡ, thì theo định nghĩa nó sẽ mãi mãi trở nên vô hạn. Như vậy, nếu Vũ trụ của chúng ta là vô hạn về kích cỡ ngày nay thì nó cũng phải là vô hạn trong quá khứ. Thật vậy, nó phải vô hạn về kích cỡ tại thời điểm Big Bang! Điều này thật sự nằm ngoài khái niệm Big Bang là sự kiện khi toàn bộ không gian bị nén xuống một điểm có kích cỡ zero. Khái niệm này ít nhất có thể hình dung ra trong trường hợp một vũ trụ đóng bằng cách giảm đi một chiều và xét ví dụ quả khí cầu. Nhưng một vũ trụ mở không bao giờ có kích cỡ zero. Cách duy nhất nghĩ về vũ trụ này là hãy tưởng tượng Big Bang đã xảy ra ở mọi nơi cùng một lúc trong một vũ trụ đã vô hạn. Tất nhiên, tại mọi điểm trong một vũ trụ vô hạn như vậy mật độ cũng sẽ là vô hạn.
Một cách khác là hãy nghĩ Big Bang của một vũ trụ mở tựa như một đường thẳng dài vô hạn. Mặc dù nó có một số vô hạn điểm trên nó (vì một điểm có cỡ zero), nhưng rốt lại nó vẫn có thể tích zero. Khi đó chúng ta có thể tưởng tượng Vũ trụ Nhìn thấy của chúng ta lớn lên từ chỉ một điểm (một vụ nổ lớn) của đường thẳng đó. Tôi không muốn đi quá xa ở ví dụ tương tự này.
Cuối cùng, để làm cho bạn hoàn toàn bối rối, cho dù Vũ trụ bây giờ có hình dạng như thế nào, cho dù nó hầu như hoàn toàn phẳng, nhưng nó sẽ cong vô hạn tại Big Bang!
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili
Bản dịch của Thuvienvatly.com
___
6 Nếu bạn biết thêm chút ít về vũ trụ học, bạn có thể nhận thức rằng một vũ trụ có thể giãn nở mãi mãi và vẫn đóng kín. Nếu bạn là một nhà vũ trụ học, bạn không cần đọc quyển sách này làm gì.
7 Một lần nữa, điều này là không nhất thiết. Ở phần sau, tôi sẽ trình bày làm thế nào một vũ trụ mở không nhất thiết phải vô hạn về quy mô.
