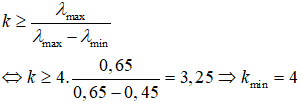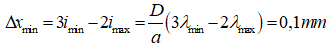Câu hỏi
🗣️ Nguyễn Thị Minh hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
Trong thí nghiệm giao thoa ánh sáng trắng bằng Y-âng, người ta dùng kính lọc sắc để chỉ cho ánh sáng từ màu lam đến màu cam đi qua hai khe (có bước sóng từ 0,45 μm đến 0,65 μm). Biết mm, khoảng cách từ hai khe đến màn D=2m. Khoảng có bề rộng nhỏ nhất mà không có vân sáng nào quan sát được trên màn bằng
(A) 0,9 mm
(B) 0,2 mm
(C) 0,5mm
(D) 0,1 mm
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: tong hop de thi thu thpt quoc gia mon vat li nam 2019.
Câu trả lời hay nhất
🕵 Bạn Hồ Trọng Bảo trả lời:
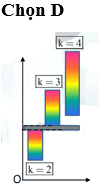
Chọn câu (D): 0,1 mm
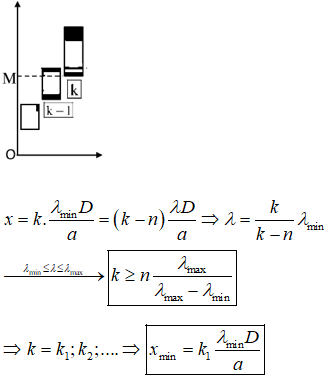
*Khoảng có bề rộng nhỏ nhất mà không có vân sáng nào quan sát được trên màn tương ứng nằm ở dưới phía liền kề khi có hai quang phổ chồng lên nhau *Bây giờ chúng ta đi xác định phổ bậc bao nhiêu thì có sự chồng lên nhau. Áp dụng công thức tính k nhanh: Do khoảng bề rộng nhỏ nhất nên có hai quang phổ chồng lên nhau suy ra n = 1 *. Như vậy ở phổ bậc bắt đầu có 3 sự trùng nhau nên dưới phổ bậc 3 là có khoảng tối nhỏ nhất. QP bậc 3 có một phần chồng với quang phổ bậc 4. Do đó QP bậc 2 và 3 không chồng lên nhau. (Quan sát hình 1). Do đó Phương pháp tổng quát. Ta lấy lấy vân sáng bậc k làm chuẩn. Từ đó chúng ta đi xác định k. Xác định được kmin tức là chúng ta đã biết được tại quang phổ bậc bao nhiêu bắt đầu có sự chồng lên nhau. Khi biết được từ quang phổ bậc bao nhiêu có sự chồng nhau thì bài toán trở nên vô cùng đơn giản. Tại một vị trí có m quang phổ chồng lên nhau tức là có m vân sáng quan sát được
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Trần Thị Đức viết:
Chọn C, 0,5mm
👤 Nguyễn Thị Dũng viết:
Chọn D, 0,1 mm
➥ 🗣️ Nguyễn Thị Minh trả lời: Cảm ơn bạn, câu này hình như có trong file doc này Tổng hợp đề thi thử thpt quốc gia môn Vật lí năm 2019
👤 Nguyễn Thị Thành viết:
Chọn B, 0,2 mm
👤 Trần Nhật Phú viết:
Chọn A, 0,9 mm
👤 Trần Thị Huy viết:
Chọn D: 0,1 mm
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Tổng hợp đề thi thử thpt quốc gia môn Vật lí năm 2019 (.doc)
- Tổng hợp đề thi thử THPT Quốc Gia môn Vật Lí năm 2020 (.doc)
- Tổng hợp 30 đề thi thử môn Vật Lí trung học phổ thông quốc gia năm 2019 (.doc)
- Tổng hợp đề thi thử thpt quốc gia môn Vật lí cực hay (.doc)
- Tổng hợp 20 đề thi thử thpt quốc gia môn Vật lí 2020 cực hay có lời giải (.doc)
- 10 đề thi thử tốt nghiệp THPT Quốc gia năm 2021 môn Vật Lí có lời giải chi tiết (Phần 2) (.doc)
- Giao thoa ánh sáng nhiều thành phần đơn sắc
- Thomas Young - người đặt nền móng cho thuyết sóng ánh sáng