Cho x1=A1cosωt+π3 (cm) và x2=A2cosωt−π4 (cm) là hai phương trình của hai dao động điều hòa cùng phương. Biết phương trình của dao động tổng hợp là x=5cosωt+φ (cm). Để

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Trần Khôi Thắng hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

(A)  $\pi /6$

(B)  $\pi /24$

(C)  $5\pi /12$

(D)  $\pi /12$

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: tong hop 20 de thi thu thpt quoc gia mon vat li 2020 cuc hay co loi giai.

Câu trả lời hay nhất

🕵 Bạn Phạm Văn Lộc trả lời:

Chọn câu (B):  $\pi /24$

Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác

Cách giải:

- Phương trình dao động của $x; x_1; x_2$: $\left\{\begin{array}{l}x=5\cos \left(\omega t+\phi \right)\\ x_1=A_1\cos \left(\omega t+\frac{\pi }{3}\right)\\ x_2=A_2\cos \left(\omega t-\frac{\pi }{4}\right)\end{array}\right.$

Suy ra:

+ Độ lệch pha giữa $x$ và $x_1$ là $\frac{\pi }{3}-\phi$

+ Độ lệch pha giữa $x$ và $x_2$ là $\phi +\frac{\pi }{4}$

+ Độ lệch pha giữa $x_1$ và $x_2$ là $\frac{\pi }{3}-\left(-\frac{\pi }{4}\right)=\frac{7\pi }{12}$

Ta có giản đồ vecto:

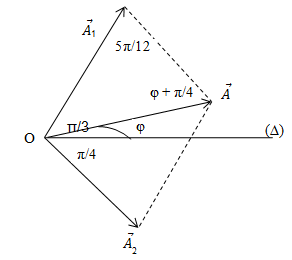
- Áp dụng định lí hàm số sin trong tam giác ta có:

$\frac{A}{\sin \frac{5\pi }{12}}=\frac{A_1}{\sin (\phi +\frac{\pi }{4})}=\frac{A_2}{\sin (\frac{\pi }{3}-\phi )}\to \left\{\begin{array}{l}{A}_1=\frac{A\sin \left(\phi +\frac{\pi }{4}\right)}{\sin \frac{5\pi }{12}}\\ A_2=\frac{A\sin \left(\frac{\pi }{3}-\phi \right)}{\sin \frac{5\pi }{12}}\end{array}\right.$

$\to A_1+A_2=\frac{A\sin \left(\phi +\frac{\pi }{4}\right)}{\sin \frac{5\pi }{12}}+\frac{A\sin \left(\frac{\pi }{3}-\phi \right)}{\sin \frac{5\pi }{12}}=\frac{A}{\sin \frac{5\pi }{12}}\left[\sin \left(\phi +\frac{\pi }{4}\right)+\sin \left(\frac{\pi }{3}-\phi \right)\right]$

- Có: $sina+sinb=2\sin \frac{a+b}{2}.c\text{os}\frac{a-b}{2}\Rightarrow \sin \left(\phi +\frac{\pi }{4}\right)+\sin \left(\frac{\pi }{3}-\phi \right)=2\sin \frac{7\pi }{24}c\text{os}\left(\phi -\frac{\pi }{24}\right)$

$\Rightarrow A_1+A_2=2A\frac{\sin \frac{7\pi }{24}}{\sin \frac{5\pi }{12}}.c\text{os}\left(\phi -\frac{\pi }{24}\right)$

Để $[A_1 + A_2]$ đạt cực đại thì: ${\left[cos\left(\phi -\frac{\pi }{24}\right)\right]}_{\text{max}}=1\Rightarrow \phi -\frac{\pi }{24}=k2\pi \Rightarrow \phi =\frac{\pi }{24}$

---

Câu trước | Câu kế tiếp

Các câu trả lời

👤 Nguyễn Anh Thành viết:

Chọn C,  $5\pi /12$

---

👤 Trần Minh Đức viết:

Chọn D,  $\pi /12$

---

👤 Đinh Văn Phú viết:

Chọn B,  $\pi /24$

➥ 🗣️ Trần Khôi Thắng trả lời: Cảm ơn bạn, câu này hình như có trong file doc này Tổng hợp 20 đề thi thử thpt quốc gia môn Vật lí 2020 cực hay có lời giải

---

👤 Dương Văn Lộc viết:

Chọn A,  $\pi /6$

---

👤 Trần Khôi Thiện viết:

Chọn B:  $\pi /24$

Gửi bạn các file hữu ích đi kèm câu hỏi:

• Tổng hợp 20 đề thi thử thpt quốc gia môn Vật lí 2020 cực hay có lời giải (.doc)
• 20 đề thi thử thpt quốc gia môn Vật lí cực hay có lời giải mới nhất (.doc)
• 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết (.doc)
• 20 Bộ đề thi thử thpt quốc gia môn Vật Lí cực hay có lời giải (.doc)
• 20 Đề luyện thi thpt quốc gia môn Vật Lí cực hay có lời giải chi tiết (.doc)
• Tổng hợp đề thi thử thpt quốc gia môn Vật lí cực hay (.doc)
• Khối Lượng và Phương Trình E = γmc2 của thế kỷ
• 7 phương trình chi phối cuộc sống của chúng ta - Phần 1