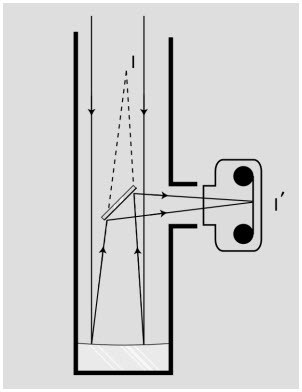
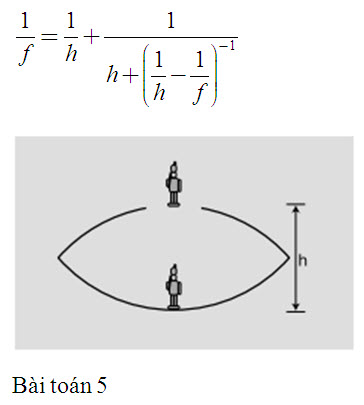
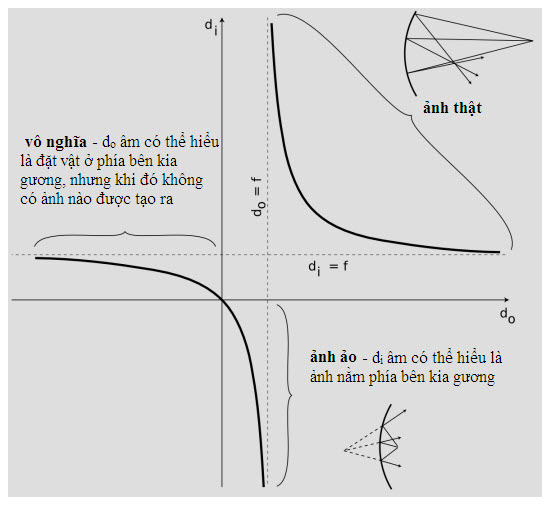
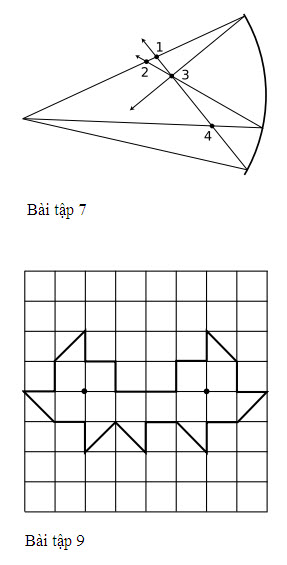
Bàn ăn Sáng, tác phẩm của Willem Clasz. de Heda, thế kỉ 17. Bức tranh thể hiện rất nhiều loại ảnh, một số ảnh bị biến dạng, do sự phản xạ và khúc xạ gây ra.
Chương 3
Khảo sát ảnh, định lượng
Nghe thì chút kì lạ khi nhà khoa học gán cho một lí thuyết là “đẹp”, nhưng đối với những người trong cuộc thì đó là một cái tên hoàn toàn ý nghĩa. Một điểm nổi bật của một lí thuyết đẹp là nó khiến chúng ta bất ngờ trước sự đơn giản của nó. Lí thuyết toán học của thấu kính và gương cầu cho chúng ta một sự bất ngờ kiểu như thế. Chúng ta nghĩ vấn đề là phức tạp vì có quá nhiều trường hợp: gương lõm thì tạo ra ảnh thật, thấu kính lõm thì tạo ra ảnh ảo, và cứ thế có tổng cộng sáu khả năng có thể xảy ra. Nếu chúng ta muốn dự đoán vị trí của ảnh trong tất cả những trường hợp này, chúng ta có thể muốn có sáu phương trình khác nhau, và thêm sáu phương trình nữa để dự đoán độ phóng đại. Thay vậy, hóa ra chúng ta có thể sử dụng chỉ một phương trình cho vị trí ảnh và một phương trình cho độ phóng đại của nó, và hai phương trình này áp dụng được cho tất cả các trường hợp mà không cần thay đổi ngoại trừ dấu cộng và dấu trừ. Đây là cái mà nhà vật lí Eugene Wigner gọi là “sự hiệu quả không lí giải nổi của toán học”. Thỉnh thoảng, chúng ta có thể tìm thấy một lí do sâu sắc hơn cho sự đơn giản bất ngờ đó, nhưng thỉnh thoảng dường như rằng Chúa đã tạo ra những bí mật của vũ trụ theo kiểu sao cho chúng có thể bị khai phá bởi một công cụ tư duy của loài người gọi là toán học.
3.1 Ảnh thật tạo bởi gương cầu lõm
Vị trí ảnh
Bây giờ chúng ta sẽ suy luận ra phương trình cho vị trí của một ảnh thật tạo bởi một gương lõm. Chúng ta sẽ giả sử cho đơn giản rằng gương có dạng cầu, nhưng thật ra đây không phải là giả thuyết bắt buộc, vì mọi cái gương lõm, đối xứng đều có thể xem là một mặt cầu. Hình dạng của cái gương có thể được xác định bằng cách cho vị trí tâm của nó, C. Một cái gương cong nhiều là một mặt cầu có bán kính nhỏ, nên C ở gần nó, còn một cái gương cong ít có C ở xa hơn. Gọi điểm O là nơi đặt vật, ta muốn tìm điểm I nơi ảnh sẽ được tạo ra.
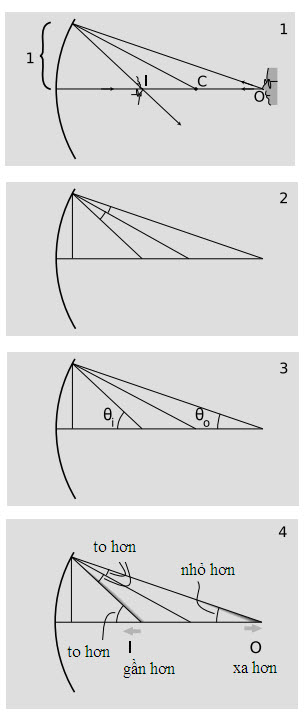
a/ Mối quan hệ giữa vị trí vật và vị trí ảnh có thể biểu diễn theo các góc qo và qi.
Để xác định ảnh, chúng ta cần lần theo ít nhất hai tia sáng phát ra từ cùng một điểm. Vì chúng ta đã chứng minh trong chương trước rằng loại ảnh này không bị biến dạng nên ta có thể sử dụng một điểm trên trục, O, trên vật, như ở hình a/1. Kết quả chúng ta suy ra cũng sẽ đúng đối với những điểm ở ngoài trục, vì nếu không ảnh sẽ bị biến dạng, cái chúng ta đã biết là không đúng. Ta cho một trong hai tia sáng phát ra theo trục chính; tia này đặc biệt dễ vẽ, vì nó phản xạ lại ngay trên trục chính. Đối với tia thứ hai, ta chọn một tia đi tới gương ở khoảng cách 1 đối với trục chính. “Một cái gì?”, độc giả sắc sảo ắt sẽ hỏi thế. Câu trả lời là một cái gì thật ra đều không thành vấn đề. Khi một cái gương cong lõm vào, toàn bộ các tia phản xạ đều đi qua cùng một điểm, nên 1 có thể biểu diễn theo bất cứ đơn vị nào mà bạn thích. Nó có thể là 1 cm chẳng hạn, trừ khi cái gương của bạn nhỏ hơn 1 cm!
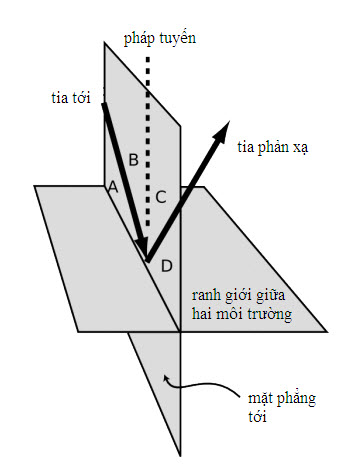
Cách duy nhất để tìm ra công thức toán học cho các tia sáng là sử dụng thực tế toán học duy nhất mà chúng ta về sự phản xạ phản chiếu: tia tới và tia phản xạ hợp những góc bằng nhau so với pháp tuyến, tia được vẽ là một đường nét mảnh. Vì thế, hai góc như thể hiện trong hình a/2 là bằng nhau, và bỏ qua một số bước chứng minh hình học đơn giản, điều này dẫn tới kết quả dễ thấy là hai góc trong hình a/3 liên hệ như sau:
θi + θo = const
(Lưu ý rằng θi và θo được đo từ ảnh và vật, chứ không phải đo từ mắt như những góc chúng ta đã nói ở mục 2.4 về số bội giác.) Ví dụ, di chuyển O ra xa gương. Góc phía trên trong hình a/2 tăng lên, nên góc phía dưới phải tăng một lượng bằng như vậy, làm cho điểm ảnh, I, di chuyển đến gần gương hơn. Theo các góc thể hiện trong hình a/3, vật càng ở xa thì góc θo càng nhỏ, và ảnh càng ở gần thì góc θi càng lớn; góc này tăng lên bao nhiêu thì góc kia giảm đi bấy nhiêu, nên tổng của chúng vẫn không đổi. Những biến đổi này được tóm tắt trong hình a/4.
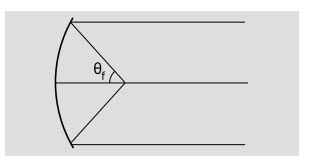
b/ Cách hiểu hình học của tiêu giác
Tổng θi + θo là một hằng số. Vậy hằng số này bằng bao nhiêu? Về mặt toán học, ta hiểu nó là hai lần góc tạo bởi đường bán kính nét mảnh. Về mặt quang học, nó là số đo sức mạnh của cái gương, tức là khả năng làm hội tụ tia sáng của cái gương, và vì thế ta gọi nó là tiêu giác, θf,
θi + θo = θf
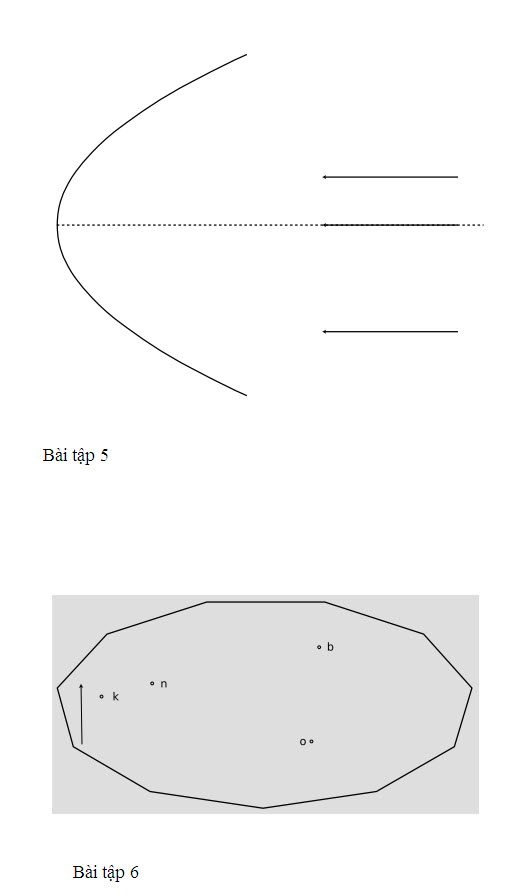
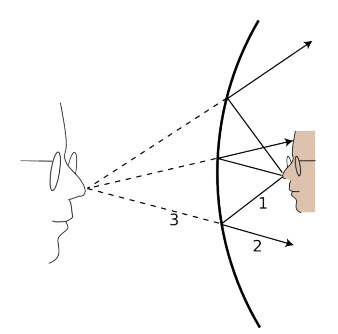
Ví dụ, giả sử chúng ta muốn sử dụng một bài kiểm tra quang nhanh và không cần chính xác để xác định một cái gương nhất định mạnh bao nhiêu. Ta có thể đặt nó lên nền nhà như thể hiện trong hình c/, và dùng nó để tạo ảnh của một ngọn đèn gắn trên trần nhà phía trên đầu mà chúng ta giả sử là ở rất xa so với bán kính cong của cái gương, sao cho cái gương chỉ nhận một nón tia sáng rất hẹp phát ra từ ngọn đèn. Cái nón này quá hẹp nên các tia sáng của nó gần như song song, và qo gần như bằng không. Ảnh thật có thể quan sát trên một tờ giấy. Bằng cách di chuyển tờ giấy đến gần hoặc ra xa, ta có thể mang ảnh vào tiêu điểm, tại đó ta biết tờ giấy đặt tại điểm ảnh. Vì θo ≈ 0, nên ta có θi ≈ θf, và khi đó ta có thể xác định tiêu giác cái gương này hoặc bằng cách đo θi trực tiếp với thước đo góc, hoặc gián tiếp qua lượng giác. Một cái gương mạnh sẽ mang các tia sáng lại với nhau để tạo ra ảnh ở gần gương, và những tia sáng này sẽ tạo ra một hình nón cụt với θi và θf lớn.
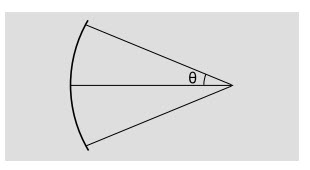
c/ Ví dụ 1, một cách kiểm tra khác để tìm tiêu giác. Cái gương giống như ở hình b.
Ví dụ 1. Một cách kiểm tra quang học khác
Hình c thể hiện một cách kiểm tra quang học khác. Thay vì đặt vật ở xa vô cùng như ở hình b, ta điều chỉnh sao cho ảnh ở ngay phía trên vật. Điểm O và I trùng nhau, và các tia sáng phản xạ sẽ chồng lên tia sáng tới. Nếu chúng ta đo góc θ như ở hình c, thì ta có thể tìm tiêu giác như thế nào?
à Góc vật và góc ảnh là bằng nhau; góc q trong hình bằng cả hai góc này. Do đó, ta có θi + θo = 2θ = θf. So sánh hình b và hình c, ta thấy hai góc gấp đôi nhau.
Tới đây, ta có thể xem như công việc của mình đã xong. Thông thường, chúng ta biết sức mạnh của gương, và ta muốn tìm vị trí ảnh đối với một vị trí vật đã cho. Cho biết tiêu giác của gương và vị trí vật, ta có thê xác định qo bằng lượng giác, làm toán trừ để tìm θi = θf – θo, và sau đó thêm vài bước rút gọn để tìm vị trí ảnh.

d/ Khoảng cách vật và khoảng cách ảnh
Tuy nhiên, có một con đường tắt có thể giúp chúng ta làm công việc này nhanh hơn nhiều. Hình a/3 thể hiện hai tam giác vuông có cạnh đáy dài bằng 1 trùng nhau, và các góc nhọn là θo và θi. Những góc này có thể liên hệ bằng lượng giác với khoảng cách vật và khoảng cách ảnh thể hiện ở hình d:
tan θo = 1/do tan θi = 1/di
Kể từ chương 2, ta đã giả sử chỉ xét những góc nhỏ. Đối với những góc nhỏ, ta có thể sử dụng sự gần đúng góc nhỏ tan x ≈ x (với x tính theo radian), nên
θo = 1/do θi = 1/di
Tương tự, ta có thể định nghĩa một khoảng cách gọi là tiêu cự, f theo θf = 1/df. Ở hình b, f là khoảng cách từ gương đến nơi các tia sáng cắt nhau. Giờ thì ta có thể biểu diễn lại phương trình liên hệ vị trí vật và vị trí ảnh như sau:
1/f = 1/di + 1/do
Hình e tóm tắt cách hiểu tiêu cự và tiêu giác1.
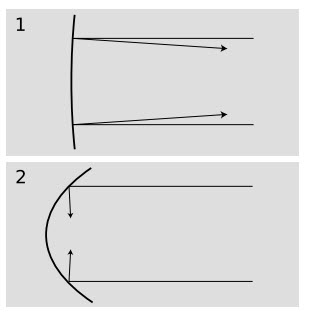
e/ Gương 1 yếu hơn gương 2. Nó có độ cong nhỏ, tiêu cự dài, và tiêu giác nhỏ hơn. Nó làm phản xạ các tia sáng ở những góc không khác nhiều so với sự phản xạ tạo ra bởi gương phẳng.
Dạng nào tốt hơn, θf = θi + θo hay 1/f = 1/di + 1/do? Dạng góc có ưu điểm là đơn giản và dễ nhìn thấy ngay, nhưng có hai lí do khiến chúng ta có thể thích dạng thứ hai hơn. Thứ nhất, giá trị số của các góc phụ thuộc vào cái ta nói là “một đơn vị” đối với khoảng cách biểu diễn là 1 trong hình a/1. Thứ hai, thường thì đo khoảng cách dễ hơn đo góc, nên dạng khoảng cách tiện lợi hơn ở chỗ tính toán. Không có dạng nào tốt hơn, vì thế chúng ta thường cần sử dụng cả hai dạng để giải một bài toán cho trước nào đó.2
Ví dụ 2. Đèn pha
Giả sử chúng ta cần tạo ra một chùm ánh sáng song song, như ở đèn pha. Một chùm sáng song song có góc giữa các tia của nó bằng không, nên θi = 0. Tuy nhiên, để đặt bóng đèn cho chúng, chúng ta cần biết một khoảng cách, chứ không phải góc: khoảng cách do giữa bóng đèn và gương. Bài toán liên quan đến cả khoảng cách lẫn góc, nên ta cần thông tin theo cả hai dạng để giải nó. Vì mục tiêu là tìm khoảng cách, nên ta hãy tìm khoảng cách ảnh tương ứng với góc đã cho θi = 0. Mà di = 1/θi nên ta có di = ∞. (Vâng, chia cho số không thì bằng vô cùng lớn. Đừng ngại vô cùng. Vô cùng là một công cụ giải toán hữu ích đấy.) Giải phương trình khoảng cách cho do ta có
do = (1/df – 1/di)-1
= (1/f – 0)-1
= f
Bóng đèn phải đặt cách gương một khoảng bằng tiêu cự của nó.
Ví dụ 3. Diopter
Một phương trình như di = 1/θi thật ra chẳng có ý nghĩa khi xét theo đơn vị. Các góc không có đơn vị, vì radian thật sự chẳng phải là đơn vị, nên vế phải phương trình là không có đơn vị. Ta không thể có vế trái có đơn vị của khoảng cách nếu như vế phải của phương trình không có đơn vị. Đây là sản phẩm của phát biểu phóng túng của tôi rằng chùm tia hình nón tỏa ra cách trục chính nơi chúng đi tới gương một khoảng cách bằng 1 mà không nói đo 1 này theo đơn vị gì. Trong cuộc sống thực tế, những người đo thị lực định nghĩa cái chúng ta gọi là θi = 1/di là “độ tụ” của một thấu kính hay gương, và đo nó theo đơn vị mét nghịch đảo (m-1), còn gọi là diopter (1 D = 1 m-1).
Độ phóng đại
Chúng ta đã thảo luận trong chương trước làm thế nào tìm độ phóng đại của một ảnh ảo tạo bởi một gương cầu. Kết quả là giống như với ảnh thật, và chúng ta thừa nhận phần chứng minh đó. Theo kí hiệu mới của chúng ta, kết quả là M = di/do. Một ví dụ số được trình bày trong mục 3.2.
______________
1Một cuộc thảo luận trực tuyến mới đây giữa một số giáo viên dạy vật lí (https://carnot.physics.bualo.edu/archives, tháng 2/2006) cho thấy nhiều người không thích thuật ngữ trên, cảm thấy nó sai lạc, hoặc không biết nó và sẽ phớt lờ nếu như gặp nó. Nghĩa là, nó dường như là cái mà các nhà ngữ pháp học gọi là “thuật ngữ dỏm” – một từ khiến một nửa dân số bực mình khi nó bị sử dụng sai và khiến nửa dân số còn lại bực mình khi nó được sử dụng đúng.
2Tôi muốn cảm ơn Fouad Ajami cho việc trình bày những ưu điểm sư phạm của việc sử dụng hai phương trình đồng thời.
Quang học
Benjamin Crowell
Bản dịch của Thuvienvatly.com
Phần tiếp theo >>