3.2 Những trường hợp khác với gương cầu
Phương trình di = có thể dễ dàng mang lại một kết quả âm, nhưng chúng ta đã nghĩ di là khoảng cách, và khoảng cách thì không thể âm. Một vấn đề tương tự xảy ra θi = θf – θo với θo > θf. Vậy tiếp theo nên xử lí thế nào?
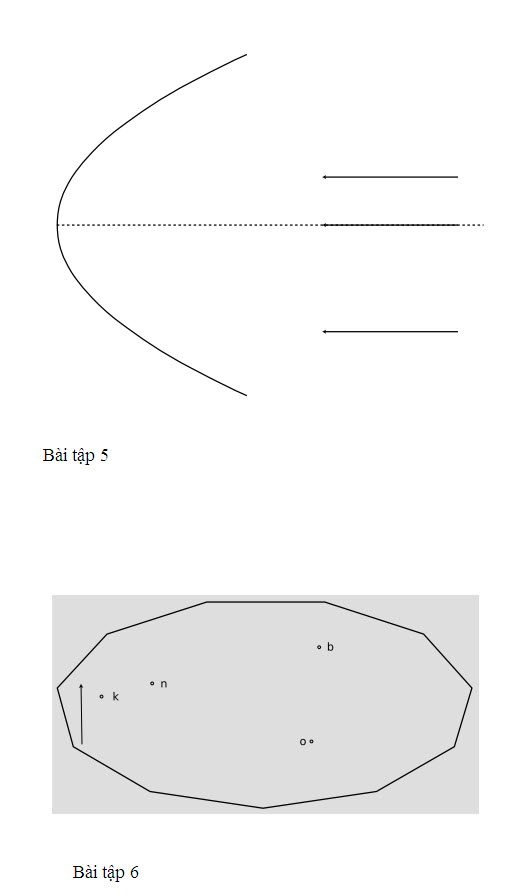
Cách lí giải phương trình góc là dễ hiểu nhất. Khi chúng ta mang vật càng đến gần ảnh, thì qo càng lớn dần, và cuối cùng ta đạt tới điểm tại đó θo = θf và θi = 0. Góc vật lớn này thể hiện một bó tia sáng tạo thành một hình nón rất rộng, rộng đến mức cái gương không còn có thể bẻ cong chúng để chúng hội tụ trở lại trên trục chính nữa. Góc ảnh θi = 0 thể hiện một bó tia sáng đi ra song song nhau. Các tia đi ra không bao giờ cắt nhau, nên đây không phải là ảnh thật, trừ khi chúng ta muốn độ lượng và nói rằng các tia cắt nhau ở vô cùng. Nếu ta tiếp tục mang vật đến gần hơn nữa, ta sẽ thu được ảnh ảo.
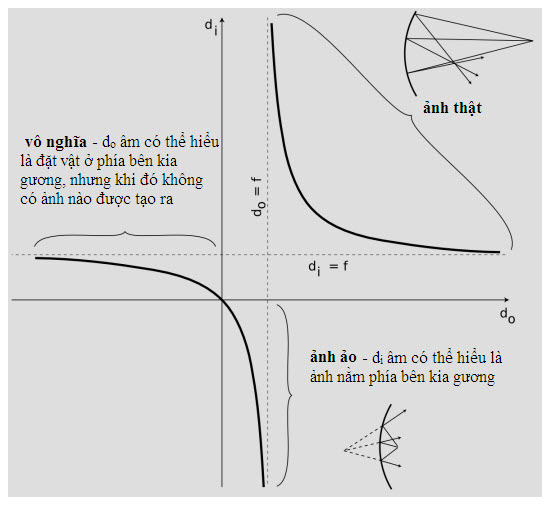
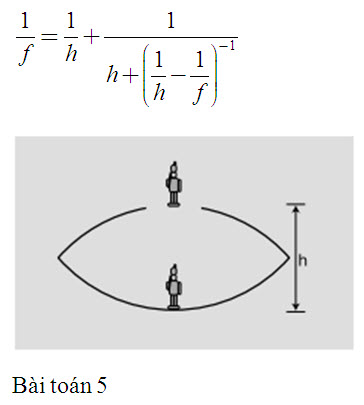
f/ Đồ thị của khoảng cách ảnh di là hàm của khoảng cách vật do.
Để phân tích phương trình khoảng cách, hãy nhìn vào đồ thị của di là hàm của do. Nhánh ở phía trên bên phải tương ứng với trường hợp ảnh thật. Nói đại khái, đây chỉ là phần đồ thị chúng ta đã chứng minh tương ứng với thực tế, vì chúng ta chưa làm phân tích hình học nào cho những trường hợp khác, ví dụ như các ảnh ảo. Như đã trình bày trong phần trước, cho do càng lớn thì làm cho di càng nhỏ, và ngược lại.
Cho do nhỏ hơn f là tương đương với θo > θf: một ảnh ảo được tạo ra ở phía bên kia của gương. Đây là thí dụ đầu tiên của “sự hiệu quả không thể lí giải nổi của toán học” của Wigner mà chúng ta từng gặp trong quang học. Mặc dù chứng minh của chúng ta phụ thuộc vào giả thuyết rằng ảnh là thật, nhưng phương trình chúng ta suy luận ra hóa ra có thể áp dụng cho ảnh ảo, miễn là chúng ta hiểu những dấu âm và dương theo một kiểu nhất định, hoặc là biến đổi phương trình để có những dấu âm và dương khác nhau.
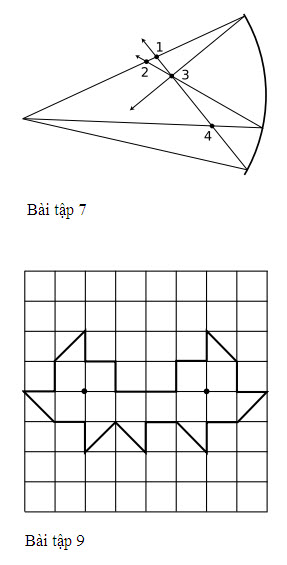
Tự kiểm tra A
Hãy giải thích ba chỗ nơi đồ thị đi tới một trong những đường đứt nét trong phần đồ thị thực tế vật lí ở trên. [Yêu cầu sẽ xuất hiện tự nhiên hơn nếu bạn đã học khái niệm giới hạn trong toán học.]
Ví dụ 4. Gương phẳng
Chúng ta còn có thể áp dụng phương trình cho gương phẳng. Khi mặt cầu to dần ra thì bề mặt của nó cong nhẹ nhàng hơn. Chẳng hạn, hành tinh Trái đất quá lớn nên chúng ta thậm chí không hề cảm nhận thấy độ cong của bề mặt của nó. Để biểu diễn một cái gương phẳng, chúng ta đặt bán kính cong của gương, và tiêu cự của nó, trở nên vô hạn. Chia cho vô hạn thì bằng không nên ta có
1/do = – 1/di
hoặc
do = – di
Nếu chúng ta hiểu dấu trừ là biểu thị một ảnh ảo nằm ở phía sau gương thì phương trình trên có nghĩa.
Hóa ra đối với bất kì kết hợp nào trong sáu kết hợp có thể có của ảnh thật và ảnh ảo tạo bởi thấu kính hoặc gương lồi và lõm, ta có thể áp dụng những phương trình có dạng
θf = θi + θo
và
1/f = 1/di + 1/do
chỉ với một biến đổi của các dấu cộng và trừ. Có hai cách tiếp cận có thể có ở đây. Phương pháp chúng ta vừa sử dụng là phương pháp phổ biến hơn trong sách vở của Mĩ: giữ phương trình không đổi, nhưng thêm sự giải thích cho các giá trị âm và dương thu được của các biến. Vấn đề đối với phương pháp này là khi đó người ta phải học thuộc các bảng đổi dấu, ví dụ như giá trị của di là âm khi ảnh là ảnh ảo tạo bởi một gương lõm. Rồi phải học thuộc các dấu âm và dương cho tiêu cự nữa. Ôi! Hiếm có cô cậu học trò nào nhớ nổi những cái bảng dài ngoằn này trong đầu trong hơn năm phút sau khi bước ra khỏi phòng thi hết môn vật lí. Tất nhiên, người ta có thể luôn luôn tìm kiếm các thứ khi cần đến, nhưng kết quả là biến vấn đề thành một bài tập thay số vào công thức một cách mù quáng mất rồi.
Như bạn đã thu nhặt cho đến đây, có một phương pháp khác tôi nghĩ là tốt hơn, và tôi sẽ sử dụng trong suốt phần còn lại của quyển sách này. Trong phương pháp này, toàn bộ các khoảng cách và góc là dương theo định nghĩa, và chúng ta đưa các dấu cộng và trừ vào phương trình tùy thuộc vào tình huống. (Tôi nghĩ tôi là người đầu tiên phát minh ra phương pháp này, nhưng tôi còn nghe nói đây là cách đổi dấu kiểu châu Âu và nó khá phổ biến ở châu Âu.) Thay vì học thuộc những dấu này, chúng ta bắt đầu với những phương trình khái quát
θf = ±θi ± θo
1/f = ±1/di ± 1/do
và sau đó xác định dấu bằng một phương pháp hai bước tùy thuộc vào sơ đồ tia sáng. Thật ra chỉ có hai dấu để mà xác định, chứ không phải bốn; dấu trong hai phương trình phải khớp với cái bạn trông đợi. Phương pháp là như sau:
1. Sử dụng sơ đồ tia sáng xác định xem qo và qi biến thiên theo kiểu giống nhau hay ngược nhau. (Nói cách khác, xác định xem cho qo lớn hơn thì giá trị của qi lớn hơn hay nhỏ hơn.) Dựa trên điều này, xác định xem hai dấu trong phương trình góc là cùng dấu hay trái dấu. Nếu dấu là giống nhau, thì chuyển sang bước 2 để xác định xem là dương hay âm.
2. Nếu hai dấu ngược nhau thì ta phải biết dấu nào là dương, dấu nào là âm. Vì tiêu giác không bao giờ âm, nên góc nhỏ hơn phải là góc có dấu trừ.
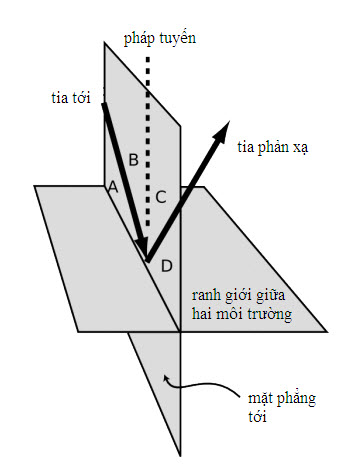
Trong bước 1, nhiều học sinh gặp khó khăn với việc vẽ sơ đồ tia sáng thật chính xác. Để đơn giản, bạn nên luôn luôn vẽ sơ đồ cho một điểm ở trên vật trên trục của gương và để cho một trong các tia sáng là tia phát dọc theo trục chính và phản xạ lại chính nó, như những hình vẽ ở mục 3.1. Như thể hiện trong hình a/4 ở mục 3.1, có bốn góc có liên quan: hai góc tại gương, một góc tại vật (θo) và một góc tại ảnh (θi). Hãy đảm bảo vẽ pháp tuyến với gương để bạn có thể nhìn thấy hai góc tại gương. Hai góc này bằng nhau, cho nên khi bạn thay đổi vị trí vật, bạn làm nó xòe ra hoặc khép lại, giống như mở hoặc đóng một quyển sách vậy. Một khi bạn đã vẽ xong hiệu ứng này, bạn sẽ có thể dễ dàng nói θo và qi thay đổi cùng chiều hay ngược chiều.
Mặc dù tiêu cự luôn luôn là dương trong phương pháp dùng trong quyển sách này, nhưng bạn nên nhận thức rằng gương và thấu kính lồi được gán cho tiêu cự âm trong phương pháp kia, nên nếu bạn nhìn thấy một thấu kính ghi f = - 30 cm thì bạn sẽ biết nó có nghĩa là gì.
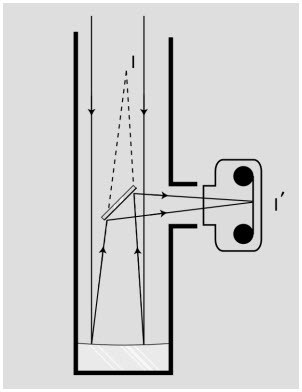
Ví dụ 5. Gương chống trộm
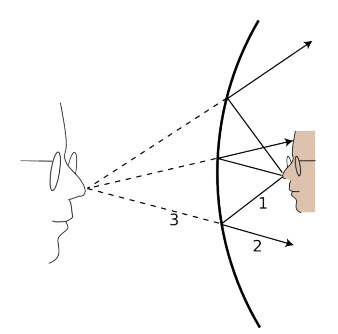
Các cửa hàng tiện lợi thường lắp đặt một cái gương lồi để người bán hàng có thể quan sát toàn bộ cửa hàng và có thể bắt trộm. Hãy sử dụng sơ đồ tia sáng chứng minh rằng ảnh bị thu nhỏ, mang lại tầm nhìn rộng hơn cho người bán hàng. Nếu tiêu cự của gương là 3,0 m, và gương đặt cách bức tường xa nhất là 7,0 m, thì ảnh của cửa hàng ở sâu bao nhiêu?

g/ Ví dụ 5
Như thể hiện trong sơ đồ tia sáng g/1, di nhỏ hơn do. Độ phóng đại, M = di/do, sẽ nhỏ hơn một, tức là ảnh thật sự bị thu nhỏ chứ không phóng to.
Áp dụng phương pháp vừa nêu ở trên để xác định các dấu cộng và trừ. Bước 1: Vật là điểm nằm trên bức tường đối diện. Như một thí nghiệm, g/2, di chuyển vật đến gần hơn. Tôi vẽ những hình này bằng một phần mềm vi tính, nhưng nếu bạn vẽ bằng tay, bạn nên chọn tỉ lệ lớn hơn để có độ chính xác hơn. Đồng thời, mặc dù tôi tách hình g thành hai hình độc lập để làm cho dễ hiểu hơn, nhưng bạn sẽ ít phạm sai lầm hơn nếu bạn vẽ chúng chồng lên nhau.
Hai góc tại gương xòe ra từ pháp tuyến. Tăng qo rõ ràng cũng làm cho qi tăng lên. (Cả bốn góc đều lớn lên.) Phải có một sự triệt tiêu các ảnh hưởng của việc thay đổi hai số hạng ở vế phải theo kiểu giống nhau, và cách duy nhất để có một sự triệt tiêu như vậy là nếu hai số hạng trong phương trình góc có dấu ngược nhau:
θf = +θi – θo
hay
θf = –θi + θo
Bước 2. Giờ thì số hạng nào dương, số hạng nào âm? Vì góc ảnh lớn hơn góc vật, nên phương trình góc phải là
θf = θi – θo
để mang lại kết quả dương cho tiêu giác. Dấu của phương trình khoảng cách hành xử giống như vậy:
1/f = 1/di - 1/do
Giải cho di, ta được
di = (1/f + 1/do)-1 = 2,1 m
Ảnh của cửa hàng bị thu nhỏ theo tỉ lệ 2,1/7,0 = 0,3, tức là nó nhỏ đi 70%.
Ví dụ 6. Đường đi tắt cho ảnh thật
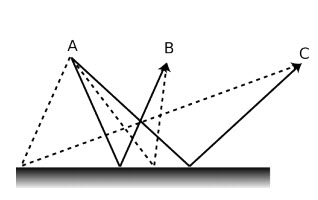
Trong trường hợp ảnh thật, có một đường đi tắt cho bước 1, xác định dấu. Ở ảnh thật, các tia sáng cắt nhau tại vật lẫn tại ảnh. Vì thế, ta có thể đổi chiều thời gian sơ đồ tia sáng, sao cho toàn bộ tia sáng đang đi ra từ ảnh và hội tụ trở lại tại vật. Vật và ảnh có vai trò hoán đổi. Do sự đối xứng đảo chiều thời gian này, cho nên vật và ảnh không thể xử lí khác nhau trong mọi phương trình, và do đó chúng phải có cùng dấu. Chúng đều là dương, vì chúng phải cộng lại cho một kết quả dương.
Quang học
Benjamin Crowell
Bản dịch của Thuvienvatly.com
Phần tiếp theo >>