ACHILLES VÀ CON RÙA
“Mọi chuyển động đều là ảo giác.”
Xếp thứ nhất trong chín nghịch lí của chúng ta có từ hai thiên niên kỉ rưỡi về trước, đã lâu như thế rồi nên chúng ta phải hâm nóng nó lại, hẳn bạn sẽ không thấy bất ngờ khi nghe nói rằng nó đã được người ta hiểu và giải thích thấu đáo. Thế nhưng đa số mọi người lần đầu gặp phải nó đều vò đầu bứt tai suy nghĩ. Nó được gọi là Nghịch lí Achilles (hay Vấn đề Achilles và Con rùa) và nó chỉ là một trong một loạt vấn đề được nêu ra bởi nhà triết học Hi Lạp Zeno vào thế kỉ thứ năm trước Công nguyên. Là một ví dụ về logic thuần túy, nó chẳng thể đơn giản hơn được nữa. Thế nhưng đừng để bị lừa; trong chương này chúng ta sẽ xét một vài nghịch lí của Zeno và làm sáng tỏ bằng cách mang những ý tưởng của ông về thời đại ngày nay với một phiên bản chỉ có thể giải thích bằng thuyết lượng tử. Vâng, tôi chưa hề nói chuyện sẽ diễn ra dễ dàng cho bạn nhé.
Ta hãy bắt đầu với nghịch lí nổi tiếng nhất của Zeno. Một con rùa được chấp cho xuất phát trước trong một cuộc chạy đua với Achilles thần tốc sao cho nó bò đến một điểm nào đó (hãy gọi đó là điểm A) trên đường đua vào lúc Achilles xuất phát. Vì Achilles chạy nhanh hơn con rùa bò rất nhiều, nên chàng sẽ sớm đi tới điểm A. Tuy nhiên, lúc chàng đi tới A thì còn rùa đã bò thêm một đoạn ngắn tới một điểm xa hơn, ta sẽ gọi đó là điểm B. Khi Achilles đi tới điểm B, con rùa đã bò tới điểm C, và cứ thế. Vì thế, trong khi rõ ràng Achilles đuổi kịp con rùa, và khoảng cách giữa họ sau mỗi giai đoạn càng nhỏ hơn một chút, nhưng có vẻ như chàng sẽ không bao giờ thật sự đuổi kịp nó. Vậy chúng ta sai ở đâu?
Khi nói đến sự thông minh, làm chủ những câu hỏi logic hóc búa và động não, hay chỉ tư duy sâu sắc nói chung, bạn không thể bì kịp người Hi Lạp cổ đại. Thật vậy, những nhà triết học cổ xưa này rất sâu sắc, logic của họ rất thông thái, đến mức chúng ta có xu hướng quên mất họ đã sống hơn hai nghìn năm về trước. Thậm chí ngày nay, khi chúng ta muốn nêu ví dụ về thiên tài, cùng với Einstein lừng danh, chúng ta thường viện dẫn những tên tuổi như Socrates, Plato, và Aristotle làm đại diện cho những trí tuệ lỗi lạc nhất.
Zeno chào đời ở Elea, một đô thành Hi Lạp xưa, ngày nay thuộc miền tây nam Italy. Cuộc đời và sự nghiệp của ông ít được biết tới, ngoài việc ông là học trò của một nhà triết học Elea khác, Parmenides. Cùng với một nhân vật thứ ba sống trong cùng đô thành Elea, Melissus, họ lập thành cái ngày nay gọi là phong trào Elea. Triết học của họ nói rằng bạn không nên lúc nào cũng tin tưởng vào các giác quan của mình và dùng trải nghiệm để nhận thức thế giới, mà rốt lại nên dựa vào logic và toán học. Nói chung, đây là một cách tiếp cận hợp lí; thế nhưng, như chúng ta sẽ sớm thấy, chính nó đã dẫn Zeno đi sai đường.
Từ những gì ít ỏi mà chúng ta biết về những ý tưởng của Zeno, có vẻ như Zeno không có nhiều quan điểm tích cực của riêng ông, mà thay vậy ông hay đả phá lập luận của người khác. Dẫu vậy, chính Aristotle, người sống sau Zeno một thế kỉ, xem ông là người sáng lập của một kiểu tranh luận gọi là “biện chứng”. Đây là một hình thức tranh luận khai hóa mà người Hi Lạp xưa – đặc biệt như Plato và Aristotle – rất nổi trội, sử dụng logic và lý tính để giải quyết các bất đồng.
Chỉ một đoạn ngắn công trình gốc của Zeno còn sót lại đến ngày nay, vì thế những gì chúng ta biết về ông là đến từ trước tác của những người khác, nổi bật là Plato và Aristotle. Khoảng năm bốn mươi tuổi, Zeno đến Athens, tại đó ông gặp chàng trai trẻ Socrates. Về cuối đời, ông tham gia tích cực vào tình hình chính trị Hi Lạp, và cuối cùng bị bỏ tù và bị tra tấn đến chết vì tham gia trong một âm mưu chống lại nhà cầm quyền địa phương ở Elea. Một câu chuyện kể về ông nói rằng ông không chịu khai báo và còn nhổ nước bọt vào những kẻ bắt giữ ông chứ không phản bội đồng chí của mình. Thế nhưng ông được biết tới nhiều nhất qua một loạt nghịch lí được Aristotle mang đến với chúng ta trong tác phẩm vĩ đại của ông, Vật lí học. Người ta tin rằng có khoảng bốn mươi nghịch lí cả thảy, nhưng chỉ một ít còn sót lại mà thôi.
Toàn bộ những nghịch lí của Zeno – bốn nghịch lí nổi tiếng nhất được Aristotle đặt tên là: Achilles, Lưỡng phân, Đường đua, và Mũi tên – đều tập trung vào ý tưởng nói rằng chẳng có gì từng thay đổi hết; rằng chuyển động chỉ là một ảo giác và bản thân thời gian không thật sự tồn tại. Tất nhiên, nếu có một thứ mà người Hi Lạp nổi trội thì đó là sự triết lí, và những nhận định vĩ đại kiểu như “mọi chuyển động đều là ảo giác” chỉ là một sự trừu tượng mang tính khiêu khích mà họ vốn nổi tiếng. Ngày nay, chúng ta có thể đả phá những nghịch này bằng khoa học; song chúng thú vị lắm nên đáng để chúng ta xem xét lại ở đây. Trong chương này, tôi sẽ lần lượt xem xét chúng và chỉ ra mỗi nghịch lí có thể được giải quyết như thế nào với một chút phân tích khoa học thận trọng. Hãy bắt đầu với nghịch lí mà tôi đã nêu ở tiêu đề chương này.
ACHILLES VÀ CON RÙA
Đây là nghịch lí Zeno mà tôi yêu thích, bởi lẽ thoạt nhìn nó hoàn toàn logic, thế nhưng thật ra nó phủ nhận logic bằng một cách bất ngờ. Achilles là chiến binh vĩ đại nhất trong thần thoại Hi Lạp, được trời ban sức mạnh, lòng gan dạ, và kĩ năng quân sự tuyệt vời. Nửa người, nửa siêu nhiên – bố mẹ chàng là Vua Peleus xứ Thessaly và nữ thần biển cả tên gọi là Thetis – chàng là nhân vật sáng giá trong Iliad của Homer, tác phẩm kể về Cuộc chiến thành Trojan. Truyện kể rằng lúc còn là cậu nhóc, chàng đã có thể chạy đủ nhanh để đuổi kịp một con hươu và đủ khỏe để giết chết một con sư tử. Vì thế rõ là Zeno muốn nhấn mạnh sự đối lập khi ông chọn người anh hùng thần thoại này chạy đua với con rùa chậm chạp.
Nghịch lí được xây dựng trên một câu truyện ngụ ngôn còn xưa hơn nữa về thỏ và rùa, tác giả của nó được cho là một người Hi Lạp cổ đại khác, tên là Aesop, sống trước Zeno một thế kỉ. Trong truyện ngụ ngôn gốc, rùa bị thỏ chế giễu nên thách thỏ chạy đua, cuối cùng thì rùa thắng vì thỏ nhởn nhơ nghĩ rằng nó thể dừng lại nô đùa ở giữa đường, chỉ đến khi sực nhớ thì đã quá muộn để đuổi kịp rùa.
Trong phiên bản của Zeno, chàng Achilles nhanh chân giữ vai trò của thỏ. Không giống thỏ, chàng hoàn toàn tập trung vào nhiệm vụ; nhưng chàng chấp rùa xuất phát trước, và điều này có vẻ làm hỏng thanh danh của chàng, vì rùa có vẻ luôn giành phần thắng cuộc đua, cho dù đường đua dài bao nhiêu, cho dù ngày xưa có máy chụp ảnh đi chăng nữa. Theo lập luận của Zeno, cho dù người anh hùng chạy nhanh bao nhiêu, và cho dù đối thủ của chàng bò chậm bao nhiêu, Achilles sẽ không bao giờ đuổi kịp con rùa. Chắc chắn đây không phải là cái xảy ra trên thực tế chứ?
Đây là một câu đố nghiêm túc đối với các nhà toán học Hi Lạp, họ chưa có khái niệm thực tế về cái chúng ta gọi là một chuỗi vô hạn hội tụ, hay quả vậy họ chưa có quan niệm về chính cái vô hạn (những ý tưởng sẽ được tôi giải thích ngắn gọn cho bạn trong chốc lát). Aristotle chắc chắn không phải là kẻ vụng về khi nghĩ về những vấn đề như thế, ông xem các nghịch lí Zeno là “ngụy biện”. Vấn đề là ở chỗ không có ai trong số Aristotle hay bất kì người nào khác ở Hi Lạp xưa hiểu đúng về một trong những công thức đại số căn bản nhất trong vật lí học: tốc độ bằng quãng đường chia cho thời gian. Ngày nay chúng ta có thể làm tốt hơn nhiều.
Mệnh đề “sẽ không bao giờ đuổi kịp con rùa” tất nhiên là sai, vì những khoảng cách giảm dần đang được xem xét theo từng giai đoạn (giữa điểm A và B, và giữa B và C, và vân vân), cũng liên quan đến những khoảng thời gian giảm dần, và vì thế cho dù một số vô hạn giai đoạn không hàm nghĩa là một độ dài thời gian vô hạn. Thật vậy, các giai đoạn cộng lại toàn bộ cho một thời gian hữu hạn: thời gian cần thiết cho Achilles đuổi kịp con rùa! Thứ nhập nhằng ở nghịch lí trên là đa số mọi người không hiểu đúng việc cộng một chuỗi số vô hạn không nhất thiết dẫn tới một kết quả vô hạn. Mặc dù nghe có vẻ lạ, nhưng một số vô hạn giai đoạn có thể được hoàn chỉnh trong một thời gian hữu hạn, và còn rùa sẽ bị đuổi kịp và qua mặt dễ dàng, như logic nhấn mạnh. Lời giải dựa trên cái được các nhà toán học gọi là chuỗi hình học.
Xét ví dụ sau:
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ...
Rõ ràng bạn có thể tiếp tục cộng thêm những phân số nhỏ dần nhỏ mãi, cho tổng càng lúc càng tiến gần giá trị 2. Hãy thử bằng cách vẽ một đoạn thẳng rồi chia nó làm hai phần, sau đó chia đoạn bên phải làm hai phần, và tiếp tục làm thế cho đến khi các phần chia quá nhỏ khiến bạn không còn đánh dấu nó trên trang giấy được nữa. Giả sử nửa đoạn thẳng ban đầu là một đơn vị độ dài (cho dù là centi mét, inch, mét hay dặm là không thành vấn đề), thì bằng cách cộng gộp các phân số liên tiếp, như trong chuỗi được viết ở trên, chúng hội tụ về độ dài tổng bằng hai đơn vị.
Hình 2.1 Một chuỗi vô hạn hội tụ
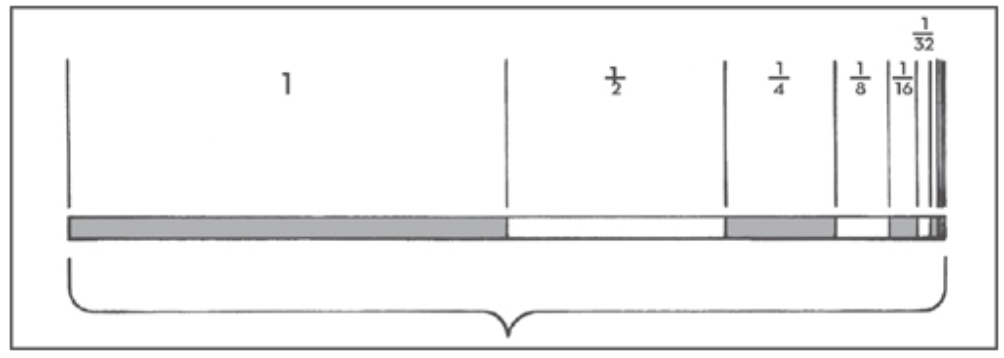
Lấy tổng một số vô hạn độ dài giảm dần – cộng các độ dài giảm mãi không có nghĩa là đáp số cuối cùng là vô hạn vì các độ dài càng lúc càng nhỏ lại.
Một cách hay để áp dụng phép lấy tổng này cho nghịch lí trên là xét không phải điểm tương ứng tại đó Achilles và con rùa đi tới ở mỗi giai đoạn, mà xét khoảng cách giảm dần giữa họ. Vì họ đều đang chuyển động ở một tốc độ không đổi, nên khoảng cách này cũng đang giảm dần ở một tốc độ không đổi. Ví dụ, giả sử Achilles chấp con rùa bò trước 100 mét rồi sau đó bắt đầu đuổi theo nó ở tốc độ 10 mét trên giây, thì kết quả là như thế nào theo Zeno? Vâng, khoảng cách giữa họ được chia đôi sau năm giây. Khoảng cách còn lại được chia đôi sau hai giây rưỡi, rồi khoảng cách còn lại tiếp theo được chia đôi sau một và một phần tư giây, và cứ thế. Nếu muốn, chúng ta có thể tiếp tục cộng những khoảng cách nhỏ dần đi được trong những khoảng thời gian giảm dần này, nhưng thực tế là nếu Achilles đuổi theo con rùa ở tốc độ 10 mét trên giây thì chàng sẽ bắt kịp nó trong 10 giây, đó là thời gian chàng cần để khép kín khoảng cách ban đầu 100 mét về zero. Và giá trị 10 giây này đúng là con số chúng ta thu được nếu chúng ta cộng 5 giây + 2,5 giây + 1,25 giây + 0,625 giây… và cứ thế cho đến khi con số cộng tiếp theo quá nhỏ và chúng ta rãnh rỗi dành cả ngày để đọc đáp số (9,9999… giây). Sau 10 giây, tất nhiên Achilles sẽ vượt và dẫn trước con rùa đúng như trông đợi (trừ khi chàng quyết định dừng lại dọc đường thưởng thức bia bọt – không phải thứ Zeno cảm thấy cần thiết để làm sáng tỏ lập luận của ông).
LƯỠNG PHÂN
Nghịch lí tiếp theo của Zeno bác bỏ thực tế về chuyển động và là một biến thể cùng chủ đề với Nghịch lí Achilles. Nó phát biểu rất đơn giản:
Để đi tới đích, trước tiên bạn phải đi hết một nửa quãng đường, nhưng để đi hết một nửa quãng đường đó trước tiên bạn đi hết một phần tư quãng đường, và để đi hết một phần tư quãng đường đó bạn phải đi hết một phần tám quãng đường, và cứ thế. Nếu bạn có thể tiếp tục chia đôi quãng đường mãi mãi, thì bạn không bao giờ đi hết quãng đường đã đánh dấu, và vì thế bạn không bao giờ thật sự bắt đầu chuyến đi của mình. Ngoài ra, chuỗi quãng đường ngắn gần như không hồi kết này là vô hạn. Vì thế để hoàn tất chuyến đi đòi hỏi bạn hoàn tất một số vô hạn nhiệm vụ. Vì thế bạn không bao giờ có thể hoàn thành nó. Nếu bạn không thể bắt đầu chuyến đi và sẽ không bao giờ hoàn thành nó, thì bản thân chuyển động là không thể.
Chúng ta học được nghịch lí này từ Aristotle, ông biết rằng nó phi lí nhưng vẫn tìm kiếm lập luận logic để có thể bác bỏ nó một cách thuyết phục. Xét cho cùng, một thứ đại loại như chuyển động là điều hiển nhiên. Tuy nhiên, Zeno đang áp dụng một hình thức tranh luận gọi là reductio ad absurdum, đó là quy kết một ý tưởng là vô lí bằng cách chứng minh rằng nó sẽ dẫn tới một kết luận phi lí không tránh khỏi. Ta cũng nên nhớ rằng Zeno không phải nhà toán học. Ông đang tranh biện chỉ viện dẫn logic thuần túy, và thường như thế là không đủ. Các triết gia Hi Lạp khác thường dùng đến một cách tiếp cận trực tiếp và thực dụng hơn nhằm bác bỏ những lập luận của Zeno về ảo giác chuyển động. Một trong số họ là Diogenes Kẻ yếm thế.
Từ “chủ nghĩa yếm thế” của chúng ta có xuất xứ từ một phong trào triết học duy tâm của người Hi Lạp xưa. Phe yếm thế Hi Lạp là một nhóm người có nghĩa cử cao đẹp hơn nghĩa rộng hiện đại của tên gọi của họ nói lên: họ từ chối sự giàu có, quyền lực, danh vọng, cả sự sở hữu, và thay vậy chọn lấy một cuộc sống giản đơn không có mọi dục vọng vốn có của con người. Họ tin rằng mọi chúng sinh đều bình đẳng và thế giới được chia đều cho mỗi người. Có lẽ nổi tiếng trong nhóm Yếm thế là Diogenes, sống cùng thời với Plato vào thế kỉ thứ tư trước Công nguyên. Nhà triết học này là tác giả của một số câu trích dẫn tuyệt vời nhất mà bạn sẽ tìm thấy, ví dụ như “Hồng má là màu của tiết hạnh”, “Chó và triết gia làm việc tốt nhất và được thưởng ít nhất”, “Kẻ ít hài lòng nhất là kẻ có nhiều nhất”, và “Tôi chẳng biết gì, ngoại trừ thực tế là tôi ngu dốt”.
Diogenes đưa các giáo điều của chủ nghĩa Yếm thế đến cực độ logic của chúng. Hình như ông muốn tỏ đức hạnh nghèo khó và ông đã sống mấy năm trong một khu cống rãnh trong một khu chợ Athens. Ông nổi tiếng là nhạo báng tất tần tật mọi thứ, đặc biệt là nhiều giáo điều triết lí của thời ấy, kể cả của những người nổi tiếng như Socrates và Plato. Vì thế bạn có thể hình dung những gì ông nghĩ về Zeno và những nghịch lí của ông ta. Lúc nghe nói tới Nghịch lí Lưỡng phân của Zeno về ảo giác chuyển động, ông chỉ việc đứng lên và bước đi, chứng minh rành rành sự phi lí của những kết luận của Zeno.
Trong khi chúng ta có thể hoan nghênh Diogenes vì cách tiếp cận thực tế của ông, ta vẫn nên nghiên cứu tỉ mỉ hơn một chút xem logic của Zeno sụp đổ ở đâu. Và hóa ra thì chẳng khó khăn gì – xét cho cùng, chúng ta có hơn hai nghìn năm để làm sáng tỏ. Dẫu sao, mặc dù bạn có thể cảm thấy chỉ cần lẽ thường tình là đủ để bác bỏ nghịch lí của Zeno, nhưng tôi thì không thế. Tôi đã dành phần lớn cuộc đời mình làm việc và, quan trọng hơn, suy nghĩ với tư cách một nhà vật lí, và tôi không hài lòng với những lập luận mang tính chung chung, triết lí, hay logic nhằm bác bỏ Nghịch lí Lưỡng phân. Tôi cần vật lí học chặt chẽ – đối với tôi, nó làm công việc thuyết phục tốt hơn nhiều.
Cái chúng ta cần làm là biến đổi lập luận của Zeno về quãng đường thành lập luận về thời gian. Giả sử bạn đang chuyển động ở một tốc độ không đổi tại thời điểm bạn đứng tại điểm xuất phát của chuyến đi. Khái niệm về tốc độ, mà Zeno không hiểu rõ lắm, có nghĩa là đi hết một quãng đường nhất định trong một thời gian hữu hạn. Quãng đường bạn phải đi càng ngắn, thì thời gian cần thiết để đi hết nó càng ngắn, nhưng hễ khi bạn chia số thứ nhất cho số thứ hai chúng luôn cho đáp số giống nhau: đó chính là tốc độ của bạn. Bằng cách xét những quãng đường càng lúc càng ngắn phải đi hết trước khi bạn bắt đầu chuyến đi của mình, bạn cũng đang xét những khoảng thời gian càng lúc càng ngắn. Thế nhưng thời gian trôi qua bất chấp cách chúng ta muốn chia tách nó một cách nhân tạo thành những khoảng thời gian nhỏ dần này. Việc nghĩ về thời gian, chứ không phải không gian, như một đường đứng yên có thể chia nhỏ vô hạn định là tốt (và chúng ta thường nghĩ tới thời gian theo kiểu này khi giải các bài tập vật lí), nhưng điểm mấu chốt là cách chúng ta cảm nhận thời gian không phải là một đường đứng yên như cách chúng ta có thể nhìn các đường thẳng trong không gian. Ta không thể đưa bản thân mình ra khỏi dòng chảy của thời gian. Thời gian cứ trôi bất chấp – và vì thế chúng ta chuyển động.
Nếu chúng ta xét tình huống từ góc nhìn của ai đó đang không chuyển động, mà bắt đầu từ trạng thái nghỉ, thì chúng ta phải nghĩ thêm một chút ít vật lí nữa. Đây là thứ chúng ta đã học ở trường (và đa số chúng ta, chẳng nghi ngờ gì cả, đã quên rất mau). Nó được gọi là định luật thứ hai của Newton, nó nói rằng để làm một vật bắt đầu chuyển động, cần có một lực tác dụng lên nó. Lực này sẽ gây cho nó gia tốc – làm thay đổi trạng thái của nó từ đứng yên thành chuyển động. Còn một khi nó đang chuyển động, thì áp dụng lập luận tương tự: đó là, khi thời gian trôi qua, quãng đường đi được dựa trên tốc độ của vật đang chuyển động, nó không nhất thiết không đổi. Lập luận Lưỡng phân khi đó chẳng nói lên điều gì về chuyển động thật trong thế giới vật chất.
Tôi nên đưa ra một nhận xét sau cùng trước khi tiếp tục. Thuyết tương đối của Albert Einstein dạy chúng ta rằng có lẽ chúng ta không nên bác bỏ Nghịch lí Lưỡng phân một cách tự tin như thế. Theo Einstein, thời gian có thể được xem xét theo kiểu tương tự với không gian – thật vậy, ông gọi thời gian là trục thứ tư, hay chiều thứ tư, của cái gọi là không-thời gian. Điều này cho thấy có lẽ thời gian xét cho cùng đúng là một ảo giác – và, nếu vậy, thì chuyển động cũng thế. Thế nhưng tôi sẽ cãi rằng, bất chấp sự thành công của thuyết tương đối, kết luận này đưa chúng ta xa rời vật lí học và tiến vào vùng nước u linh của siêu hình học – những ý tưởng trừu tượng không có sự hậu thuẫn chắc chắn của khoa học kinh nghiệm.
Tôi không nói thuyết tương đối của Einstein là sai; tất nhiên là không rồi. Chỉ có điều là các ý tưởng của Einstein thật ra chỉ hiển hiện khi vạn vật bắt đầu chuyển động rất nhanh – gần bằng tốc độ ánh sáng. Ở những tốc độ bình thường hằng ngày, chúng ta có quyền bỏ qua những hiệu ứng “tương đối tính” như thế và nghĩ về thời gian và không gian theo nghĩa quen thuộc thường ngày mà chúng ta vẫn quen dùng. Nói chung, nếu chúng ta đẩy lập luận của Zeno đến cực độ logic của nó, thì sẽ không đúng nếu nói thời gian và không gian có thể chia nhỏ vô hạn thành những khoảng nhỏ dần nhưng vẫn rời rạc. Ở một mức nào đó, vạn vật trở nên nhỏ đến mức vật lí lượng tử phát huy tác dụng, khi đó thời gian và không gian trở nên mờ nhạt và không thể xác định rạch ròi, và việc chia chúng thành những mảnh nhỏ dần là không còn ý nghĩa nữa. Quả vậy, trong địa hạt lượng tử của nguyên tử và các hạt hạ nguyên tử, chuyển động là một ảo giác mà thôi. Thế nhưng đó không phải thứ Zeno nghĩ đến.
Dù rằng vui vẻ thám hiểm và bàn luận trong ngữ cảnh này, nhưng cả vật lí lượng tử lẫn thuyết tương đối đều là không cần thiết để giải trừ Lưỡng phân của Zeno. Sử dụng những ý tưởng như vậy từ vật lí hiện đại để biện hộ rằng mọi chuyển động là ảo giác làm bỏ lỡ điểm mấu chốt và mang chúng ta đến gần một cách nguy hiểm biến vật lí học thành thần bí. Vì thế không nên làm cho mọi thứ phức tạp hơn chúng cần phải thế. Sẽ có nhiều thời gian hơn cho thứ quẫn trí như thế ở phần sau quyển sách, hãy tin tôi đi.
ĐƯỜNG ĐUA
Vậy chúng ta hãy nhanh chóng tiến lên. Một nghịch lí có liên quan đến Zeno đả động đến khái niệm tốc độ được gọi là Nghịch lí Hàng chuyển động. Nó có phần tối nghĩa và được mang đến chúng ta thông qua Aristotle, ông gọi nó là Nghịch lí Đường đua. Tôi sẽ cố mô tả nó cô đọng nhất có thể.
Hãy hình dung có ba đoàn tàu, mỗi đoàn gồm một toa máy và hai toa hàng. Đoàn tàu thứ nhất vẫn đứng yên trong nhà ga. Đoàn tàu thứ hai và thứ ba không dừng tại ga mà đang chuyển động ở tốc độ không đổi và bằng nhau theo chiều ngược nhau, B đi từ tây sang và C đi từ đông sang.
Tại một thời điểm cho trước, các đoàn tàu có vị trí như trên Hình 2.2(a). Sau đó một giây, chúng sắp thẳng hàng như Hình 2.2(b). Vấn đề, theo Zeno, liên quan đến chuyển động của đoàn tàu B: trong một giây, nó đi hết độ dài một toa hàng của đoàn tàu A, nhưng đồng thời nó đi hết độ dài hai toa hàng của đoàn tàu C. Nghịch lí là đoàn tàu B đã dịch chuyển một quãng đường và hai lần quãng đường đó trong cùng một thời gian. Hình như Zeno biết rõ đây chỉ là những quãng đường tương đối, thành ra ông cố tạo ra nghịch lí theo thời gian. Chia hai quãng đường đi được cho tốc độ không đổi của đoàn tàu B, ta được hai khoảng thời gian khác nhau, một khoảng gấp đôi khoảng kia. Thế nhưng cả hai khoảng đều có vẻ mâu thuẫn khi mô tả thời gian cần thiết đi từ tình huống trong hình trên đến tình huống sắp thẳng hàng trong hình dưới!
Hình 2.2 Nghịch lí Hàng chuyển động

(a) Đoàn tàu A đứng yên. Đoàn tàu B đi từ trái sang phải và đoàn tàu C đi từ phải sang trái ở tốc độ bằng với B.
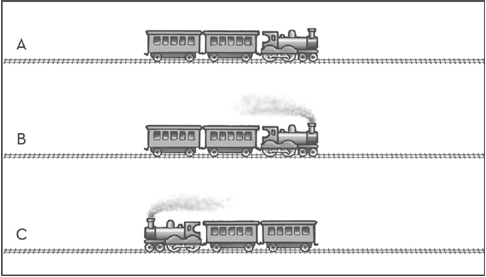
(b) Một giây sau, ba đoàn tàu sắp thẳng hàng với nhau.
Giải quyết nghịch lí biểu kiến này không khó, vì chúng ta có thể thấy cái sai trong lập luận trên. Có một thứ gọi là tốc độ tương đối, tất nhiên rồi, nên chúng ta không thể nói B đang chuyển động ở cùng một tốc độ so với C đang chuyển động như so với A đứng yên. Zeno có biết điều này không, hay chỉ là ông đang cố tạo ra một điểm tinh vi hơn về bản chất ảo giác của chuyển động? Thực hư không rõ; nhưng, như mỗi học sinh phổ thông đều hiểu, ở đây thật ra chẳng có nghịch lí gì hết. B đi qua C ở tốc độ tương đối gấp hai lần so với nó đi qua A, và vì thế tất nhiên nó sẽ đi qua hai toa hàng của C trong cùng thời gian mà nó đi qua một toa hàng của A.
MŨI TÊN
Giống như Lưỡng phân, đây là một nghịch lí khác tập trung vào ý tưởng nói rằng chuyển động thật chỉ là một ảo giác. Nó được Aristotle trình bày như sau: “Giả sử mọi thứ khi nó đứng yên chiếm giữ một không gian như nhau, và giả sử thứ đang chuyển động luôn chiếm giữ một không gian như thế tại thời điểm bất kì, thì do đó mũi tên đang bay là không chuyển động.”
Ơ? Vâng, hãy để tôi cố làm rõ thêm.
Một mũi tên đang bay, tại một thời điểm bất kì cho trước trong thời gian, có một vị trí nhất định, cố định – như chúng ta sẽ nhìn thấy trong một bức ảnh chụp nhanh. Còn nếu chúng ta chỉ nhìn thấy nó tại thời điểm này, thì nó sẽ không thể phân biệt với một mũi tên thật sự không chuyển động ở cùng vị trí đó. Vậy làm thế nào ta có thể nói một mũi tên đang chuyển động? Quả vậy, vì thời gian gồm một chuỗi những thời khắc liên tiếp, trong mỗi thời khắc đó mũi tên không chuyển động, nên nó không bao giờ chuyển động.
Nghịch lí, tất nhiên, là ở chỗ chúng ta biết có thứ gọi là chuyển động. Tất nhiên mũi tên chuyển động. Vậy thì đâu là lỗi logic trong nhận định của Zeno?
Thời gian có thể được xem là gồm một chuỗi những “thời khắc” vô cùng ngắn, ta có thể nghĩ đó là những khoảng thời gian nhỏ nhất có thể, không thể chia nhỏ được nữa. Là một nhà vật lí, tôi có thể nhìn thấy vấn đề với lập luận của Zeno. Nếu những thời khắc không thể chia nhỏ này không chính xác có độ dài zero (những ảnh chụp nhanh thật sự) thì mũi tên sẽ ở một vị trí hơi khác lúc bắt đầu mỗi thời khắc so với vị trí của nó lúc kết thúc, và do đó không thể nói nó đứng yên được. Mặt khác, nếu những thời khắc như thế thật sự có độ dài zero, thì không quan trọng có bao nhiêu thời khắc xếp liền cạnh nhau, chúng sẽ không bao giờ cộng lại thành một khoảng thời gian khác zero: ta có thể cộng zero với chính nó bao nhiêu lần tùy thích và đáp số vẫn là zero. Vậy nên lập luận của Zeno rằng một khoảng thời gian hữu hạn được cấu thành bởi một chuỗi thời khắc liên tiếp như thế là sai.
Cần những tiến bộ trong toán học cũng như trong vật lí học thì nghịch lí này cuối cùng mới yên nghỉ. Đặc biệt hơn, chính việc tìm hiểu giải tích, lĩnh vực toán học được phát triển bởi Isaac Newton và nhiều người khác vào thế kỉ mười bảy, nó mô tả cách cộng những đại lượng vô cùng nhỏ để mô tả đúng khái niệm biến thiên, nó đã đưa những ý tưởng chất phác của Zeno vào yên nghỉ.
Vâng, gần như vậy. Vào năm 1977, hai nhà vật lí tại Đại học Texas công bố một bài báo nghiên cứu bất ngờ đề xuất rằng Nghịch lí Mũi tên của Zeno có lẽ đã bị dẹp quá hấp tấp. Tên của họ là Baidyanaith Misra và George Sudarshan, và tiêu đề bài báo của họ là “Nghịch lí Zeno trong Thuyết Lượng tử”. Các nhà vật lí trên khắp thế giới một phen bất ngờ. Một số người nghĩ công trình trên thật ngớ ngẩn, còn một số khác thì đổ xô thử kiểm tra ý tưởng đó. Thế nhưng trước khi tôi trình bày thêm, cho phép tôi nói đôi điều ít ỏi mà tôi cảm nhận được mình có thể tránh được ở phần đầu này của quyển sách về một tập hợp ý tưởng mới lạ và tuyệt vời, đó là cơ học lượng tử.
NGHỊCH LÍ ZENO VÀ CƠ HỌC LƯỢNG TỬ
Cơ học lượng tử là lí thuyết mô tả sự vận hành của thế giới vi mô – với từ vi mô, tôi không có ý nói tới thế giới tí hon chỉ có thể nhìn thấy dưới kính hiển vi, mà là thế giới bé nhỏ hơn rất, rất nhiều của các nguyên tử và phân tử và các hạt hạ nguyên tử (electron, proton, và neutron) cấu tạo nên chúng. Thật vậy, cơ học lượng tử là tập hợp toán học gồm những ý tưởng quyền năng nhất, quan trọng nhất, và căn bản nhất trong toàn thể khoa học. Nó nổi bật vì hai lí do có vẻ mâu thuẫn nhau (bản thân nó gần như là một nghịch lí!) Một mặt, nó căn bản cho sự hiểu biết của chúng ta về sự vận hành của thế giới nên nó ngự tại tâm điểm của đa số những tiến bộ công nghệ xảy ra trong nửa thế kỉ vừa qua. Mặt khác, dường như chẳng ai biết chính xác nó có ý nghĩa gì.
Tôi phải làm rõ từ đầu rằng lí thuyết về cơ học lượng tử tự nó không hề lạ lùng hay phản logic; trái lại, nó là một công trình đẹp chính xác và logic mô tả tự nhiên một cách tuyệt vời. Không có nó chúng ta sẽ không thể nào hiểu được cơ sở của hóa học hiện đại, hay điện tử học, hay khoa học vật liệu; chúng ta đã không phát minh ra chip silicon hay laser; sẽ chẳng có ti vi, máy vi tính, lò vi sóng, máy hát đĩa CD và DVD, hay điện thoại di động, sẽ không có nhiều thứ khác nữa mà chúng ta chào đón trong thời đại công nghệ của mình.
Cơ học lượng tử dự đoán và giải thích chính xác hành trạng của mỗi viên gạch cấu trúc của vật chất với độ chuẩn xác cực kì. Nó đưa chúng ta đến chỗ hiểu biết rất chính xác và gần như hoàn chỉnh về cách thế giới hạ nguyên tử hành xử, và cách vô số hạt tương tác với nhau và kết nối để tạo thành thế giới mà chúng ta thấy xung quanh mình, và thế giới mà tất nhiên chúng ta là một bộ phận trong đó. Xét cho cùng, chúng ta rốt lại chỉ là một tập hợp gồm hàng nghìn tỉ nguyên tử tuân theo các quy tắc của cơ học lượng tử và được tổ chức theo một cách vô cùng phức tạp.
Những quy tắc toán học kì lạ này đã được khám phá vào thập niên 1920. Hóa ra chúng rất khác với các quy tắc chi phối thế giới trần tục thường ngày mà chúng ta quen thuộc: thế giới của những vật mà chúng ta thấy xung quanh mình. Gần cuối sách, tôi sẽ khảo sát mức độ lạ lùng của một số quy tắc này khi chúng ta xét Nghịch lí Con mèo của Schrödinger. Từ lúc này, tôi muốn tập trung vào một đặc điểm hết sức kì lạ của thế giới lượng tử, đó là một nguyên tử nếu rời khỏi dụng cụ của chúng ta sẽ hành xử khác với khi nó được “quan sát” - ở đây tôi muốn nói rằng khi nó đang được theo dõi bằng một cách nào đó: bị thúc hoặc đẩy, bị đập hoặc vụt. Đặc trưng này của thế giới lượng tử vẫn chưa được hiểu đầy đủ, một phần là vì lúc này người ta vẫn đang làm rõ chính xác thì cái gì cấu thành “quan sát” hiểu theo nghĩa này. Vấn đề này được gọi là “bài toán đo lường” và nó vẫn là một lĩnh vực sôi nổi trong nghiên cứu khoa học ngày nay.
Thế giới lượng tử bị chi phối bởi sự ngẫu nhiên và xác suất. Đó là nơi chẳng giống chút nào với vẻ ngoài của nó. Nếu để đơn độc, một nguyên tử phóng xạ sẽ phát ra một hạt, nhưng chúng ta không thể dự đoán khi nào hiện tượng này sẽ xảy ra. Tất cả những gì chúng ta có thể làm là tính ra một con số gọi là chu kì bán rã. Đây là thời gian cần thiết cho một nửa của một số lượng lớn nguyên tử giống hệt nhau “phân rã” phóng xạ. Số lượng nguyên tử càng lớn, thì chúng ta có thể tính càng chính xác chu kì bán rã này, nhưng chúng ta không bao giờ có thể dự đoán trước nguyên tử nào trong mẫu sẽ phân rã tiếp theo. Nó y hệt như thống kê việc tung đồng xu. Chúng ta biết rằng nếu ta tung đồng xu hết lần đến lần khác, thì một nửa thời gian nó sẽ sấp và một nửa thời gian nó sẽ ngửa. Chúng ta gieo đồng xu càng nhiều lượt, thì dự đoán thống kê này sẽ càng chính xác. Nhưng chúng ta không bao giờ có thể dự đoán lần gieo đồng xu tiếp theo sẽ là sấp hay ngửa.
Thế giới lượng tử mang bản chất xác suất không phải vì cơ học lượng tử là một lí thuyết chưa hoàn chỉnh hay gần đúng, mà vì bản thân nguyên tử không “biết” khi nào thì sự kiện ngẫu nhiên này sẽ xảy ra. Đây là một ví dụ của cái gọi là “phi tất định luận”, hay phi dự báo.
Bài báo của Misra và Sudarshan, đăng trên Journal of Mathematical Physics, mô tả tình huống lạ lùng trong đó một nguyên tử phóng xạ, nếu được quan sát chặt chẽ và liên tục, sẽ không bao giờ phân rã! Ý tưởng đó có thể được tóm tắt hoàn hảo bởi câu châm ngôn “cái ấm bị ngó không bao giờ sôi”, theo tôi biết thì câu này được sử dụng lần đầu tiên bởi nhà văn thời Victoria, Elizabeth Gaskell trong quyển tiểu thuyết năm 1848 của bà, Mary Barton – mặc dù có lẽ phải xếp nó vào loại có nguồn gốc lâu đời hơn. Ý tưởng trên có nguồn gốc của nó, tất nhiên, ở Nghịch lí Mũi tên của Zeno và sự bất lực của chúng ta muốn phát hiện chuyển động bằng cách xét ảnh chụp nhanh của một vật đang chuyển động trong một khoảnh khắc.
Thế nhưng làm thế nào và tại sao điều này có thể xảy ra trên thực tế? Rõ ràng việc nói cái ấm bị ngó chẳng gì hơn là một bài học đơn giản về lòng kiên nhẫn: bạn không thể làm cho một ấm nước sôi nhanh lên chút nào bằng cách ngó chằm chằm vào nó. Tuy nhiên, có vẻ như Misra và Sudarshan đang đề xuất rằng khi đến với các nguyên tử, bạn thật sự làm ảnh hưởng đến cách chúng hành xử bởi việc quan sát chúng. Ngoài ra, sự can nhiễu này là không thể tránh khỏi – hành động nhìn sẽ không tránh khỏi làm thay đổi trạng thái của thứ bạn đang nhìn.
Ý tưởng của họ chạm tới tâm điểm của cách cơ học lượng tử mô tả thế giới vi mô: là một thực tại mờ nhạt, ma quái trong đó mọi thứ lạ lùng sắp diễn ra có vẻ như diễn ra bình thường khi nó được để cho đơn độc – một ý tưởng chúng ta sẽ gặp lại ở Chương 9 – không một thứ nào trong số đó chúng ta có thể phát hiện đang thật sự diễn ra. Thế nên một nguyên tử, nếu rời khỏi dụng cụ của chúng ta, sẽ tự phát phát ra một hạt tại một thời điểm bất kì, sẽ vì lí do nào đó mà xấu hổ không làm thế nữa nếu nó đang bị dòm ngó, vậy nên chúng ta không bao giờ có thể thật sự bắt gặp nó đang hành động. Cứ như thể nguyên tử được ban cho một kiểu nhận thức nào đó, thật điên rồ. Thế nhưng thế giới lượng tử vốn điên rồ. Một trong những cha đẻ của thuyết lượng tử là nhà vật lí Đan Mạch Niels Bohr, người hồi năm 1920 đã thành lập một viện nghiên cứu ở Copenhagen nhờ đó ông thu hút những thiên tài khoa học vĩ đại nhất thời ấy – những con người như Werner Heisenberg, Wolfgang Pauli, và Erwin Schrödinger – cố gắng giải mã bí ẩn của những viên gạch cấu trúc nhỏ bé nhất của tự nhiên. Một trong những câu nói nổi tiếng của Bohr là “nếu bạn không cảm thấy kinh ngạc trước những kết luận của cơ học lượng tử thì bạn chẳng hiểu gì về nó hết”.
Bài báo của Misra và Sudarshan mang tiêu đề “Nghịch lí Zeno trong Thuyết Lượng tử” vì nguồn gốc của nó ở Nghịch lí Mũi tên. Tuy nhiên, công bằng mà nói thì, trong khi kết luận của nó vẫn có phần gây tranh cãi, nhưng đối với đa số nhà vật lí nó không còn là một nghịch lí nữa. Trong văn đàn ngày nay, nó được gọi thông dụng hơn là “Nghịch lí Zeno Lượng tử”, và ta thấy nó được áp dụng rộng rãi hơn so với trong tình huống mà Misra và Sudarshan mô tả. Một nhà vật lí lượng tử sẽ vui vẻ nói với bạn rằng hiệu ứng này có thể được giải thích bởi “sự suy sụp liên tục của hàm sóng vào trạng thái chưa phân rã lúc ban đầu”, đó là kiểu hành văn cầu kì khó hiểu mà người ta trông đợi từ những người như thế – tôi biết thế, vì tôi là một trong số họ. Song tôi không nghĩ tôi sẽ theo đuổi hướng suy nghĩ này cụ thể hơn chút nào nữa ở đây, trong trường hợp bạn đang lo lắng tự hỏi chẳng biết mình đang phiêu lưu đến đâu.
Khám phá mới đây này về Hiệu ứng Zeno Lượng tử hiện diện khắp nơi nơi là do các nhà vật lí lượng tử đã hiểu rõ hơn cách nguyên tử phản ứng với môi trường xung quanh của nó. Một đột phá lớn được thực hiện khi các nhà khoa học tại một trong những phòng thí nghiệm danh giá nhất thế giới, Viện Tiêu chuẩn và Công nghệ Quốc gia ở Colorado, xác nhận Hiệu ứng Zeno Lượng tử trong một thí nghiệm nổi tiếng hồi năm 1990. Thí nghiệm diễn ra tại nơi có tên gọi thật tuyệt là Phân viện Thời gian và Tần số, nơi nổi tiếng nhất với việc ấn định các tiêu chuẩn đo lường thời gian chính xác nhất. Thật vậy, các nhà khoa học ở đây mới đây đã chế tạo đòng hồ nguyên tử chính xác nhất thế giới, chỉ sai lệch một giây trong ba tỉ rưỡi năm – gần tương đương với tuổi của chính Trái đất.
Một trong những nhà vật lí nghiên cứu về những đồng hồ vô cùng chính xác này là Wayne Itano. Chính nhóm của ông đã thiết kế thí nghiệm kiểm tra xem Hiệu ứng Zeno Lượng tử thật sự có thể phát hiện được hay không. Thí nghiệm cho bắt giữ vài nghìn nguyên tử trong một từ trường, sau đó vụt chúng thật nhẹ nhàng bằng laser, buộc chúng từ bỏ bí mật của chúng. Với mức tin cậy đủ mức, các nhà nghiên cứu tìm thấy bằng chứng rõ ràng của Hiệu ứng Zeno Lượng tử: dưới sự quan sát liên tục, các nguyên tử hành xử rất khác với những gì các nhà khoa học từng trông đợi.
Một bước ngoặc cuối cùng: ngày nay có bằng chứng cho hiệu ứng ngược lại, cái gọi là “Hiệu ứng Phản Zeno”, đó là tương đương lượng tử của việc ngó chằm chằm vào một ấm nước và làm cho nó sôi nhanh hơn. Trong khi vẫn có phần suy đoán, nghiên cứu như thế đã chạm tới tâm điểm của một số lĩnh vực khoa học nổi bật nhất và có lẽ quan trọng nhất của thế kỉ hai mươi mốt, ví dụ như nghiên cứu hướng tới xây dựng cái gọi là máy tính lượng tử. Đây là dụng cụ khai thác trực tiếp một số hành trạng kì lạ của thế giới lượng tử để thực hiện các phép tính của nó một cách hiệu quả hơn nhiều.
Tôi không chắc Zeno xứ Elea sẽ làm gì với sự hồi sinh của những nghịch lí của ông, hoặc với tên tuổi của ông gắn liền với một hiện tượng nổi bật trong vật lí học gần hai nghìn rưỡi năm về sau. Ở đây, sự nghịch lí chẳng liên quan gì với các thủ thuật logic hết, mà mọi thứ liên quan đến những thủ thuật còn lạ lùng hơn nữa mà tự nhiên hình như có thể bày ra ở cấp độ tí hon của các nguyên tử – những thủ thuật mà chúng ta chỉ mới bắt đầu hiểu được.
Các nghịch lí Zeno đưa chúng ta đi từ thuở hồng hoang của vật lí học đến những ý tưởng cấp tiến trong thế kỉ hai mươi mốt. Toàn bộ những nghịch lí khác trong quyển sách này đều nảy sinh đâu đó trong khoảng thời gian lưng chừng giữa hai mốc trên. Để giải thích chúng, ta sẽ phải du hành đến những ranh giới xa xôi nhất của Vũ trụ và thám hiểm bản chất cốt lõi của chính không gian và thời gian. Hãy bám chặt nhé.
Trích từ Nghịch lí: 9 bí ẩn lớn nhất vật lí học (Jim Al-Khalili). Bản dịch của Thuvienvatly.com.