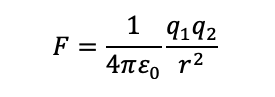Charles-Augustin de Coulomb (1736–1806), nhà vật lí Pháp nổi tiếng với định luật mô tả lực tương tác giữa hai điện tích điểm.
HIẾU KÌ. Sở trường kĩ thuật của Coulomb giữ một vai trò lớn trong việc xây dựng công sự Martinique, một hòn đảo ở Caribbean. yC là đơn vị chính thức cho yocto-coulomb, bằng 10–24 coulomb. Coulomb giành giải thưởng của Viện hàn lâm Khoa học Pháp cho phương pháp tốt nhất chế tạo la bàn dành cho tàu thuyền.
Những đóng góp của Coulomb cho khoa học về lực ma sát là vô cùng to lớn. Không hề cường điệu, người ta có thể nói rằng ông đã sáng lập lĩnh vực khoa học này.
- I.V. Kragelsky và V.S. Schedrov, Sự phát triển của khoa học về ma sát.
Có thể xem Coulomb là một trong những kĩ sư vĩ đại nhất ở châu Âu thế kỉ mười tám.
- C. Stewart Gillmor, “Charles Coulomb”, trong Từ điển tiểu sử khoa học.
Ai có thể quên được cái lần “Chuck” Coulomb thuyết trình trước Viện hàn lâm Khoa học ở Paris năm 1773 khi ông bàn về lí thuyết cơ học đất tiên phong?
- Terence Meany và Matthew Tirschwell, Hướng dẫn sửa chữa điện toàn tập dành cho dân không chuyên.
Charles-Augustin de Coulomb là một trong những nhà vật lí và kĩ sư lỗi lạc nhất của mọi thời đại có đóng góp cho các lĩnh vực điện học, từ học, cơ học ứng dụng, lực ma sát, và lực xoắn. Coulomb sinh ra trong một gia đình khá giả ở Angoulême ở tây nam nước Pháp. Sau đó gia đình ông chuyển đến Paris, ông vào học trường Collège Mazarin. Ông được hưởng một nền giáo dục phổ thông tốt về nhân chủng học, cũng như toán học, thiên văn học, và hóa học.
Có một dạo, cha ông mất trắng tiền bạc trong đầu cơ tài chính. Tình trạng khó khăn này, cộng với sự bất đồng của Coulomb với mẹ ông về các dự tính nghề nghiệp, làm cho gia đình ông li tán, Coulomb cùng cha chuyển đến Montpellier còn mẹ ông vẫn ở lại Paris. Theo một số nguồn thông tin, mẹ Coulomb muốn ông trở thành một bác sĩ, còn cậu con trai của bà nhất quyết đòi học một chuyên ngành định lượng hơn như là kĩ thuật hoặc toán học. Các bất đồng dần trở nên nảy lửa, và mẹ ông hầu như không thèm nhìn mặt ông.
Năm 1760, Coulomb vào học trường École du Génie tại Mézières và sau đó tốt nghiệp kĩ sư trong hàng ngũ đại úy hải quân trong Quân đoàn Kĩ sư (Corps du Génie). Trong hai thập niên sau đó, ông đã chu du khắp nơi, ở đâu ông cũng tham gia vào kĩ thuật cấu trúc, thiết kế công sự, và cơ học đất – chẳng hạn, ông đã dành ra vài năm ở West Indies với vai trò kĩ sư quân sự – trước khi trở lại Pháp, nơi ông bắt đầu viết các bài báo quan trọng về cơ học ứng dụng.
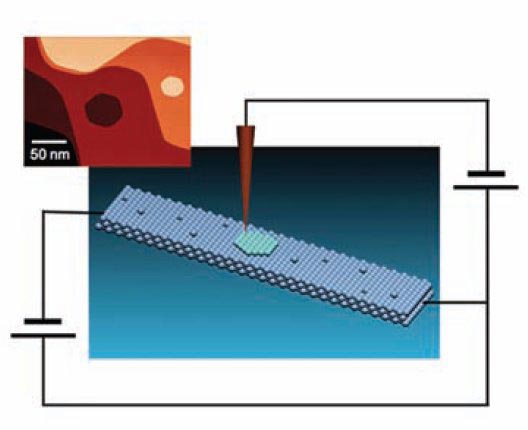
Coulomb đã chế tạo một cân xoắn vào khoảng năm 1777 để đo lực tĩnh điện. Cân xoắn gồm hai quả cầu kim loại gắn với một thanh cách điện. Thanh được treo tại ngay giữa của nó bằng một sợi tơ hoặc sợi chỉ mảnh không dẫn điện. Để đo lực điện, một trong hai quả cầu được làm cho nhiễm điện. Một quả cầu thứ ba có điện tích giống như vậy được đặt gần quả cầu nhiễm điện của cân, làm cho quả cầu trên cân bị đẩy ra. Lực đẩy này làm cho sợi tơ xoắn đi một lượng nhất định. Nếu chúng ta đo xem cần một lực bao nhiêu để làm xoắn sợi dây một góc bằng như vậy, thì ta có thể ước tính mức độ lực gây ra bởi quả cầu nhiễm điện. Nói cách khác, sợi dây tác dụng như một lò xo rất nhạy cung cấp một lực tỉ lệ thuận với góc xoắn. Coulomb chỉ ra rằng lực biến thiên theo 1/r2 đối với lực đẩy giữa các điện tích cùng dấu, và lực hút giữa các điện tích trái dấu, cách nhau khoảng r lúc ban đầu. Hình như chưa bao giờ ông thật sự chứng minh được rằng lực giữa các điện tích tỉ lệ thuận với tích các giá trị điện tích – ông chỉ đơn giản thừa nhận điều này là đúng. C. Stewart Gillmor, viết trong Từ điển tiểu sử khoa học, chỉ ra mức độ mà cân xoắn của Coulomb ảnh hưởng đến nền khoa học trong nhiều thế hệ:
Giải phép đơn giản, đẹp đẽ của Coulomb cho vấn đề lực xoắn trong bình trụ [với thang chia] và việc ông sử dụng cân xoắn trong các ứng dụng vật lí có ý nghĩa quan trọng đối với vô số nhà vật lí trong những năm tiếp theo… Coulomb đã phát triển một lí thuyết về lực xoắn trong những sợi tơ mảnh và sợi tóc. Ở đây ông là người đầu tiên chỉ ra cách dây treo xoắn có thể đem lại cho các nhà vật lí một phương pháp đo chính xác những lực cực kì nhỏ.
Đặc biệt, Coulomb đã chỉ ra với thí nghiệm của ông rằng số mũ của r (khoảng cách giữa hai điện tích) là bằng 2 với sai số một vài phần trăm. Ngày nay, chúng ta biết số mũ đó bằng 2 với sai số 2 phần 109.
Năm 1779, Coulomb bắt đầu nghiên cứu của ông về lực ma sát, cuối cùng đưa ông đến công bố quan trọng Théorie des machines simples, en ayant égard au frottement de leurs parties et à la raideur des cordages (Lí thuyết về các máy đơn giản, xét đến lực ma sát giữa các bộ phận của chúng và độ cứng của các khớp nối). Công trình này được tiếp nối bởi một chuyên luận về lực nhớt hai mươi năm sau đó. Định luật Coulomb về lực ma sát nói rằng đối với hai bề mặt chuyển động tương đối, lực ma sát động hoàn toàn độc lập với tốc độ tương đối của hai bề mặt.
Nghiên cứu của Coulomb về lực ma sát được khích lệ bởi giải thưởng của Viện hàn lâm Khoa học ở Paris dành cho “giải pháp về lực ma sát trượt và các bề mặt lăn, chống lại sự bẻ cong ở dây thừng, và áp dụng những giải pháp này cho các máy đơn giản dùng trong hải quân”. Theo Peter J. Plau, viết trong Khoa học Ma sát và Công nghệ:
Các nghiên cứu và kết luận của Coulomb về bản chất của lực ma sát đã thống trị tư tưởng trong lĩnh vực này trong hơn một thế kỉ rưỡi, và nhiều khái niệm của ông vẫn còn được sử dụng. Thật vậy, thuật ngữ “lực ma sát Coulomb” vẫn được tìm thấy trong các ấn phẩm giải thích các kết quả thí nghiệm gần đây…
Từ 1785 đến 1791, Coulomb viết bảy bài báo quan trọng về lực điện và lực từ, và ông gửi chúng cho Viện hàn lâm Khoa học. Các chủ đề bao gồm việc ông tiếp tục sử dụng cân xoắn để tìm hiểu lực hút, lực đẩy, phân bố của dòng điện trên bề mặt các vật mang điện, và minh chứng của ông về quy luật nghịch đảo bình phương của các cực từ. Công trình năm 1785 của ông, mô tả việc ông sử dụng các loại cân xoắn khác nhau, được công bố trong ấn phẩm của ông, Recherches théoriques et expérimentales sur la force de torsion et sur l’élasticité des fils de metal (Nghiên cứu lí thuyết và thực nghiệm về ứng suất xoắn và suất đàn hồi của các dây kim loại). Ở đây, ông chỉ ra rằng có thể dùng cân xoắn để đo chính xác các lực cực kì nhỏ.
Năm 1802, Coulomb cưới Louise Françoise LeProust Desormeaux, mẹ của hai con trai ông trước khi họ cưới. Louise đang ở độ tuổi đôi mươi. Về cuối đời mình, Coulomb đặc biệt thích sống ở miền quê và dạy khoa học cho cậu con con út, Charles. Vào những ngày cuối đời mình, Coulomb bị sốt và cuối cùng thì qua đời. Tang lễ của ông được tổ chức tại Abbaye de St.-Germain-des-Prés.
Về năng lực khoa học của Coulomb, Ioan James viết trong Các nhà vật lí danh tiếng: Từ Galileo đến Yukawa như sau:
Ông được mô tả là một nhà vật lí hoàn mĩ, sánh ngang vào thế kỉ mười tám chỉ có Henry Cavendish, kết hợp kĩ năng thực nghiệm, độ chuẩn xác đo lường, và căn bản toán học tốt đủ cho mọi nhu cầu của ông.
Một hố va chạm trên mặt trăng có đường kính 89 km được đặt tên Coulomb và được Tổng Liên đoàn Thiên văn Quốc tế phê chuẩn vào năm 1970.
Trong sự nghiệp của mình, Coulomb đã tiến hành các nghiên cứu đa dạng và có nhiều đóng góp cho kiến thức của chúng ta về
- Sự nứt vỡ của các trụ và dầm
- Sự cong vểnh của các vật liệu giòn
- Cơ sở vật lí của nhịp cuốn hình vòm
- Sự ma sát của máy móc và lực cản trong chất lỏng
- Thiết kế cối xay gió
- Sự đàn hồi của kim loại và sợi tơ mảnh, và cơ học đất
- Thiết kế la bàn từ
- Hiệu quả của công nhân con người và động vật (tối ưu nhân tố)
Một vài người đã tìm thấy mặt này mặt kia của Định luật Coulomb trước cả Coulomb. Như tận năm 1750, người Anh Reverend John Michell (1724–1793) đã công bố các nghiên cứu chỉ ra rằng lực hút và lực đẩy giữa các cực nam châm biến thiên tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Cân xoắn của Michell sau đó được Henry Cavendish (1731-1810) dùng để đo tỉ trọng của Trái Đất. Coulomb phát minh ra cân xoắn của ông vào khoảng năm 1784, và mặc dù công trình của Michell có lẽ đi trước Coulomb, nhưng các khám phá của họ là độc lập.
John Robinson (1725-?), một bác sĩ người Anh, đã đo lực hút và đẩy tĩnh điện vào năm 1769, các thí nghiệm của ông cho thấy lực đẩy điện phụ thuộc 1/r2,06, và lực hút điện phụ thuộc 1/rc, trong đó c < 2. Từ những kết quả này, ông đề xuất rằng có lẽ 1/r2 là đúng. Đồng thời, nhà hóa học Anh Joseph Priestly (1733-1804) đã đề xuất quy luật 1/r2 của lực điện. Priestly đã viết trong Lịch sử và hiện trạng về Điện học như sau:
Có lẽ chúng ta không nên suy luận từ thí nghiệm này [với các vật dẫn rỗng tích điện] rằng lực hút điện tuân theo quy luật giống với lực hấp dẫn và do đó phụ thuộc theo bình phương khoảng cách; vì như thế dễ dàng chứng tỏ rằng Trái Đất có dạng một lớp vỏ, một vật thể mà ở bên trong nó sẽ không bị hút về một phía nhiều hơn phía kia?
Mặc dù Priestly chẳng nêu ra bằng chứng thuyết phục cho Định luật Coulomb, song những suy đoán của ông về cơ bản là đúng. Priestly còn độc lập phát minh ra cân xoắn và dùng nó để chỉ ra rằng lực giữa hai cực nam châm biến theo theo nghịch đảo bình phương khoảng cách giữa hai cực.
Ngày nay, chúng ta gọi quy luật 1/r2 là Định luật Coulomb để tôn vinh những kết quả độc lập mà Coulomb thu được thông qua bằng chứng do hệ thống cân xoắn của ông đem lại. Nói cách khác, Coulomb đã cung cấp các kết quả định lượng có tính thuyết phục cho một điều mà mãi đến năm 1785 thường chỉ là một suy đoán tốt.
Lực Coulomb cũng thích ứng ở cấp độ nguyên tử, và thật vậy, để có thông tin ta hãy so sánh lực hấp dẫn với lực Coulomb đối với nguyên tử hydrogen. Lấy gần đúng, ta xem electron là một hạt điểm quay xung quanh hạt điểm proton, với khoảng cách trung bình giữa electron và proton là 5,3 × 10–11 mét, lực Coulomb có thể được tính bởi
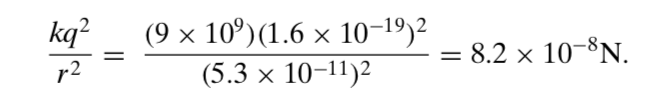
Độ lớn của lực hấp dẫn Fg giữa proton và electron có thể được tính gần đúng bằng khối lượng electron me và khối lượng proton mp:

Lưu ý rằng lực Coulomb lớn hơn rất nhiều so với lực hấp dẫn giữa hai hạt hạ nguyên tử này.
Tóm lại, lưu ý rằng Tháp Eiffel ở Paris có vinh danh tên tuổi của 72 nhà khoa học Pháp vĩ đại và các nhà tư tưởng khác – trong đó có Coulomb. Những chữ khắc ban đầu của Gustave Eiffel về những cái tên này đã bị sơn phủ vào đầu thế kỉ hai mươi song đã được phục hồi vào năm 1987. Các chữ cái khắc tên ấy có chiều cao xấp xỉ 60 centi-mét. Trong danh sách dưới đây, tôi in đậm tên của những người có liên quan trong quyển sách này (chỉ tính những cái tên còn lại trên tháp).
1. Ampère (André-Marie Ampère, nhà toán học và nhà vật lí)
2. Arago (Dominique François Jean Arago, nhà thiên văn học và nhà vật lí)
3. Barral (Jean-Augustin Barral, nhà nông học, nhà hóa học, nhà vật lí)
4. Becquerel (Antoine Henri Becquerel, nhà vật lí)
5. Bélanger (Jean-Baptiste-Charles-Joseph Bélanger, nhà toán học)
6. Belgrand (Eugene Belgrand, kĩ sư)
7. Berthier (Pierre Berthier, nhà khoáng vật học)
8. Bichat (Marie François Xavier Bichat, nhà giải phẫu học và nhà sinh lí học)
9. Borda (Jean-Charles de Borda, nhà toán học)
10. Breguet (Abraham Louis Breguet, thợ máy và nhà phát minh)
11. Bresse (Jacques Antoine Charles Bresse, kĩ sư dân sự và kĩ sư thủy lực)
12. Broca (Paul Pierre Broca, thầy thuốc và nhà nhân chủng học)
13. Cail (Jean-François Cail, nhà tư bản công nghiệp)
14. Carnot (Nicolas Léonard Sadi Carnot, nhà toán học)
15. Cauchy (Augustin Louis Cauchy, nhà toán học)
16. Chaptal (Jean-Antoine Chaptal, nhà nông học và nhà hóa học)
17. Chasles (Michel Chasles, nhà hình học)
18. Chevreul (Michel Eugène Chevreul, nhà hóa học)
19. Clapeyron (Émile Clapeyron, kĩ sư)
20. Combes (Émile Combes, kĩ sư và nhà luyện kim)
21. Coriolis (Gaspard-Gustave Coriolis, kĩ sư và nhà khoa học)
22. Coulomb (Charles-Augustin de Coulomb, nhà vật lí)
23. Cuvier (Baron Georges Leopold Chretien Frédéric Dagobert Cuvier, nhà tự nhiên học)
24. Daguerre (Louis Daguerre, nghệ sĩ và nhà hóa học)
25. De Dion (Albert de Dion, kĩ sư)
26. De Prony (Gaspard de Prony, kĩ sư)
27. Delambre (Jean Baptiste Joseph Delambre, nhà thiên văn học)
28. Delaunay (Charles-Eugène Delaunay, nhà thiên văn học)
29. Dulong (Pierre Louis Dulong, nhà vật lí và nhà hóa học)
30. Dumas (Jean Baptiste André Dumas, nhà hóa học)
31. Ebelmen (Jean-Jacques Ebelmen, nhà hóa học)
32. Fizeau (Hippolyte Fizeau, nhà vật lí)
33. Flachat (Jeugène Flachat, kĩ sư)
34. Foucault (Léon Foucault, nhà vật lí)
35. Fourier (Jean Baptiste Joseph Fourier, nhà toán học)
36. Fresnel (Augustin-Jean Fresnel, nhà vật lí)
37. Gay-Lussac (Joseph Louis Gay-Lussac, nhà hóa học)
38. Giffard (Henri Giffard, kĩ sư)
39. Goüin (Ernest Goüin, kĩ sư và nhà tư bản công nghiệp)
40. Haüy (René-Just Haüy, nhà khoáng vật học)
41. Jamin (Jules Célestin Jamin, nhà vật lí)
42. Jousselin (Alexandre Louis Jousselin, kĩ sư)
43. Lagrange (Joseph Louis Lagrange, nhà toán học)
44. Lalande (Joseph Jérôme Lefrançais de Lalande, nhà thiên văn học)
45. Lamé (Gabriel Lamé, nhà hình học)
46. Laplace (Pierre-Simon Laplace, nhà toán học và nhà thiên văn học)
47. Lavoisier (Antoine Lavoisier, nhà hóa học)
48. Le Chatelier (Henri Louis le Chatelier, nhà hóa học)
49. Le Verrier (Urbain Le Verrier, nhà thiên văn học)
50. Legendre (Adrien-Marie Legendre, nhà hình học)
51. Malus (Etienne-Louis Malus, physicist)
52. Monge (Gaspard Monge, nhà hình học)
53. Morin (Jean-Baptiste Morin, nhà toán học và nhà vật lí học)
54. Navier (Claude-Louis Marie Henri Navier, nhà toán học)
55. Petiet (Jules Petiet, kĩ sư)
56. Pelouze (Théophile-Jules Pelouze, nhà hóa học)
57. Perdonnet (Albert Auguste Perdonnet, kĩ sư)
58. Perrier (François Perrier, nhà địa lí và nhà toán học)
59. Poinsot (Louis Poinsot, nhà toán học)
60. Poisson (Simeon Poisson, nhà toán học và nhà vật lí)
61. Polonceau (Antoine-Rémi Polonceau, kĩ sư)
62. Poncelet (Jean-Victor Poncelet, nhà hình học)
63. Regnault (Henri Victor Regnault, nhà hóa học và nhà vật lí)
64. Sauvage (Jean-Pierre Sauvage, thợ máy)
65. Schneider (Jacques Schneider, nhà tư bản công nghiệp)
66. Seguin (Marc Seguin, thợ máy)
67. Sturm (Jacques Charles François Sturm, nhà toán học)
68. Thénard (Louis Jacques Thénard, nhà hóa học)
69. Tresca (Henri Tresca, kĩ sư và thợ máy)
70. Triger (Jacques Triger, kĩ sư)
71. Vicat (Louis Vicat, kĩ sư)
72. Wurtz (Charles-Adolphe Wurtz, nhà hóa học)
ĐỌC THÊM
Blau, Peter J., Friction Science and Technology (New York: Marcel Dekker, 1995).
Elert, Glenn, “Dielectrics,” trong The Physics Hypertextbook; xem hypertextbook. com/physics/electricity/dielectrics/.
Gillmor, C. Stewart, “Charles Coulomb,” trong Dictionary of Scientific Biography, Charles Gillispie, biên tập chính (New York: Charles Scribner’s Sons, 1970).
James, Ioan, Remarkable Physicists: From Galileo to Yukawa (New York: Cambridge University Press, 2004).
Kovacs, J., “Coulomb’s Law,” Project PHYSNET, Michigan State University; xem physnet.org/modules/pdfmodules/m114.pdf.
Priestley, Joseph, The History and Present State of Electricity (London: J. Doddsley, J. Johnson, B. Davenport, & T. Cadell, 1767).
Shamos, Morris, Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein (New York: Dover, 1987).
Wikipedia, “The 72 Names on the Eiffel Tower”; xem en.wikipedia.org/wiki/ The_72_names_on_the_Eiffel_Tower.
LUẬN BÀN
Từng sự thật được chọn lọc và nhóm lại với nhau sao cho các kết nối hợp lẽ của chúng trở nên tường minh. Bằng cách nhóm những quy luật này với nhau, người ta có thể thu được những quy luật khác tổng quát hơn… Tuy nhiên… những tiến bộ lớn về tri thức khoa học chỉ hình thành [bằng phương pháp quy nạp] đến một mức nhỏ nào đó. Nếu một nghiên cứu là tiếp cận thứ gì đó mà không có quan điểm định trước, thì làm thế nào anh ta có thể chọn lọc các sự thật từ vô số trải nghiệm phức tạp vốn đủ đơn giản để làm lộ ra kết nối của chúng thông qua các quy luật?
-Albert Einstein, Quy nạp và diễn dịch trong vật lí học, Berliner Tageblatt
Chúng tôi đã chỉ ra rằng nếu thuyết tương đối rộng là đúng, thì bất kì mô hình hợp lí nào về vũ trụ cũng phải bắt đầu với một kì dị… Lúc này tôi nghĩ mặc dù có điểm kì dị, nhưng các định luật vật lí vẫn có thể xác định cách Vũ trụ ra đời.
-Stephen Hawking, Lỗ đen và Vũ trụ sơ sinh
Nền tôn giáo tương lai của nhân loại sẽ được xây dựng trên các định luật khoa học.
-Greg Whitefield, trích trong “Nepal trở thành Mecca cho các nghiên cứu Phật giáo”, Kathmandu Post
Các định luật khoa học chỉ là các thuật toán của chương trình này [một mô phỏng thế giới]… Ở cấp độ lượng tử, chúng ta đang nhìn vào ngôn ngữ máy, bên dưới đó có lẽ chính là cái máy, và chẳng có thuật toán nào ở cấp độ ấy, chỉ có các thay đổi trạng thái của cái máy cho phép các thuật toán vận hành. Đây là lí do vì sao các hạt lượng tử trông hành xử quá thất thường và khó tóm bắt – chúng không chính thức “ở trong” mô phỏng; chúng là cái đang làm cho mô phỏng xảy ra.
-James Platt, trò chuyện cá nhân, 1 tháng Ba 2007
Thế nhưng toàn bộ lịch sử khoa học là một câu chuyện rõ ràng về những lí giải liên tục đổi mới và thay đổi của các sự thật cũ. Tuổi thọ của sự trường tồn hình như là hoàn toàn ngẫu nhiên nên nó chẳng nhìn thấy trật tự nào ở chúng cả. Một số chân lí khoa học có vẻ tồn tại hàng thế kỉ, số khác thì kéo dài chưa tới một năm. Chân lí khoa học không phải giáo điều, nó tốt cho đời sau, mà là một thực thể nhất thời định lượng có thể nghiên cứu được như bất kì thứ gì khác.
-Robert Pirsig, Thiền và Nghệ thuật Bảo dưỡng Mô tô
Khoa học hoạt động là do vũ trụ được xếp trật tự theo một cách có thể hiểu được. Hiện thân tinh tế nhất của sự trật tự này được tìm thấy ở các định luật vật lí, các quy tắc toán học cơ bản chi phối mọi hiện tượng thiên nhiên. Một trong những câu hỏi lớn nhất của khoa học đó là nguồn gốc của các định luật đó: do đâu mà có chúng, và tại sao chúng có hình thức như chúng vốn thế?... Các định luật vật lí có một tính chất kì lạ và bất ngờ: cùng với nhau, chúng đem lại cho vũ trụ khả năng tạo ra sự sống và sinh vật có ý thức, ví dụ như chúng ta, những người có thể nêu ra những câu hỏi lớn ấy.
-Paul Davies, “Thiết lập Các Định luật”, New Scientist
Trích từ Archimedes to Hawking (Clifford Pickover)