8.3 Lượng tử hóa vật chất
“Phẩm chất nước đôi” này của ánh sáng còn có những hệ quả cực kì quan trọng và hoàn toàn ngoài trông đợi đối với vật chất. Thật vậy, sự lượng tử hóa của năng lượng điện từ phát ra bởi một nguyên tử hàm ý rằng nội năng của nó cũng phải bị lượng tử hóa! Vì vậy nội năng của nó không thể nhận một giá trị bất kì, mà chỉ nhận những giá trị rạch ròi, chúng phân bố theo một thang bước nhảy cách đều nhau theo tần số photon mà nguyên tử đó có thể phát ra (hay hấp thụ). Điều này đã được các nhà quang phổ học biết rõ vào cuối thế kỉ 19. Ánh sáng phát ra bởi một nguyên tố tinh khiết hóa ra là một hỗn hợp gồm một số lượng hạn chế các tần số rạch ròi. Mỗi nguyên tố hóa học có phổ tần số đặc biệt của riêng nó trong ánh sáng phát ra bởi các nguyên tử của nó, cho nên ta có thể xem quang phổ là chữ kí đặc trưng của nguyên tố. Nhưng điều này có ý nghĩa gì?
Như ta sẽ thấy ở Chương 9, vào cuối thập niên đầu tiên của thế kỉ 20, các nhà khoa học bắt đầu kết luận rằng các nguyên tử là những hệ hỗn hợp gồm một hạt nhân nhỏ khối lượng lớn và tích điện dương, xung quanh là một số electron còn nhỏ hơn nữa, tích điện âm, quay xung quanh hạt nhân, theo kiểu các hành tinh quay xung quanh Mặt Trời. Vì vậy, sự phân bố rời rạc của năng lượng trong quang phổ gợi ý một sự phân bố rời rạc giống như vậy của bán kính (hay hình dạng) của quỹ đạo electron. Nói cách khác, chỉ một số lượng hạn chế quỹ đạo là được phép và chúng tương ứng với moment động lượng quỹ đạo đã biết (xem Chương 2).

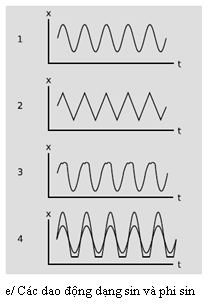
Ta hãy bỏ qua cuộc tranh cãi dai dẳng mà các nhà vật lí thời ấy đã bận tâm về sự lượng tử hóa của moment động lượng, và nhận xét rằng kể cả trong thế giới vĩ mô, với những thứ chúng ta phải đương đầu hằng ngày, chúng ta quan sát thấy những thí dụ đa dạng của “sự lượng tử hóa”. Chẳng hạn, nếu ta gảy một dây đàn ghita, nó sẽ bắt đầu dao động và nửa bước sóng dao động sẽ luôn luôn bằng ước số của tổng chiều dài của dây.4 Đó là một hệ quả rằng chỉ một tập hợp rời rạc các tần số được phép5 bị kích thích. Tương tự, nếu chúng ta gõ vào một xô chứa nước, ta quan sát thấy sóng dừng xuất hiện trên mặt nước, tức là nói chung, khi ta giam cầm một sóng về mặt vật chất, các thông số của nó, ví dụ như bước sóng và tần số, trở nên “bị lượng tử hóa”. Ta sẽ bàn thêm các ví dụ khác của sự lượng tử hóa này ở Chương 9.
Bây giờ ta hãy xét một hiện tượng khác được khám phá thực nghiệm vào năm 1927. Khi bắn một dòng electron đơn năng lượng qua một khe rất hẹp,6 các electron tán xạ phía bên kia vật cản. Hình ảnh các điểm va chạm trên một mặt phẳng trực giao đặt phía bên kia khe không phân bố như người ta trông đợi, tức là với số lượng va chạm giảm dần theo khoảng cách tính từ tâm chiếu của khe ra ngoài, mà nó xuất hiện thành các vân, đúng như bạn trong đợi từ sự nhiễu xạ sóng. Hành trạng này đã được dự đoán bởi nhà vật lí Pháp Louis de Broglie vào năm 1924. Nghiên cứu bản chất nước đôi của photon, de Broglie giả thuyết rằng electron (thật vậy, bất cứ hạt nào) cũng có bản chất nước đôi, tức là biểu hiện các tính chất dạng hạt và dạng sóng. Tương tự như vậy đối với photon, bước sóng “gắn liền” với electron phải tỉ lệ nghịch với động lượng của nó:
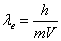
trong đó V là vận tốc của electron so với hệ quy chiếu (quán tính) đã chọn. Ở tốc độ thấp (so với c), tức là trong một gần đúng phi tương đối tính, m là khối lượng nghỉ của electron; ngược lại, nó là khối lượng động m = gmnghỉ, trong đó g là thừa số Lorentz đã giới thiệu ở Chương trước.
Tiếp tục cách làm tương tự như trên, ta tìm được tần số của sóng electron là
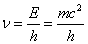
Như vừa đề cập, những cân nhắc này không chỉ hạn chế với electron, mà còn đúng cho bất kì hạt nào. Vì bước sóng tỉ lệ nghịch với khối lượng và các nucleon7 có khối lượng nghỉ lớn hơn electron khoảng 2000 lần, nên bước sóng gắn liền với chúng nhỏ hơn 2000 lần và các hiện tượng nhiễu xạ tương ứng khó quan sát hơn nhiều. Tóm lại, theo giả thuyết de Broglie, vật chất, cũng như ánh sáng (photon), biểu hiện bản chất vừa là hạt vừa là sóng. Sự khác biệt giữa hai bản chất là khối lượng nghỉ của các hạt khác không. Các hạt có các thông số khác giống với photon, ví dụ moment động lượng riêng, gọi là spin, tương tự như spin của con quay.8 Sau một phân tích toán học chi tiết, cái chúng ta bỏ qua ở đây, người ta tìm thấy chỉ có hai giá trị (trị riêng) khả dĩ cho spin của electron và các nucleon. Các giá trị này là: ± h_gạch/2. Nói cách khác, electron và nucleon đều có spin 1/2 (theo đơn vị h_gạch = h/2π).
8.4 Hàm sóng
Sự tương ứng giữa các hạt (vật chất) và photon, do de Broglie đề xuất, đòi hỏi một hàm sóng gắn liền với mỗi đối tượng, để xác định trạng thái sóng của chúng ngoài trạng thái hạt của chúng. Trong trường hợp photon, các sóng có bản chất vật lí rõ ràng là sóng điện từ, ta có thể thu được hình thức rõ ràng của nó bằng cách giải các phương trình Maxwell. Do đó, biên độ của chúng được biểu diễn theo điện trường và từ trường, cái ta có thể đo được. Nhưng đối với các hạt, hàm sóng có ý nghĩa gì và làm thế nào ta có thể đo hay tính được nó?
Thật bất ngờ, câu hỏi thứ ba lại dễ trả lời hơn. Một sóng nói chung được biểu diễn bởi một dạng hàm nào đó, tức là không phải một con số, mà là một hàm ψ (như hàm sóng thường được gọi) của một đối số nào đó. Hàm sóng chứa thông tin về những đại lượng vật lí mà sóng ấy mang. Trong trường hợp sóng điện từ, đối số bao gồm tần số, tỉ lệ với năng lượng của photon đi kèm, và bước sóng, tỉ lệ nghịch với động lượng của chúng.
Chúng ta trông đợi thứ tương tự xảy ra với các hạt; tuy nhiên, vì tốc độ lan truyền là một hằng số chung cho các photon chứ không phải cho các hạt khối lượng lớn, ta cần thêm một ít thông tin và thu được nó từ sự bảo toàn năng lượng mà ta cũng giả định là hợp lệ trong miền đất Lượng tử. Yêu cầu bảo toàn năng lượng đã được giới thiệu qua toán tử Hamilton, cái ta đã gặp ở Chương 4. Bỏ qua các chi tiết toán học, thủ tục này đưa chúng ta đến phương trình Schrödinger, đó là một phương trình vi phân riêng bậc hai (xem Chương 2), nghiệm của nó đem lại hình thức hàm của hàm sóng.
Trở lại với hai câu hỏi đầu, tức là ý nghĩa của ψ và làm thế nào đo nó, câu trả lời thật đáng thất vọng (dù là với các nhà khoa học!). Thật vậy, hóa ra không có ai từng đo được hàm sóng (và rất có khả năng sẽ chẳng có ai đo được) và lí giải thường gặp là ψ chẳng có ý nghĩa gì ngoài việc là một công cụ tính toán để dự đoán kết cục của những phép đo thực tế. Thực chất rành rành ψ chẳng có ý nghĩa vật lí gì! Tranh cãi về điểm này diễn ra kéo dài và kịch liệt và có lẽ sẽ không bao giờ kết thúc, mặc dù các nhà khoa học hầu như đi tới nhất trí chung với nhau về một cách lí giải tối thiểu tiêu chuẩn đã nói ở trên, ít nhất là bởi vì nó hoạt động cực kì tốt. Ở Chương 13, chúng ta sẽ bàn luận nhanh về một cách lí giải khác.
Ta hãy bỏ qua cuộc tranh cãi lịch sử trên và chuyển sang kiến thức được chấp nhận ngày nay. Hàm sóng được xem là một biên độ xác suất, chuẩn của nó bình phương (tức là |ψ| 2) là mật độ xác suất. Nếu ta lấy tích phân |ψ| 2 trên một thể tích đã cho, ta thu được xác suất tìm thấy hạt bên trong thể tích đó. Khái quát hơn, ta có thể sử dụng hàm sóng để ước định xác suất thu được một giá trị cho trước cho năng lượng hay động lượng (hay bất kì tính chất vật lí nào khác) của bất kì hạt nào ở bất kì đâu.
Hàm sóng đánh dấu một khác biệt hết sức to lớn giữa Cơ học Lượng tử và Vật lí Cổ điển. Sự khác biệt ấy có thể được làm rõ với một thí nghiệm Gedanken (thí nghiệm tưởng tượng). Giả sử bạn có một hệ vật chất, với nó bạn biết tất cả các định luật vật lí cố hữu, tất cả các biến và giá trị ban đầu của chúng, và tất cả các điều kiện biên. Trong vật lí cổ điển, một nghiệm của các phương trình tương ứng mang lại một dự đoán chính xác của các kết quả của bất kì thí nghiệm thực nào (ít nhất trên nguyên tắc, bởi vì, trên thực tế, không bao giờ có thể có được kiến thức đầy đủ cần thiết về mọi thứ).
Ngược lại, cái tốt nhất bạn có thể làm trong Cơ học lượng tử, thậm chí trên nguyên tắc, là tính xác suất của kết cục này hay kết cục khác của thí nghiệm của bạn. Trên thực tế, nếu bạn chỉ tiến hành một phép đo, bạn hoàn toàn không thể dự đoán được kết quả. Nếu bạn lặp lại thí nghiệm nhiều lần, thì bạn sẽ thấy các kết quả riêng lẻ nhóm thành một kiểu tương ứng với phân bố xác suất thu được từ hàm sóng. Khả năng dự đoán của Cơ học Lượng tử do đó bị hạn chế với xác suất, giống hệt như trong xổ số, trong đó mua càng nhiều vé số thì xác suất trúng giải của bạn càng cao, nhưng không chắc chắn bạn sẽ trúng (trừ khi bạn mua hết toàn bộ vé số!). Tuy nhiên, có một sự tất định phủ định, vì các phương trình của cơ học lượng tử cho phép bạn nhận ra chắc chắn những kết quả nào không thể là kết cục của thí nghiệm.
Đặc điểm này của cơ học lượng tử chắc chắn gây hoang mang cho chúng ta ngày nay, nhưng nó còn gây hoang mang hơn nữa đối với các nhà vật lí hồi những thập niên đầu của thế kỉ qua. Thật vậy, tham vọng của nền vật lí học khi ấy là dần dần đi tới kiểm soát toàn bộ thực tại vật chất. Mọi thứ được cho là trên nguyên tắc có thể dự báo được, miễn là chúng ta có đủ kiến thức cần thiết. Ngoài ra, Einstein còn cảm thấy hoàn toàn không hài lòng với Cơ học Lượng tử, mặc dù ông đã đóng góp cho sự ra đời của nó. Ông thường nói rằng ông không thể tin nổi Chúa lại chơi xúc xắc để xác định thế giới diễn tiến như thế nào10 và giữ quan điểm rằng phải còn thiếu cái gì đó từ lí thuyết. Ông giữ niềm tin chắc nịch này cho đến cuối đời mình. Tuy nhiên, dường như chẳng có cái gì còn thiếu cả, và Cơ học Lượng tử vận hành tốt đến mức ngày nay đa số các nhà khoa học sống vui vẻ với nó và tránh đặt ra những câu hỏi gây lúng túng. Sự giằng co giữa chủ nghĩa thực dụng và chủ nghĩa bảo thủ luôn gắn liền với sự phát triển của khoa học (cũng như những thành tựu khác của con người).
<< Phần 1 | Phần 3 >>