Tìm hiểu hàm sóng
Phương trình sóng nổi tiếng của Erwin Schrödinger xây dựng trên một cách đặc biệt mô tả chuyển động của một vật trong một trường lực, ví dụ như một hành tinh chuyển động trong trường hấp dẫn của Mặt trời hay một electron chuyển động trong điện trường của một hạt nhân. Trong cả hai trường hợp, trường lực có thể xem là một giếng hình nón với những mặt cong có hình dạng đặc biệt gọi là hyperboloid. Vật có thể xem là một quả cầu đang lăn không ma sát dọc theo thành bên trong của giếng. Không có ma sát, cơ năng toàn phần của vật (thế năng và động năng) được bảo toàn.
Giải các phương trình chuyển động bằng toán học, các nhà vật lí tìm thấy những đường đi được phép nhất định mà vật có thể tuân theo, tùy thuộc vào cơ năng toàn phần của nó. Một vật có khối lượng bất kì, từ một hạt cát nhỏ xíu cho đến một hành tinh khổng lồ, chuyển động dưới tác dụng của lực hấp dẫn của Mặt trời nhưng không đủ năng lượng để thoát ra khỏi hệ mặt trời, sẽ đi theo một quỹ đạo elip. Về mặt toán học, khối lượng được biểu diễn là một hạt với một vị trí và xung lượng xác định tại một thời điểm xác định. Nghiệm thu được cho các phương trình trên là những elip có mọi kích cỡ và độ dẹt. Hình dung dưới dạng một quả cầu đang lăn theo thành cong bên trong của giếng, nó có thể có quỹ đạo tròn nếu nó vẫn duy trì ở một mức đặc biệt. Hoặc nó có thể chuyển động hướng vào trong và hướng ra ngoài trên quỹ đạo elip, chậm dần khi nó leo lên các thành cho đến khi nó đạt tới khoảng cách cực đại của nó, rồi tăng tốc khi nó chuyển động hướng vào trong. Cuối cùng, nó đạt tới một khoảng cách cực tiểu, nơi tốc độ của nó đủ nhanh cho nó trèo ra ngoài trở lại. Các hạt giàu năng lượng hơn chuyển động trong những elip lớn hơn, nhưng mọi hình dạng và độ dẹt của elip, với mọi năng lượng lên tới năng lượng thoát, đều là có thể. (Nếu năng lượng lớn hơn năng lượng thoát, thì nó đi theo một quỹ đạo hyperbol tiến ra xa vô hạn.)
Tuy nhiên, trong thế giới lượng tử, các nhà vật lí đang nhận thấy các electron không thể xem là hạt được. Chúng có thể nằm ngoài khuôn khổ mô tả các vật quay xung quanh Mặt trời có một vị trí và xung lượng xác định vì bước sóng lượng tử, theo công thức de Broglie, nhỏ hơn bản thân vật đến mức khó hình dung ra. (Xung lượng càng lớn thì bước sóng càng nhỏ; cho nên các hành tinh có bước sóng nhỏ hơn nhiều so với các hạt hạ nguyên tử) Nhưng bước sóng electron có thể so sánh với cỡ quỹ đạo của chúng, nghĩa là bản chất sóng của chúng thống trị bên trong nguyên tử. Bằng cách biểu diễn electron là những hàm sóng mờ nhạt thay cho các hạt rõ ràng, phương trình Schrödinger cung cấp cho các nhà vật lí một phương thức xác định các quỹ đạo được phép. Họ nhận thấy chỉ những quỹ đạo và những mức năng lượng nhất định là có thể. Tương ứng với mỗi quỹ đạo là một hàm sóng mô tả electron không phải là một hạt có một xung lượng xác định tại một vị trí xác định mà là một thực thể dạng sóng có một xác suất nhất định đo được trong một vùng cho trước. Tương tự, hàm sóng của electron mang lại một xác suất nhất định của xung lượng của nó trong một vùng nhất định.
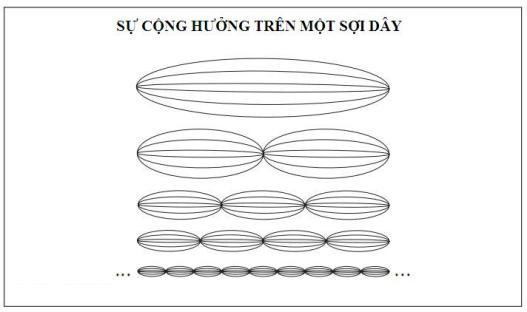
Trong một nguyên tử, các hàm sóng có thể là sóng dừng, giống như nốt của phím đàn organ hoặc dây đàn violin. Electron dạng sóng có thể tìm thấy ở mọi nơi trong vùng quỹ đạo của nó. Trong những trường hợp trung gian, ví dụ như trường hợp thể hiện ở đây, electron vẫn có những tính chất dạng sóng, nhưng cực đại trong hàm sóng khiến người ta có thể xem nó giống một hạt hơn. Cơ hội phát hiện ra electron ở gần cực đại của hàm sóng của nó sẽ lớn hơn, nhưng vẫn có thể tìm thấy nó ở một trong phần đuôi của hàm sóng. Tầm quan trọng của kết quả này sẽ trở nên rõ ràng trong chương 5, 6 và 9.
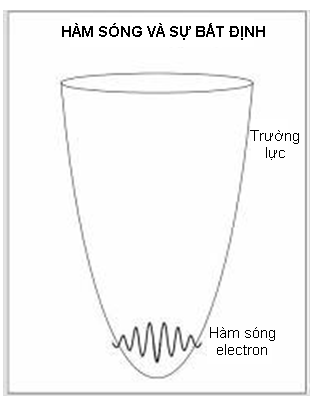
Phương trình Schrödinger mô tả các hạt bằng hàm sóng của chúng, nghĩa là chúng không thể định vị chính xác trong không gian hoặc xung lượng của chúng không thể nào xác định chính xác được. Phép phân tích ma trận của Heisenberg mang lại kết luận tương tự ở dạng nguyên lí bất định.
Lịch sử vật lí thế kỉ 20 - Alfred B. Bortz
Bản dịch của Thuvienvatly.com
<< Phần trước | Phần tiếp theo >>
