Tìm hiểu vũ trụ lượng tử
Mặc dù cơ học lượng tử đã cung cấp một nền tảng lí thuyết, nhưng nhiều nhà vật lí không thể nào chấp nhận bản chất lưỡng tính của electron mà không có sự xác nhận thực nghiệm. Điều đó mất không lâu đã xuất hiện. Những dấu hiệu đầu tiên xuất hiện năm 1926, khi các nhà vật lí người Mĩ Clinton Davisson (1881–1958) và Lester Germer (1896–1971) tìm thấy những kết quả có phần khó hiểu trong một thí nghiệm nghiên cứu cấu trúc tinh thể của nickel. Họ cho phản xạ các electron khỏi bề mặt của một mẩu kim loại và nhận thấy những biến đổi không thể giải thích nổi trong những kết quả của họ. Tại một hội nghị khoa học, Davisson đã mô tả các thí nghiệm của ông với những nhà vật lí khác, và một số người đề xuất rằng có lẽ ông đang trông thấy một hành trạng kiểu sóng. Năm sau đó, Davisson và Germer đã có câu trả lời. Các nguyên tử nickel tạo thành những lớp bên trong tinh thể, và rõ ràng họ đã quan sát thấy hình ảnh giao thoa tạo bởi sự phản xạ các sóng electron từ những lớp khác nhau.
Trong khi đó, nhà vật lí người Anh George P. Thomson (1892–1975), con trai của J.J Thomson nổi tiếng, đang làm thí nghiệm với các chùm electron đi qua những tinh thể rất mỏng. Ông cũng quan sát thấy sự giao thoa. Trong sự kì quặc của lịch sử, Thomson, người có cha đã từng giành giải Nobel vật lí năm 1906 cho việc chứng minh tia ca-tôt không phải là sóng mà là một dòng hạt, giờ lại cùng chia sẻ giải thưởng Nobel năm 1937 với Davisson cho việc phát hiện ra rằng chính những hạt ấy ruốt cuộc lại có tính chất sóng.
Như thường xảy ra trong vật lí lí thuyết, có nhiều hơn một phương pháp toán học để mô tả các hiện tượng lượng tử. Trong khi Schrödinger đang phát triển cơ học sóng của ông, thì một nhà vật lí người Đức khác tên là Werner Heisenberg (1901–76) đã bắt đầu sử dụng một kĩ thuật khác dựa trên các ma trận và vec-tơ. Một ma trận là một sự sắp xếp hàng cột của những con số hay những biểu thức toán học, và vec-tơ là tập hợp những con số hoặc biểu thức sắp xếp trong một hàng hoặc cột. Loại vec-tơ quen thuộc nhất mô tả khoảng cách và hướng từ một điểm trong không gian tới một điểm khác bằng ba con số tương ứng với sự chênh lệch tính theo trục đông-tây, bắc-nam và trên-dưới.
Bất cứ cái gì phương trình Schrödinger tính được thì công thức Heisenberg cũng có thể tính được, nhưng những phương pháp toán học khác nhau mang lại những cái nhìn vật lí khác nhau. Phương pháp Heisenberg không yêu cầu các hạt có bản chất sóng, nhưng nó dẫn tới những kết luận tương tự. Năm 1927, Heisenberg đưa ra một trong những kết luận nổi bật nhất về vũ trụ lượng tử và mang lại tầm quan trọng mới cho hằng số Planck. Nó được gọi là nguyên lí bất định, và nó chỉ dẫn cho các nhà vật lí tiếp tục tiến vào những địa hạt mới, kể cả ngày nay.
Không lâu sau, Heisenberg lưu ý thấy bản chất lượng tử của vũ trụ đặt ra những giới hạn trên cách thức đo chính xác vị trí và xung lượng (hay vận tốc) của một vật. Mọi phép đo vị trí hoặc vận tốc của một vật đều không xác định vì không có thiết bị nào là hoàn hảo, nhưng đó không phải là cái nguyên lí bất định muốn nói. Nguyên lí bất định có nghĩa là có một giới hạn tự nhiên đối với cách thức những đại lượng đó có thể được đo chính xác đồng thời, cho dù thiết bị có được chế tạo tốt bao nhiêu chăng nữa.
Một cách nhìn vào nguyên lí bất định là như thế này: Hoạt động đo ảnh hưởng đến đại lượng đang được đo. Để đo vị trí hoặc xung lượng của một, một thiết bị phải tương tác với vật đó – nghĩa là tác dụng ít nhất là một lực rất nhỏ lên nó. Tương tác đó làm thay đổi cả vị trí và xung lượng của vật, mang lại sai số cho cả hai. Vấn đề đó không thể giải quyết bằng cách làm cho tương tác yếu hơn. Trong khi làm như thế sẽ giảm sai số gây ra bởi tương tác, nhưng nó cũng sẽ tạo ra một tín hiệu yếu hơn, làm tăng sai số của bản thân thiết bị. Một cách khác nghĩ tới nguyên lí bất định là hãy xét xem việc đo đồng thời vị trí và xung lượng của một vật có ý nghĩa gì. Đo xung lượng nghĩa là đo tốc độ mà vị trí của nó đang thay đổi. Để tăng độ chính xác của một thiết bị xác định vị trí của vật, thì thiết bị phải phát hiện ra hạt trong một khoảng thời gian rất ngắn. Một tương tác ngắn đòi hỏi độ nhạy cao hơn, gây ra sai số lớn hơn ở xung lượng đo được của vật. Tương tự, một thiết bị đo xung lượng chính xác hơn đòi hỏi tương tác với vật trong một khoảng thời gian nào đó, vì thế dẫn tới sai số lớn hơn về vị trí của nó.

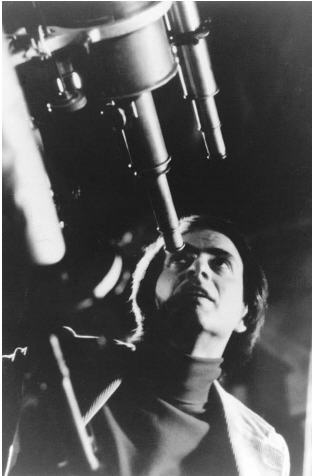
Cách tiếp cận ma trận của Werner Heisenberg với cơ học lượng tử bổ sung cho phương trình Schrödinger và dẫn đến nguyên lí bất định nổi tiếng mang tên ông. (Ảnh: AIP Emilio Segrè Visual Archive)
Heisenberg biểu diễn nguyên lí bất định ở dạng thức toán học, nhưng nó có thể được phát biểu như sau: Độ bất định về vị trí nhân với độ bất định về xung lượng không bao giờ nhỏ hơn hằng số Planck. Đối với một electron trong nguyên tử, độ bất định vị trí của nó tương ứng với cỡ quỹ đạo của nó hay bước sóng của nó, cho nên đối với mọi mục đích thực tiễn, nó có thể được xem là sóng. Việc thử xem electron là một hạt bằng cách đo vị trí của nó chính xác hơn sẽ có một hệ quả kì lạ. Nguyên lí bất định thúc ép một sự bất định lớn về xung lượng của electron đến mức quỹ đạo của nó không thể nào xác định được. Phương pháp Heisenberg không áp đặt lưỡng tính sóng-hạt, nhưng nó có hệ quả tương tự.
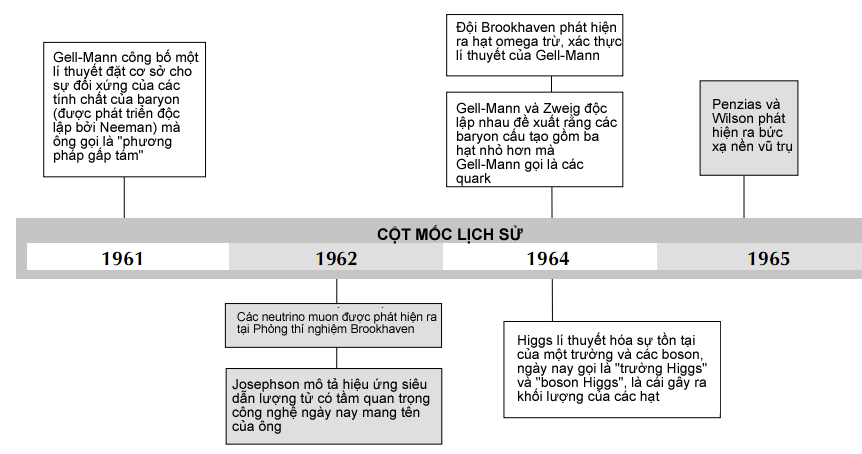
Heisenberg còn nhận ra một mối liên hệ tương tự giữa độ bất định năng lượng của một vật và khoảng thời gian cần thiết để đo năng lượng đó. Sau này, trong thế kỉ 20, các nhà vật lí sẽ sử dụng nguyên lí đó khi họ phát triển các lí thuyết vũ trụ học mô tả nguồn gốc của vũ trụ từ cái rõ ràng chẳng có gì. Nó cũng sẽ chỉ dẫn cho họ trong việc tìm hiểu bản chất của các lực cơ bản liên kết các nguyên tử và hạt nhân lại với nhau. Với công trình này, Heisenberg được trao giải Nobel vật lí năm 1932.
Cơ sở toán học của Heisenberg và Schrödinger còn đưa đến một lời giải thích của nguyên lí loại trừ. Khi các nhà vật lí sử dụng các phương trình trên xác định hàm sóng của những hệ hạt có spin -1/2 giống như các electron trong nguyên tử, thì những nghiệm khả dĩ có thể có không thể nào hơn một electron trong mỗi trạng thái lượng tử. Nguyên lí loại trừ trực tiếp tuân theo phép cộng spin với những bộ số lượng tử cần thiết để mô tả một trạng thái trong một nguyên tử.
Ngoài công trình của họ về thuyết lượng tử vào thập niên 1920, Heisenberg và Pauli còn có những đóng góp quan trọng cho việc tìm hiểu từ tính của vật chất. Công trình của Heisenberg đặc biệt quan trọng đối với việc tìm hiểu hiện tượng sắt từ, hay khả năng của những chất liệu như sắt phát triển từ tính vĩnh cửu. Pauli đã nghiên cứu về sự thuận từ, một tính chất phổ biến của nhiều chất khi đặt trong từ trường. Chúng bị từ hóa tỉ lệ với cường độ của trường ngoài, nhưng từ tính biến mất ngay khi trường không còn nữa.
Cả hai dạng từ tính đó là do spin của electron. Trường ngoài tạo ra một lực có xu hướng sắp thẳng hàng các spin, dẫn tới hành trạng thuận từ. Nhưng trong những liên kết tinh thể nhất định, Heisenberg lưu ý, các cực từ của electron sẽ sắp thẳng hàng với nhau, tạo ra những vùng từ tính vẫn còn tồn tại ngay cả khi trường ngoài tạo ra sự sắp thẳng hàng đã bị loại bỏ. Hiện tượng đó là nguyên nhân của tính sắt từ.
Lịch sử vật lí thế kỉ 20 - Alfred B. Bortz
Bản dịch của Thuvienvatly.com
<< Phần trước | Phần tiếp theo >>