Nghiệm Friedmann, Mật độ tới hạn, và Omega
Nghiệm Friedmann cho EFE có lẽ không được Einstein chú ý tới khi nó được công bố, nhưng nó là trung tâm bàn cãi của số phận của vũ trụ. Việc suy luận ra nghiệm từ EFE nằm ngoài phạm vi của quyển sách này – và tôi cũng không chắc bản thân mình có đủ kiến thức toán để mà làm việc đó – nhưng cái quan trọng là kết quả. Nếu chúng ta giả sử có được nghiệm Friedmann – trong đó, vũ trụ có thể có độ cong dương, âm, hoặc bằng không – thì chẳng còn việc gì nhiều để tìm giá trị cho mật độ tới hạn xác định số phận tối hậu của vũ trụ. Thật vậy, tính toán diễn ra sau đó thật dễ nên giáo viên giảng dạy năm nhất có thể lấy nó làm bài tập ra đề thi.
Friedmann bắt đầu với EFE như Einstein đã viết, bao gồm hằng số vũ trụ.
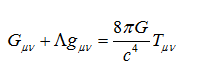
Thực tế μ và ν nhận các giá trị 0, 1, 2 và 3 có thể ví với một bảng phương trình gồm 4 hàng và 4 cột. Friedmann đã giải với phương trình trong bảng phương trình Einstein có m và n đều bằng không. Sau nhiều tính toán theo tôi nghĩ là rất phức tạp, ông đơn giản phương trình này thành như sau
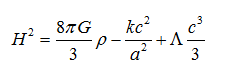
H, G và c là những người bạn cũ: hằng số Hubble, hằng số hấp dẫn, và tốc độ ánh sáng. L là hằng số vũ trụ học, ρ là mật độ trung bình trong toàn vũ trụ, a là một hàm theo thời gian gọi là hệ số tỉ lệ, nhưng ngày nay có thể cho nhận giá trị bằng 1. Friedmann tiếp tục đơn giản bài toán bằng cách giả sử k = 0 (hóa ra đó là cái kinh nghiệm cho thấy), và đồng thời Λ = 0. Phương trình trên đơn giản thành

Phương trình này có thể giải được dễ dàng theo ρ, thu được giá trị ρ = 3H2 / 8πG cho mật độ tới hạn; nếu chúng ta thay những giá trị mới nhất cho G và H, ta thu được một mật độ tới hạn khoảng 5 nguyên tử hydrogen trên mỗi mét khối. Con số này hết sức nhỏ - bất kì ai cũng sẽ nói được rằng lực hấp dẫn được sinh ra sẽ quá nhỏ nên về cơ bản là không tồn tại – tuy nhiên, giá trị đó là đủ lớn rồi. Mật độ này được gọi là mật độ tới hạn – mật độ của vũ trụ là phẳng và không giãn nở - và thường được kí hiệu là ρc.
Omega là tỉ số có tử số là mật độ thực tế và mẫu số là mật độ tới hạn: Ω = ρ / ρc. Vì thế, theo Friedmann, giá trị của Ω sẽ cho chúng ta biết vũ trụ sẽ co lại, xảy ra nếu Ω > 1, hoặc là giãn nở. Điểm mấu chốt là tìm cho được mật độ vật chất của vũ trụ.
Vật chất tối, bức xạ và hằng số vũ trụ học
Có lẽ chúng ta đã ở thời điểm thích hợp để xác định có bao nhiêu vật chất nhìn thấy trong vũ trụ. Các kính thiên văn của chúng ta hoạt động cực kì tốt, và chúng ta có thể phát hiện ra các thiên hà ở xa gần 13 tỉ năm ánh sáng, và chúng ta có thể ngoại suy giá trị mật độ để có chút ý niệm về tổng lượng vật chất nhìn thấy. Như đã lưu ý ở phần trước, chỉ có khoảng 5 nguyên tử hydrogen trong mỗi mét khối, chỉ bằng khoảng 4% khối lượng cần biết để đạt tới mật độ tới hạn.
Tuy nhiên, tổng thể vũ trụ có vẻ được cấu tạo bởi vật chất tối. Kể từ thập niên 1970, bằng chứng bắt đầu tích lũy rằng mỗi thiên hà được vây quanh bởi một quầng vật chất tối. Bằng chứng này dưới dạng vận tốc của những ngôi sao ở xa trong thiên hà đối với khối tâm của thiên hà; những vận tốc này không khớp với giá trị tính được nếu khối lượng trong thiên hà chỉ là cái chúng ta nhìn thấy. Cái chúng ta nhìn thấy không phải là cái chúng ta thu được, chẳng hạn bằng cách đo hấp dẫn. Có nhiều khối lượng trong các thiên hà hơn cái giải thích được chỉ bởi vật chất nhìn thấy.
Có nhiều lí thuyết cho bản chất của vật chất tối. Những lí thuyết này đa dạng từ cái trần tục (vật chất quen thuộc nhưng không bức xạ, giống như những viên đá thực sự tối tăm), cho đến xa lạ (các lí thuyết hạt siêu đối xứng thừa nhận cả một họ vật chất mới chưa ai từng nhìn thấy). Tuy nhiên, đó là chuyện cần lo của các nhà vật lí, còn nhà vũ trụ học (và những ai trong chúng ta nín thở chờ xác định số phận cuối cùng của vũ trụ) chỉ quan tâm nó chứa bao nhiêu thôi. Liệu có đủ vật chất tối để đưa Ω lên quá 1, buộc vũ trụ co lại, hay là không?
Ước tính tốt nhất hiện nay là không có đủ vật chất, dù là sáng, tối hay bất kì cái gì khác, làm được việc đó. Tuy nhiên, mật độ vật chất của vũ trụ chưa phải là toàn bộ vấn đề - còn vấn đề năng lượng nữa. Có rất nhiều bức xạ trong vũ trụ; bức xạ là năng lượng, và thuyết tương đối hẹp Einstein cho chúng ta biết mối liên hệ giữa vật chất và năng lượng là E = mc2, hay m = E / c2. Vì thế, năng lượng cũng phải được tính đến trong omega.
Cuối cùng, hằng số vũ trụ học thật ra chẳng bằng không – theo các phép đo mới nhất thì nó bằng 0,7 – nhưng nó cũng có tác dụng làm tăng mật độ vật chất và năng lượng trong vũ trụ. Kết quả là tỉ số Ω bằng đâu đó giữa 0,98 và 1,1. Con số 1 nằm trong ngưỡng đó, và có lập luận hấp dẫn cho rằng vũ trụ đã được điều chỉnh tinh vi sao cho Ω chính xác bằng 1.
Những con số làm nên vũ trụ
James D. Stein
<< Phần trước | Phần tiếp theo >>