Trong khoa học, trực giác có thể sẽ mang đến cho bạn nhiều rắc rối. Chẳng hạn như lưỡng tính sóng - hạt trong cơ học lượng tử, rồi đến thuyết tương đối dường như bẻ cong mọi suy nghĩ của chúng ta theo cách mà chúng ta không muốn. Tin tưởng vào trực giác của bạn thường sẽ dẫn bạn đến kết luận sai trái. Để minh họa cho điều này, ta xét một số thống kê trong toán học sau đây. Thống kê thường có thể rất lạ. Dưới đây là hai ví dụ minh chứng về những gì tôi nói:
Bài toán về ngày sinh
Cần bao nhiều người trong một căn phòng sao cho có khả năng có hai người cùng ngày sinh, giả sử rằng ngày sinh là một phân bố ngẫu nhiên.
Trả lời theo trực giác (và là trả lời sai):
Nào, hãy nghĩ về chúng một chút. Một năm có 365 ngày. “Có khả năng có hai người cùng ngày sinh”, nghĩa là có 50% cơ hội. Bởi vì ngày sinh là phân bố ngẫu nhiên nên sẽ không có khả năng để lặp lại 2 lần cho đến khi một nửa năm đã trôi qua. Vì vậy sau 182 ngày, người trong phòng tương ứng với số ngày của nửa năm và sẽ có nhiều khả năng hơn nếu có một người nữa bước vào phòng. Vì vậy câu trả lời là 183.
Câu trả lời chính xác là 23. Ngạc nhiên không?
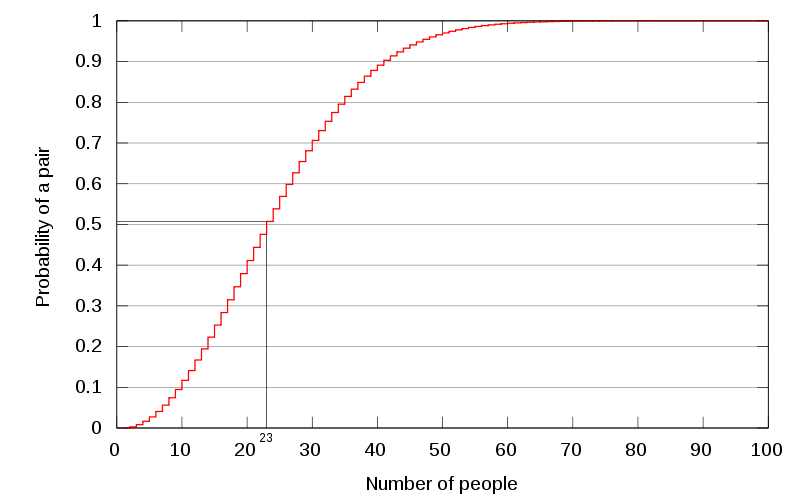
Thậm chí có 23 ngày sinh khác nhau cũng dẫn đến 93,6% những ngày trong năm với 50,7% để có hai người, trong một căn phòng 23 người, có cùng ngày sinh. Đáng ngạc nhiên hơn là nếu có 57 người trong một phòng thì có tới 99% cơ hội để có hai người có cùng ngày sinh. Câu trả lời theo cảm tính ở trên chỉ đúng trong trường hợp câu hỏi là “Có bao nhiêu người trong một phòng sao cho có ít nhất một người cùng ngày sinh với tôi”.
Bài toán về Monty Hall
Máy chủ của trò chơi, Monty Hall, sẽ cho bạn 3 cánh cửa. Phía sau một trong số 3 cánh cửa đó là một chiếc xe hơi mới, sau hai cánh cửa còn lại là một con dê. Bạn chọn một cửa (ví dụ cửa 1). Sau đó Monty sẽ mở cửa số 3 và cho thấy một con dê. Máy chủ sẽ cho bạn một cơ hội - bạn có quyền chọn lại cửa số 2 hoặc vẫn trung thành với lựa chọn ban đầu của mình. Bạn có nên chọn lại không?
Câu trả lời theo cảm tính (và là câu trả lời sai):
Khi chọn lần đầu tôi có 1/3 cơ hội có được chiếc xe hơi. Monty mở một cửa, và nó không phải là xe hơi. Điều đó có nghĩa là xe hơi có thể ở cửa 1 hoặc cửa 2. Cơ hội lúc này là như nhau cho hai cánh cửa nên sẽ không có vấn đề gì với cánh cửa mà tôi đã chọn.
Câu trả lời đúng:
Câu trả lời đúng là nếu thay đổi lựa chọn bạn sẽ tăng từ 1/3 cơ hội lên 2/3 cơ hội. Có một chú ý quan trọng là Monty biết chiếc xe hơi đang ở đâu và sẽ không bao giờ mở cánh cửa có nó (vì sẽ làm hỏng trò chơi). Tôi sẽ chỉ cho bạn lý do toán học tại sao điều này lại đúng. Công cụ thống kê mà chúng ta sử dụng gọi là định lý Bayes, cho phép chúng ta phân tích xác suất của một sự kiện xảy ra khi có một sự kiện khác đã xảy ra rồi. Trong trường hợp này chúng ta cần tính xác suất để có xe hơi ở cửa 1, khi biết có một con cừu ở cửa 3. Định lý Bayes được viết như sau:
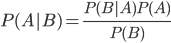
Nghĩa là: Xác suất để xảy ra sự kiện A khi biết sự kiện B thì đúng bằng tích của xác xuất để xảy ra sự kiện B khi biết sự kiện A với xác suất xảy ra sự kiện A chia cho xác suất xảy ra sự kiện B.
Trong bài toán Monty Hall, chúng ta có 3 biến quan trọng. Cửa mà bạn chọn là Dn, cửa mà Monty mở là Mn và cửa thật sự có xe hơi là Cn. Vì vậy xác suất để có xe hơi trong cửa 2 là C2, khi biết bạn chọn D1 và Monty mở cửa M3 là:
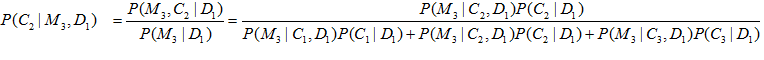
hay:
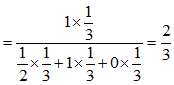
Vì vậy nếu bạn chon cửa 1 và Monty mở cửa 3 thì có 66,6% là chiếc xe hơi ở cửa số 2 và chỉ có 33,3% ở cửa 1. Vì vậy lần tới nếu bạn phải đối mặt với bài toán thống kê trông có vẻ đơn giản, nên nhớ rằng: thống kê cũng thật là ma quái.
Bin Hô dịch
Theo Chad Jones - skeptoid.com