Những con số làm nên vũ trụ - Phần 74

Thuyết tương đối hẹp

Một trong những (trong số nhiều) biểu hiện đầu tiên của tôi khiến tôi đã không là một nhà vật lí tốt là vì tôi gặp rất nhiều khó khăn để hiểu sự giãn nở thời gian và sự co chiều dài, những đặc điểm then chốt của thuyết tương đối hẹp. Tôi từng là một nhà vật lí nhưng tôi chưa từng hiểu những khái niệm vật lí vĩ đại với mức độ rõ ràng như một số khái niệm toán học trọng yếu. Đa số chúng ta cảm thấy bản thân mình chưa hiểu trọn vẹn cái gì đó vào lúc này hay lúc khác; có khi ta loáng thoáng ngỡ như đã hiểu rồi, nhưng sau đó mới biết là không. Thuyết tương đối hẹp Einstein ở trong tình trạng như thế đối với tôi trong suốt năm thập niên kể từ lần đầu tiên tôi gặp nó. Tôi đã đọc nhiều tác phẩm phổ biến kiến thức viết về nó, cũng như nhiều dạng thức toán học đầy đủ trong nhiều loại sách, nhưng tôi chưa hề hiểu nó cho lắm – cho đến khi David McKay đi tới lời giải thích mà tôi sắp trình bày. Đó là lời giải thích đơn giản nhất và dễ hiểu nhất mà tôi biết.

Nếu bạn đã đi xe lửa nhiều lần, có lẽ bạn đã có kinh nghiệm với tình huống sau đây. Có một đoàn tàu trên đường ray kế bên, và qua cửa sổ bạn có thể nhìn thấy những người khác trên đoàn tàu đó. Bất ngờ có sự chuyển động; bạn thấy đoàn tàu kia đang di chuyển. Tuy nhiên, trừ khi có cái gì đó để bạn nhận ra rõ ràng rằng đoàn tàu nào đang di chuyển – ví dụ như một cú giật bất ngờ trên tàu của bạn hay sự chuyển động của những đối tượng cố định hiển nhiên như thanh tà vẹt hay cây cối – bạn không biết được mình đang chuyển động hay bên tàu kia đang chuyển động.

Thuyết tương đối xử lí hai “hệ quy chiếu” – hai đoàn tàu – đang chuyển động ở một vận tốc không đổi so với nhau. Hệ nào thật sự đang chuyển động? Cả hai hệ! Cái then chốt cho cơ sở toán học của thuyết tương đối hẹp là nếu một người ở mỗi đoàn tàu đo cùng một khoảng cách theo mét hoặc cùng một khoảng thời gian theo giây, thì họ sẽ thu về con số giống nhau. Để hiểu được cơ sở hợp lí cho điều này, hãy tưởng tượng trong khi đoàn tàu kia đang ở kế bên tàu của bạn, bạn có hai cái thước mét, và đưa một cái thước cho một người ở đoàn tàu kế bên. Nếu bạn đo cùng một khoảng cách trong thế giới bên ngoài, bạn dùng thước mét của bạn và anh ta dùng thước của anh ta, bạn sẽ thu được con số giống nhau bởi vì câu hỏi ai có cái thước mét thật sự (hay – ai đang chuyển động và ai không) là chuyện gây bàn cãi; không có cách nào nói được bởi vì mỗi bên đều nhìn thấy bên kia đang chuyển động.

Vì thế cái bạn nên làm là: bạn mở cửa sổ và cầm một cái thước mét, một đồng hồ và một đèn flash giống hệt như người dối diện với bạn bên kia. Đó là một cái đèn flash đặc biệt; khi bạn mở đèn lên, nó phát ra một photon độc thân. Hai đoàn tàu chuyển động ra xa nhau ở một vận tốc không đổi, bạn đo vận tốc đó là v m/s; người ở tàu bên kia tính được vận tốc mà bạn đang đi ra xa anh ta cũng là v m/s. Đó là giả thuyết cơ bản của thuyết tương đối – không có người nào trong hai người bạn có thước mét “chính xác” và đồng hồ “chính xác” trong khi người kia có cái “không chính xác”, và vì thế mỗi người phải thu được số đo giống nhau, nếu không một hệ đo bằng cách nào đó lại “chính xác”, còn hệ kia thì không.

Bây giờ giả sử rằng, tại thời điểm người ở trong tàu đi qua bạn, anh ta hướng đèn flash lên trần và bật đèn flash; không bao lâu sau đó thì photon đi tới trần trong tàu của anh ta. Bạn dựng nên một tam giác vuông với ba đỉnh. Đỉnh A là chỗ của bạn tại thời điểm người kia bật đèn flash. Đỉnh C là điểm trên trần tàu lúc photon độc thân đi tới, vì đoàn tàu đã đi được một quãng đường nào đó xuôi theo đường ray từ thời điểm đèn flash bật lên, nên C ở cùng mức cao với trần nhưng lệch theo đường ray. Gọi B là điểm trên đường ray nằm ngay bên dưới C; AC là cạnh huyền của một tam giác vuông. Chúng ta biết theo định lí Pythagoras rằng AC² = AB² + BC².

Quãng đường bằng tốc độ nhân thời gian, và c, vận tốc ánh sáng, có giá trị số như nhau (giống như vận tốc của đoàn tàu) cho dù bạn đo nó hay người ở trong tàu kia đo nó. Bao nhiêu thời gian đã trôi qua giữa thời điểm đèn bật sáng và thời điểm photon đi tới C? Bạn đo quãng đường, nhưng tính thời gian từ phương trình đường đi bằng tốc độ nhân thời gian. Bạn kí hiệu lượng thời gian này là T, và như vậy AC = cT, vì AC là quãng đường photon đã đi; nó bắt đầu tại A và kết thúc tại C. Vì đoàn tàu đang chuyển động ở một vận tốc v không đổi, nên nó bắt đầu tại A và kết thúc tại B, vì thế AB = vT.

Người ở trên tàu kia kí hiệu t là lượng thời gian đã trôi qua giữa thời điểm đèn bật mở và thời điểm chùm sáng đi tới C. Photon đi từ sàn tàu đến trần của nó, quãng đường là BC; người ở trong tàu tính quãng đường đó là ct. Và bạn cũng thế, vì đoạn thẳng AB vuông góc với đoạn thẳng AC, và cả hai thước mét của bạn không bị ảnh hưởng bởi chuyển động theo hướng AB. Chúng ta thay những giá trị này – từ hệ quy chiếu của bạn – vào định lí Pythagoras.

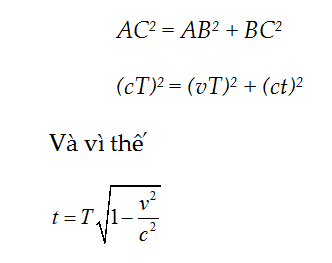
Đây là hiệu ứng “giãn nở thời gian” nổi tiếng; số giây đã trôi qua trên cái đồng hồ của người ở trong tàu kia ít hơn số giây đã trôi qua trên đồng hồ của bạn. Lưu ý rằng chúng ta thậm chí không cần dùng đến đồng hồ; ta thu được thời gian từ công thức quãng đường = vận tốc ´ thời gian.

Nếu chúng ta kí hiệu quãng đường AB mà bạn đo được là L và quãng đường đó do người trong tàu kia đo được là l, ta thấy rằng L = vT và l = vt, vì cả hai bên đều thấy vận tốc của đoàn tàu có giá trị số v bằng nhau. Cho nên v = L / T = l / t, và do đó l = (t / T)L. Thay giá trị thu được trước đó cho t/T ta được