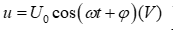Câu hỏi
🗣️ Nguyễn Văn Lộc hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
(A) 2,75μm
(B) −2,25μm
(C) −2,75μm
(D) 2,25μm
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: 30 de thi thu thpt quoc gia mon vat li nam 2022 co loi giai.
Câu trả lời hay nhất
🕵 Bạn Trần Thị Thành trả lời:
Chọn câu (C): −2,75μm
Phương pháp: + Sử dụng biểu thức xác định vị trí trí vân tối: \({x_T} = \left( {k + \frac{1}{2}} \right)i\) + Số vân sáng trong khoảng L bất kì: \( - \frac{L}{i} < k < \frac{L}{i}\) Cách giải: + Tại M và N là 2 vân tối ở hai phía so với vân sáng trung tâm ta suy ra: \(\left\{ {\begin{array}{*{20}{l}}{{x_M} = M\;{{\rm{S}}_1} - M\;{{\rm{S}}_2} = \left( {{k_1} + \frac{1}{2}} \right)i \Rightarrow i = \frac{{{x_M}}}{{{k_1} + \frac{1}{2}}}}\\{{x_N} = N{S_1} - N{S_2} = \left( {{k_2} + \frac{1}{2}} \right)i}\end{array}} \right.\) + Số vân sáng trong khoảng MN thỏa mãn: \(N{S_1} - N\;{{\rm{S}}_2} < ki < M{S_1} - M\;{{\rm{S}}_2} \Leftrightarrow \frac{{{x_N}}}{i} < k < \frac{{{x_M}}}{i} \Leftrightarrow {k_2} + \frac{1}{2} < k < {k_1} + \frac{1}{2}\) Theo đề bài, giữa M và N có 9 vân sáng ⇒ có 9 giá trị của k .
| k1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| k2 | - 9 | -8 | -7 | -6 | -5 | -4 | -3 |
| \({x_N}(\mu m)\) | -29,75 | -8,75 | -4,55 | -2,75 | -1,75 | -1,11 | -0,67 |
|
|
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Trần Thị Đức viết:
Chọn C, −2,75μm
➥ 🗣️ Nguyễn Văn Lộc trả lời: Cảm ơn bạn, câu này hình như có trong file doc này 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải
👤 Nguyễn Thị Dũng viết:
Chọn D, 2,25μm
👤 Nguyễn Thị Thành viết:
Chọn B, −2,25μm
👤 Trần Thị Lộc viết:
Chọn A, 2,75μm
👤 Trần Văn Đại viết:
Chọn C: −2,75μm
Gửi bạn các file hữu ích đi kèm câu hỏi:
- 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
- [Năm 2022] Đề thi thử môn Vật lí THPT Quốc gia có lời giải (30 đề) (.doc)
- [Năm 2022] Đề thi thử môn Vật lý THPT Quốc gia có lời giải (30 đề) (.doc)
- 30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
- 10 đề thi thử tốt nghiệp THPT Quốc gia năm 2021 môn Vật Lí có lời giải chi tiết (.doc)
- 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết (.doc)
- Giao thoa ánh sáng nhiều thành phần đơn sắc
- Câu chuyện phát minh laser: Và thế là có ánh sáng!