Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Trần Hải Huy hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
(A) \(4m/{s^2}\) .
(B) \(2m/{s^2}\) .
(C) \(8m/{s^2}\) .
(D) \(8,3\;{\rm{m}}/{{\rm{s}}^2}\) .
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: 30 de thi thu thpt quoc gia mon vat li nam 2022 co loi giai.
Câu trả lời hay nhất
🕵 Bạn Nguyễn Văn Đông trả lời:
Chọn câu (C): \(8m/{s^2}\) .
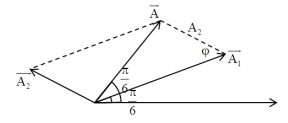
Phương pháp: Sử dụng phương pháp giản đồ vecto Định lí hàm sin: \(\frac{a}{{\sin \hat A}} = \frac{b}{{\sin \hat B}} = \frac{c}{{\sin \hat C}}\) Gia tốc cực đại của dao động điều hòa: \({a_{\max }} = {\omega ^2}A\) Cách giải: Ta có giản đồ vecto: Từ giản đồ vecto, áp dụng định lí hàm sin, ta có: \(\frac{{{A_2}}}{{\sin \frac{\pi }{6}}} = \frac{A}{{\sin \varphi }} \Rightarrow \frac{A}{{\sin \varphi }} = \frac{4}{{\sin \frac{\pi }{6}}} = 8 \Rightarrow A = 8\sin \varphi \) Để độ lớn gia tốc của vật đạt giá trị lớn nhất: \({a_{\max }} \Leftrightarrow {A_{\max }} \Rightarrow {(\sin \varphi )_{\max }} = 1 \Rightarrow {A_{\max }} = 8(\;{\rm{cm}})\) \( \Rightarrow {a_{\max }} = {\omega ^2}{A_{\max }} = {10^2}.8 = 800\left( {\;{\rm{cm}}/{{\rm{s}}^2}} \right) = 8\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\) .
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Nguyễn Văn Thịnh viết:
Chọn C, \(8m/{s^2}\) .
➥ 🗣️ Trần Hải Huy trả lời: Cảm ơn bạn, câu này hình như có trong file doc này 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải
👤 Nguyễn Văn Quân viết:
Chọn D, \(8,3\;{\rm{m}}/{{\rm{s}}^2}\) .
👤 Trần Văn Kiệt viết:
Chọn B, \(2m/{s^2}\) .
👤 Trần Văn Tuấn viết:
Chọn A, \(4m/{s^2}\) .
👤 Lê Phương Phú viết:
Chọn C: \(8m/{s^2}\) .
Gửi bạn các file hữu ích đi kèm câu hỏi:
- 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
- [Năm 2022] Đề thi thử môn Vật lí THPT Quốc gia có lời giải (30 đề) (.doc)
- [Năm 2022] Đề thi thử môn Vật lý THPT Quốc gia có lời giải (30 đề) (.doc)
- 30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
- 10 đề thi thử tốt nghiệp THPT Quốc gia năm 2021 môn Vật Lí có lời giải chi tiết (Phần 2) (.doc)
- 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết (.doc)
- Sơ đồ sự phân bố thời gian chuyển động của vật trên quỹ đạo khi dao động
- Nhà vật lí người Italy Fabiola Gianotti sẽ là nữ tổng giám đốc đầu tiên của CERN
