Thực hiện giao thoa trên bề mặt chất lỏng với hai nguồn kết hợp A, B cách nhau 30cm dao động theo phương thẳng đứng với cùng phương trình \({u_A} = {u_B}

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Lê Hải Thuận hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

(A) 16,00 cm.

(B) 30,30 cm.

(C) 34,00 cm.

(D) 30,07 cm.

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: 30 de thi thu thpt quoc gia mon vat li nam 2022 co loi giai.

Câu trả lời hay nhất

🕵 Bạn Trần Văn Nhật trả lời:

Chọn câu (A): 16,00 cm.

Phương pháp: 

+ Bước sóng: $\lambda \mathrm{ }=\frac{v}{f}$

+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda ;k \in Z\)

Cách giải: 

 

Phương trình dao động của hai nguồn: 

\({u_A} = {u_B} = 5\cos \left( {20\pi t + \frac{{3\pi }}{4}} \right)({\rm{cm}};s)\)

Tốc độ truyền sóng: \(v = 0,2\;{\rm{m}}/{\rm{s}}\)

Bước sóng: $\lambda \mathrm{ }=\frac{v}{f}=2\left(\mathrm{cm}\right)$

Bài cho \(AB = 30\;{\rm{cm}} \Rightarrow {\rm{AB}} = 15\lambda \)

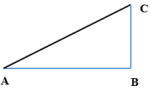
Áp dụng định lí Pitago trong tam giác vuông ABC ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow A{B^2} = A{C^2} - B{C^2}\)

Mà: $\left\{\begin{array}{l}{d}_1=AC\\ d_2=CB\end{array}\right.\Rightarrow d_2^2-d_1^2={(15\lambda )}^2\iff (d_2-d_1)(d_2+d_1)={(15\lambda )}^2$

Mặt khác: \({d_2} - {d_1} = k\lambda \left( 2 \right)\) (cực đại) 

Từ (1) và (2) \( \Rightarrow {d_2} + {d_1} = \frac{{225}}{k}\lambda \)

Để cực đại cùng pha thì k và \(\frac{{225}}{k}\) hoặc cùng chẵn hoặc cùng lẻ, ở đây chỉ có k lẻ thỏa mãn.

Lại có: \({d_2} + {d_1} > 15\lambda \) (tổng hai cạnh bất kì của một tam giác luôn lớn hơn cạnh còn lại)

$\iff \frac{225}{k}\lambda \mathrm{ }>15\lambda \mathrm{ }\Rightarrow k<15$

Lập bảng tìm các giá trị của k thỏa mãn: 

k	1	3	5	9
$\frac{225}{k}$	225	75	45	25

Để gần B nhất thì \({\left( {{d_2} + {d_1}} \right)_{\min }} \Leftrightarrow {\left( {\frac{{225}}{k}\lambda } \right)_{\min }} \Leftrightarrow {k_{\max }} = 9\)

$\Rightarrow \left\{\begin{array}{l}{d}_2-d_1=9\lambda \\ d_2+d_1=\frac{225}{9}\lambda \end{array}\right.\iff \left\{\begin{array}{l}{d}_2=17\lambda \\ d_1=8\lambda =8.2=16\mathrm{cm}\end{array}\right.$

. 

---

Câu trước | Câu kế tiếp

Các câu trả lời

👤 Võ Văn Thành viết:

Chọn C, 34,00 cm.

---

👤 Phan Văn Đức viết:

Chọn D, 30,07 cm.

---

👤 Trương Văn Dũng viết:

Chọn B, 30,30 cm.

---

👤 Bùi Văn Lộc viết:

Chọn A, 16,00 cm.

➥ 🗣️ Lê Hải Thuận trả lời: Cảm ơn bạn, câu này hình như có trong file doc này 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải

---

👤 Nguyễn Phương Dương viết:

Chọn A: 16,00 cm.

Gửi bạn các file hữu ích đi kèm câu hỏi:

• 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
• [Năm 2022] Đề thi thử môn Vật lí THPT Quốc gia có lời giải (30 đề) (.doc)
• [Năm 2022] Đề thi thử môn Vật lý THPT Quốc gia có lời giải (30 đề) (.doc)
• 30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (.doc)
• 10 đề thi thử tốt nghiệp THPT Quốc gia năm 2021 môn Vật Lí có lời giải chi tiết (Phần 2) (.doc)
• 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết (.doc)
• Chuyên đề: Giao thoa sóng với hai nguồn lệch pha nhau
• Ai là người thực hiện thí nghiệm hai khe đầu tiên với electron độc thân?