Một con lắc được treo vào một điểm cố định, đang dao động điều hòa theo phương thẳng đứng. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của độ lớn của

TẢI VỀ (.doc)
Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Trần Nhật Thành hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

Một con lắc được treo vào một điểm cố định, đang dao động điều hòa theo phương thẳng đứng. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của độ lớn của lực kéo về và độ lớn của lực đàn hồi của lò xo tác dụng lên vật theo thời gian. Lấy g = 10 m/s2. Biết t2-t1=7⁢π120⁢s. Tốc độ cực đại của con lắc gần nhất với giá trị nào với giá trị nào
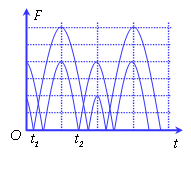
Một con lắc được treo vào một điểm cố định, đang dao động điều (ảnh 1)

(A) 98 cm/s

(B) 85 cm/s

(C) 105 cm/s

(D) 78 cm/s

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: 30 de thi thu thpt quoc gia mon vat li nam 2022 co loi giai.

Câu trả lời hay nhất

🕵 Bạn Nguyễn Hải Dũng trả lời:

Chọn câu (A): 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

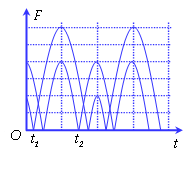
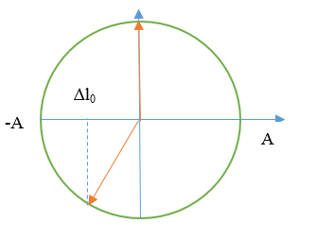
Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Phương pháp : Biểu thức lực đàn hồi: F= - kx biểu thức lực hồi phục:F= - k( x+ ) từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị ta được   theo A Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   tìm được chu kỳ T, , A Cách giải: Biểu thức lực hồi phục và lực đàn hồi : Từ đồ thị thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục, đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị =   =   => =   Thời điểm t1 ứng với vị trí lò xo không giãn Thời điểm t2 ứng với VTCB Sử dụng đường tròn lượng giác từ thời điểm t1   đến t2   Thời gian từ t1 đến t2   là:   = ( arcsin   )   =   = => T=   =>   = 20 rad/s Với   => = 2,5cm => A = 5 cm Tốc độ cực đại : v= = 20.5 = 100 cm/s gần giá trị 98 cm/s

Chỉa sẻ
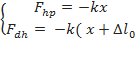
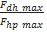
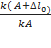
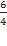
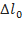
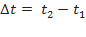
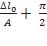
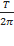
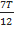
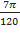
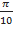
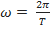
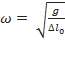
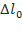
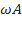
Câu trước | Câu kế tiếp
Các câu trả lời

👤 Đỗ Khánh Đức viết:

Chọn C, 105 cm/s

👤 Trương Văn Lộc viết:

Chọn D, 78 cm/s

👤 Đặng Minh Thành viết:

Chọn B, 85 cm/s

👤 Bùi Anh Phú viết:

Chọn A, 98 cm/s

➥ 🗣️ Trần Nhật Thành trả lời: Cảm ơn bạn, câu này hình như có trong file doc này 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải

👤 Nguyễn Diệp Luân viết:

Chọn A: 98 cm/s

Gửi bạn các file hữu ích đi kèm câu hỏi:

Sách Hackers Toeic Start Reading AL
Sách Hackers Toeic Start Reading AL
Sách Taking The TOEIC Skills and Strategies 1 (QR) First News
Sách Taking The TOEIC Skills and Strategies 1 (QR) First News

Làm thêm Trắc nghiệm ôn thi THPT

Khi nói về lực kéo về trong dao động điều hòa, nhận xét nào dưới đây là đúng ?
Khi nói về lực kéo về trong dao động điều hòa, nhận xét nào dưới đây là đúng ?
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc. Khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc. Khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai
Đặt điện áp xoay chiều u=U0 cos⁡(ωt) (U0 và ω là các hằng số dương) vài hai đầu đoạn mạch chứa điện trở thuần R và tụ điện có điện dung C. Tổng trở của
Đặt điện áp xoay chiều u=U0 cos⁡(ωt) (U0 và ω là các hằng số dương) vài hai đầu đoạn mạch chứa điện trở thuần R và tụ điện có điện dung C. Tổng trở của
Đặt vào hai đầu cuộn sơ cấp của máy biến áp lí tưởng một điện áp xoay chiều có giá trị hiệu dụng không đổi. Nếu quấn thêm vào cuộn thứ cấp 90 vòng thì
Đặt vào hai đầu cuộn sơ cấp của máy biến áp lí tưởng một điện áp xoay chiều có giá trị hiệu dụng không đổi. Nếu quấn thêm vào cuộn thứ cấp 90 vòng thì
Chọn phát biểu đúng. Tại điểm phản xạ cố định thì sóng phản xạ
Chọn phát biểu đúng. Tại điểm phản xạ cố định thì sóng phản xạ
Một ánh sáng đơn sắc truyền trong chân không có bước sóng Lấy h=6,625.10-34Js, c=3.108m/s   Năng lượng của mỗi phôtôn ứng với ánh sáng đơn sắc này
Một ánh sáng đơn sắc truyền trong chân không có bước sóng Lấy h=6,625.10-34Js, c=3.108m/s   Năng lượng của mỗi phôtôn ứng với ánh sáng đơn sắc này