Cho D1, D2 và D3 là ba dao động điều hòa cùng phương, cùng tần số. Dao động tổng hợp của D1 và D2 có phương trình x12=33cosωt+π2 cm. Dao động tổng hợp

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Phạm Ngọc Thành hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

(A) 2,6 cm

(B) 2,7 cm

(C) 3,6 cm

(D) 3,7 cm

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: de thi thu thpt quoc gia mon vat li cuc hay co loi giai chi tiet.

Câu trả lời hay nhất

🕵 Bạn Lê Văn Dũng trả lời:

Chọn câu (A): 2,6 cm

Cách 1:

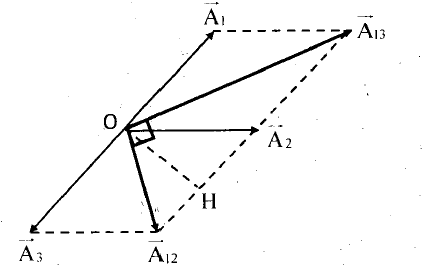
Xây dựng giãn đồ vectơ như hình vẽ.

Ta thấy vectơ $\overrightarrow{A_2}$ đạt giá trị nhỏ nhất khi và chỉ khi vectơ $\overrightarrow{A_2}$ trùng với OH.

Áp dụng hệ thức lượng trong tam giác vuông $\frac{1}{O{H}^2}=\frac{1}{3^2}+\frac{1}{{\left(3\sqrt{3}\right)}^2}\Rightarrow OH=\frac{3\sqrt{3}}{2}cm$

$\Rightarrow A_{2\min }=OH=\frac{3\sqrt{3}}{2}\approx 2,6cm$

Cách 2. Biến đổi đại số.

$\left\{\begin{array}{l}{x}_{12}=x_1+x_2\\ x_{23}=x_2+x_3\\ \frac{x_1}{x_3}=-\frac{A_1}{A_3}\end{array}\right.\Rightarrow \left\{\begin{array}{l}{x}_{12}=x_1+x_2\\ x_{23}=x_2-\underset{x_3}{\underbrace{\frac{A_3}{A_1}{x}_1\Rightarrow }}{x}_2=\frac{x_{23}+\frac{A_3}{A_1}{x}_{12}}{1+\frac{A_3}{A_1}}\end{array}\right.$

(Mục đích của chúng ta là tìm phương trình $x_2$ theo $x_{12}$ và $x_{23}$ bằng cách khử $x_1$ và $x_3$).

Hàm $x_2$ được ghi lại $x_2=\frac{\underset{x_{23}}{\underbrace{3\cos \omega t}}+\frac{A_3}{A_1}.3\sqrt{3}\cos \left(\omega t+\frac{\pi }{2}\right)}{1+\frac{A_3}{A_1}}$

Nhận thấy hai phương trình $x_{23}$ và hàm đóng khung ở biểu thức trên dao động vuông pha với nhau nên biên độ của phương trình $x_2$ có dạng

$A_2=\frac{1}{1+\frac{A_3}{A_1}}\sqrt{3^2+{\left(3\sqrt{3}.\frac{A_3}{A_1}\right)}^2}$; Đặt $\frac{A_3}{A_1}=x>0$.

$$\begin{gathered} \Rightarrow A_2=\frac{1}{1+x}\sqrt{9+27x^2}=\sqrt{\frac{9+27x^2}{{\left(1+x\right)}^2}}=\sqrt{y}\Rightarrow y^{\text{'}}=\frac{54x^2+36x-18}{{\left(1+x\right)}^4}=0\Rightarrow x_0=\frac{1}{3} \\ \Rightarrow A_2=\sqrt{y}=\sqrt{\frac{9+27.{\left(3^{-1}\right)}^2}{{\left(1+3^{-1}\right)}^2}}=1,5\sqrt{3}cm\approx 2,6cm \end{gathered}$$

Chú ý: Có thể tìm cực trị (cũng là giá trị cực tiểu) hàm $A_2=\sqrt{\frac{9+27x^2}{{\left(1+x\right)}^2}}$ bằng máy tính cầm tay FX-570VN.

Các giá trị Start và End ra dựa vào số liệu

$\left\{\begin{array}{l}{A}_{12}=3\sqrt{3}cm\\ A_{23}=3cm\end{array}\right.\Rightarrow \frac{A_{12}}{A_{13}}=\sqrt{3}\approx 1,73A_{23}=3$ thì tỉ số $X=\frac{A_3}{A_1}$ cũng sẽ nằm cỡ vào trong các khoảng từ 1 đến 10 nếu ($A_3>A_1$) còn nếu ($A_3<A_1$) thì tỉ số $X\in \left(0;1\right)$. Bấm Mode 7 và nhập hàm $F\left(X\right)=\sqrt{\frac{27+9x^2}{{\left(1+x\right)}^2}}$

$\left\{\begin{array}{l}Start=1\\ End=10\end{array}\right.\stackrel{\frac{End-Start}{Step}+1\le 30}{\to }Step\ge 0,31\Rightarrow Step=0,4$ (Không tìm được cực trị).

Ta ại $\left\{\begin{array}{l}Start=0,1\\ End=1\end{array}\right.\stackrel{\frac{End-Start}{Step}+1\le 30}{\to }Step\ge 0,031\Rightarrow Step=0,04$

Màn hình hiển thị ở dưới.

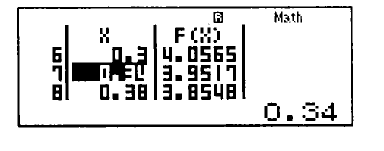
Chú ý:

Trong toán học khi bài toán yêu cầu tìm cực trị thì các em đạo hàm của hàm y sau đó xét $y\text{'}=0$ và lập bảng biến thiên để xét giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN). Tuy nhiên thông thường đối với bài toán vật lí hàm y có nghĩa khi nghiệm đó là nghiệm dương, khi đó đề hỏi GTLN hoặc GTNN thì khi đạo hàm của hàm y thì chỉ có duy nhất 1 nghiệm dương (tức là tồn tại GTLN thì không tồn tại GTNN và ngược lại). Dó đó chúng ta không cần vẽ bảng biến thiên mà kết luận ngay tại giá trị $x_0$ nào đó ($x_0$ là nghiệm dương duy nhất của hàm $y\text{'}$) hàm đạt GTLN (GTNN).

---

Câu trước | Câu kế tiếp

Các câu trả lời

👤 Nguyễn Văn Đức viết:

Chọn C, 3,6 cm

---

👤 Trần Văn Dũng viết:

Chọn D, 3,7 cm

---

👤 Trần Văn Thành viết:

Chọn B, 2,7 cm

---

👤 Nguyễn Văn Phú viết:

Chọn A, 2,6 cm

➥ 🗣️ Phạm Ngọc Thành trả lời: Cảm ơn bạn, câu này hình như có trong file doc này 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết

---

👤 Trần Văn Trường viết:

Chọn A: 2,6 cm

Gửi bạn các file hữu ích đi kèm câu hỏi:

• 30 Đề thi thử thpt quốc gia môn Vật Lí 2020 cực hay nói lời giải chi tiết (.doc)
• Bộ đề thi thử thpt quốc gia môn Vật Lý cực hay có lời giải chi tiết (.doc)
• 20 Đề luyện thi thpt quốc gia môn Vật Lí cực hay có lời giải chi tiết (.doc)
• 5 Đề thi thử thpt quốc gia môn Vật lí cực hay có lời giải (.doc)
• 20 Bộ đề thi thử thpt quốc gia môn Vật Lí cực hay có lời giải (.doc)
• Đề thi thử thpt quốc gia môn Vật Lí mới nhất có lời giải chi tiết (.doc)
• NÂNG CẤP MÁY CASIO FX-500MS THÀNH FX-570MS ĐỂ GIẢI BÀI TOÁN TỔNG HỢP DAO ĐỘNG
• Bài giảng Dao động và Sóng (Phần 12)