Câu hỏi
🗣️ Huỳnh Thị Trí hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
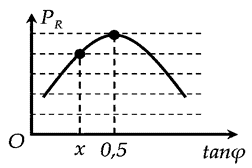
Đặt điện áp \(u = U\sqrt 2 {\rm{cos}}\omega t\) (U; \(\omega \) không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm biến trở \(R\), cuộn dây không thuần cảm và tụ điện. Gọi \(\varphi \) là độ lệch pha giữa hai đầu đoạn mạch và cường độ dòng điện trong mạch; \({P_R}\) là công suất tỏa nhiệt trên \(R\). Hình vẽ bên là một phần đồ thị biểu diễn mối liên hệ giữa \({P_R}\) và \({\rm{tan}}\varphi \). Giá trị của \(x\) bằng
(A) 0,268
(B) 0,273
(C) 0,246
(D) 0,292
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li so gd vinh phuc co dap an.
Câu trả lời hay nhất
🕵 Bạn Trần Thị Đạt trả lời:
Chọn câu (A): 0,268
\({P_{R\max }} \Leftrightarrow {R_0} = {Z_{rLC}} = 1\) (chuẩn hóa) \( \Rightarrow {r^2} + Z_{LC}^2 = 1\) (1) Ta có \(\tan {\varphi _0} = \frac{{{Z_{LC}}}}{{{R_0} + r}} \Rightarrow 0,5 = \frac{{{Z_{LC}}}}{{1 + r}}\) (2) Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}r = 0,6\\{Z_{LC}} = 0,8\end{array} \right.\) Khi \({P_R} = \frac{4}{5}{P_{R\max }} \Rightarrow \frac{{{U^2}R}}{{{{\left( {R + r} \right)}^2} + Z_{LC}^2}} = \frac{4}{5}\frac{{{U^2}{R_0}}}{{{{\left( {{R_0} + r} \right)}^2} + Z_{LC}^2}}\) \( \Rightarrow \frac{R}{{{{\left( {R + 0,6} \right)}^2} + 0,{8^2}}} = \frac{4}{5}\frac{1}{{{{\left( {1 + 0,6} \right)}^2} + 0,{8^2}}} \Rightarrow R \approx 2,38\) Vậy \(x = \frac{{{Z_{LC}}}}{{R + r}} = \frac{{0,8}}{{2,38 + 0,6}} \approx 0,268\) .
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Trần Thị Danh viết:
Chọn C, 0,246
👤 Nguyễn Thị Kiên viết:
Chọn D, 0,292
👤 Nguyễn Thị Trường viết:
Chọn B, 0,273
👤 Trần Thị Bình viết:
Chọn A, 0,268
➥ 🗣️ Huỳnh Thị Trí trả lời: Cảm ơn bạn, câu này hình như có trong file pdf này Đề và đáp án thi HSG Vật lí 12 chuyên Vĩnh Phúc 2013
👤 Trần Văn Tài viết:
Chọn A: 0,268
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Đề và đáp án thi HSG Vật lí 12 chuyên Vĩnh Phúc 2013 (.pdf)
- ĐÁP ÁN CHI TIẾT MÔN VẬT LÝ MÃ 357 THI THỬ ĐH VĨNH PHÚC LẦN 2 NĂM 2013 (.doc)
- File word đề thi thử môn vật lí lần 2 2015- Đại học Vinh (có bài giải đính kèm) (.rar)
- Đề, đáp án HSG lí 11 Vĩnh Phúc 2012-2013 (.doc)
- Đáp án chi tiết Đề thi thử đại học môn Vật lí trường THPT chuyên- Đại học Vinh năm 2015 (.pdf)
- Đáp án đề khảo sát ĐH lần 4 _ Chuyên Vĩnh Phúc (.doc)
- Nguồn gốc của từ trường có thể nằm ở các biến dạng không thời gian của thuyết tương đối đặc biệt
- Những người hoài nghi sự biến đổi khí hậu là những nhà khoa học ‘không đáng tin’
![Trên một sợi dây đàn hồi OC đang có sóng dừng ổn định với bước sóng λ, chu kỳ T. Hình ảnh sợi dây tại thời điểm t (nét đứt) và thời điểm \[t + \frac{T}{4}\]](/images/cau-hoi-3/tren-mot-soi-day-dan-hoi-oc-dang-co-song-dung-on-dinh-0-54298.png)
