Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
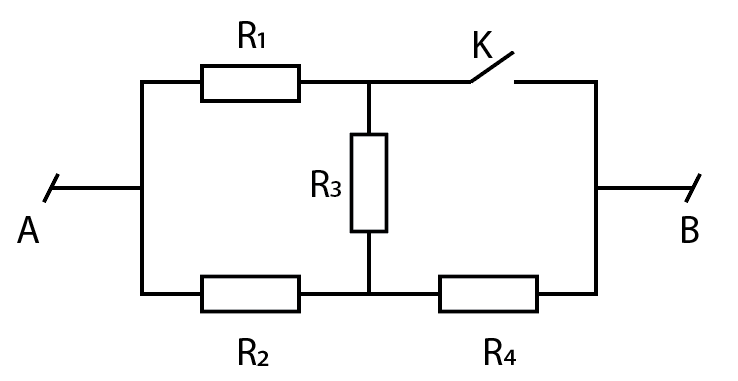
🗣️ Trần Văn Lộc hỏi: Cho mình hỏi một câu Trắc nghiệm Vật Lý lớp 12 trong sách bài tập
Cho mạch điện như hình vẽ, biết R1 = R3 = 45 Ω, R2 = 90 Ω, U = 90 V. Khi khóa K mở hoặc đóng thì cường độ dòng điện qua R4 không đổi. Tính R4, U4.
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: trac nghiem tong hop vat li 2023 co dap an.
Câu trả lời hay nhất
🕵 Bạn Phạm Thị Thành trả lời:
Lời giải: + Khi K mở ta có sơ đồ: \[{R_{13}} = {R_1} + {R_3} = 45 + 45 = 90\Omega \] \[{R_{123}} = \frac{{{R_{13}}.{R_2}}}{{{R_{13}} + {R_2}}} = \frac{{90.90}}{{90 + 90}} = 45\Omega \] Điện trở tương đương toàn mạch là: \[R = {R_{123}} + {R_4} = 45 + {R_4}\] Cường độ dòng điện qua \[{R_4}\]khi K mở là: \[{I_4} = \frac{U}{R} = \frac{{90}}{{45 + {R_4}}}\] + Khi K đóng ta có sơ đồ: \[{R_{34}}\prime = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\] \[{R_{234}}\prime = {R_2} + {R_{34}}\prime = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\] Ta có: \[{U_{234}}' = U = 90V\] \[ \Rightarrow {I_{234}}' = {I_2}' = {I_{34}}' = \frac{U}{{{R_{234}}}} = \frac{{90\left( {45 + {R_4}} \right)}}{{4050 + 135{R_4}}} = \frac{{4050 + 90{R_4}}}{{4050 + 135{R_4}}}\] \[ \Rightarrow {U_2}^' = {I_2}^'{R_2} = \frac{{\left( {4050 + 90{R_4}} \right).90}}{{4050 + 135{R_4}}} = \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\] \[ = > {U_4}' = {U_{34}}' = {U_{234}}' - {U_2}' = 90 - \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\] \[ = \frac{{364500 + 12150{R_4} - 364500 - 8100{R_4}}}{{4050 + 135{R_4}}} = \frac{{4050{R_4}}}{{4050 + 135{R_4}}}\] \[ \Rightarrow {I_4}^' = \frac{{{U_4}^'}}{{{R_4}}} = \frac{{4050{R_4}}}{{{R_4}\left( {4050 + 135{R_4}} \right)}} = \frac{{4050}}{{4050 + 135{R_4}}}\] Từ hai trường hợp K đóng và K mở trên suy ra: \[{I_4} = {I_4}^' \Leftrightarrow \frac{{4050}}{{4050 + 135{R_4}}} = \frac{{90}}{{45 + {R_4}}}\] \[ \Rightarrow 4050\left( {45 + {R_4}} \right) = 90\left( {4050 + 135{R_4}} \right)\] \[ \Rightarrow {R_4} = - 22,5\,\Omega \] (loại). Không có giá trị của R4 thoả mãn điều kiện bài toán.
![Lời giải:
+ Khi K mở ta có sơ đồ:
\[{R_{13}} = {R_1} + {R_3} = 45 + 45 = 90\Omega \]
\[{R_{123}} = \frac{{{R_{13}}.{R_2}}}{{{R_{13}} + {R_2}}} = \frac{{90.90}}{{90 + 90}} = 45\Omega \]
Điện trở tương đương toàn mạch là: \[R = {R_{123}} + {R_4} = 45 + {R_4}\]
Cường độ dòng điện qua \[{R_4}\]khi K mở là: \[{I_4} = \frac{U}{R} = \frac{{90}}{{45 + {R_4}}}\]
+ Khi K đóng ta có sơ đồ:
\[{R_{34}}\prime = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\]
\[{R_{234}}\prime = {R_2} + {R_{34}}\prime = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\]
Ta có: \[{U_{234}}](/images/cau-hoi/tra-loi-cho-mach-dien-nhu-hinh-ve-biet-r1-r3-45-r2-0-7759.png)
{U_4}' = {U_{34}}' = {U_{234}}' - {U_2}' = 90 - \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\] \[ = \frac{{364500 + 12150{R_4} - 364500 - 8100{R_4}}}{{4050 + 135{R_4}}} = \frac{{4050{R_4}}}{{4050 + 135{R_4}}}\]
\[ \Rightarrow {I_4}^' = \frac{{{U_4}^'}}{{{R_4}}} = \frac{{4050{R_4}}}{{{R_4}\left( {4050 + 135{R_4}} \right)}} = \frac{{4050}}{{4050 + 135{R_4}}}\]
Từ hai trường hợp K đóng và K mở trên suy ra:
\[{I_4} = {I_4}^' \Leftrightarrow \frac{{4050}}{{4050 + 135{R_4}}} = \frac{{90}}{{45 + {R_4}}}\]
\[ \Rightarrow 4050\left( {45 + {R_4}} \right) = 90\left( {4050 + 135{R_4}} \right)\]
\[ \Rightarrow {R_4} = - 22,5\,\Omega \] (loại). Không có giá trị của R4 thoả mãn điều kiện bài toán.' class='img-fluid'>
![Lời giải:
+ Khi K mở ta có sơ đồ:
\[{R_{13}} = {R_1} + {R_3} = 45 + 45 = 90\Omega \]
\[{R_{123}} = \frac{{{R_{13}}.{R_2}}}{{{R_{13}} + {R_2}}} = \frac{{90.90}}{{90 + 90}} = 45\Omega \]
Điện trở tương đương toàn mạch là: \[R = {R_{123}} + {R_4} = 45 + {R_4}\]
Cường độ dòng điện qua \[{R_4}\]khi K mở là: \[{I_4} = \frac{U}{R} = \frac{{90}}{{45 + {R_4}}}\]
+ Khi K đóng ta có sơ đồ:
\[{R_{34}}\prime = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\]
\[{R_{234}}\prime = {R_2} + {R_{34}}\prime = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\]
Ta có: \[{U_{234}}](/images/cau-hoi/tra-loi-cho-mach-dien-nhu-hinh-ve-biet-r1-r3-45-r2-1-7598.png)
{U_4}' = {U_{34}}' = {U_{234}}' - {U_2}' = 90 - \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\] \[ = \frac{{364500 + 12150{R_4} - 364500 - 8100{R_4}}}{{4050 + 135{R_4}}} = \frac{{4050{R_4}}}{{4050 + 135{R_4}}}\]
\[ \Rightarrow {I_4}^' = \frac{{{U_4}^'}}{{{R_4}}} = \frac{{4050{R_4}}}{{{R_4}\left( {4050 + 135{R_4}} \right)}} = \frac{{4050}}{{4050 + 135{R_4}}}\]
Từ hai trường hợp K đóng và K mở trên suy ra:
\[{I_4} = {I_4}^' \Leftrightarrow \frac{{4050}}{{4050 + 135{R_4}}} = \frac{{90}}{{45 + {R_4}}}\]
\[ \Rightarrow 4050\left( {45 + {R_4}} \right) = 90\left( {4050 + 135{R_4}} \right)\]
\[ \Rightarrow {R_4} = - 22,5\,\Omega \] (loại). Không có giá trị của R4 thoả mãn điều kiện bài toán.' class='img-fluid'>
Câu trước | Câu kế tiếp
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp lực – Phân tích lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 5. Tổng hợp và phân tích lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp và phân tích lực. Cân bằng lực có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 5: Chuyển động tổng hợp (Phần 2) có đáp án (.doc)
- Trắc nghiệm Vật lí 10 Bài 2: Đồ thị độ dịch chuyển theo thời gian. Độ dịch chuyển tổng hợp và vận tốc tổng hợp có đáp án (.doc)
- Dòng điện làm cho các thiết bị hoạt động như thế nào?
- Tàu Hayabusa đã trở về... nhưng có bụi tiểu hành tinh hay không thì phải chờ xem
![[SÁCH MỚI] Đột Phá 8+ Môn Vật Lí Tập 2 Classic Ôn Thi Đại Học - THPT Quốc Gia Siêu Tiết Kiệm](https://thuvienvatly.com/images/deals/thumb/sach-moi-dot-pha-8-mon-vat-li-tap-2-classic-on-thi-dai-hoc-thpt-quoc-gia-sieu-tiet-kiem.jpg)
