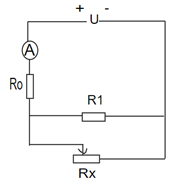
Cho mạch điện: U = 16V , R0 =4 Ω , R1 = 12 Ω, Rx là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.. . 1. Tính

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Lê Thị Anh hỏi: Cho mình hỏi một câu Trắc nghiệm Vật Lý lớp 12 trong sách bài tập

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: trac nghiem tong hop vat li 2023 co dap an.

Câu trả lời hay nhất

🕵 Bạn Trần Ngọc Ngọc trả lời:

Lời giải Mạch: \({R_0}nt\left( {{R_1}//R{}_x} \right)\) Đặt Rx = x \(\left( \Omega \right)\) \({R_{td}} = {R_0} + \frac{{{R_1}.x}}{{{R_1} + x}} = 4 + \frac{{12x}}{{12 + x}} = \frac{{16x + 48}}{{12 + x}}\) \( \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{16}}{{\frac{{16x + 48}}{{12 + x}}}} = \frac{{12 + x}}{{x + 3}}\) \({U_{Rx}} = U{}_{R1} = U{}_{R1x} = \frac{{12 + x}}{{x + 3}}.\frac{{12x}}{{12 + x}} = \frac{{12x}}{{x + 3}}\) Mà \(P = \frac{{U_{Rx}^2}}{{{R_x}}} = 9W \Leftrightarrow \frac{{\frac{{144{x^2}}}{{{{\left( {x + 3} \right)}^2}}}}}{x} = 9 \Rightarrow 9{x^2} - 90x + 81 = 0\) \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow {R_x} = 1\left( \Omega \right)}\\{x = 9 \Rightarrow {R_x} = 9\left( \Omega \right)}\end{array}} \right.\) Hiệu suất của mạch điện \(H = \frac{{{P_{1x}}}}{P}.100\% = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.{R_{td}}}}.100\% = \frac{{{R_{1x}}}}{{{R_{td}}}}.100\% = \frac{{3{R_x}}}{{4{R_x} + 12}}.100\% \) + Rx = 1\(\left( \Omega \right)\) \( \Rightarrow H = 18,75\% \) + Rx = 9\(\left( \Omega \right)\) \( \Rightarrow H = 56,25\% \) b. Từ câu a \( \Rightarrow {P_{{R_x}}} = \frac{{{U^2}}}{{{R_x}}} = \frac{{{{\left( {\frac{{12x}}{{x + 3}}} \right)}^2}}}{x} = \frac{{144x}}{{{x^2} + 6x + 9}} = \frac{{144}}{{x + \frac{9}{x} + 6}}\) Để PRx max khi \((x + \frac{9}{x} + 6)\,\,\min \)\( \Rightarrow \left( {x + \frac{9}{x}} \right)\,\,\min \) Áp dụng BĐT Cô – si: \(x + \frac{9}{x} \ge 2\sqrt {x.\frac{9}{x}} = 6\) \( \Rightarrow {P_{Rx\,max}} = \frac{{144}}{{6 + 6}} = 12\,\left( W \right)\)

---

Câu trước | Câu kế tiếp

Gửi bạn các file hữu ích đi kèm câu hỏi:

• Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (.doc)
• Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp lực – Phân tích lực có đáp án (.doc)
• Trắc nghiệm Vật lí 10 Bài 5. Tổng hợp và phân tích lực có đáp án (.doc)
• Trắc nghiệm Vật lí 10 Bài 13. Tổng hợp và phân tích lực. Cân bằng lực có đáp án (.doc)
• Trắc nghiệm Vật lí 10 Bài 5: Chuyển động tổng hợp (Phần 2) có đáp án (.doc)
• Trắc nghiệm Vật lí 10 Bài 2: Đồ thị độ dịch chuyển theo thời gian. Độ dịch chuyển tổng hợp và vận tốc tổng hợp có đáp án (.doc)
• Tính điện trở của đoạn mạch phân nhánh
• Tính chất điện của dây nano là do các electron quyết định