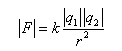Benjamin Crowell
5.2 Trường hấp dẫn
Cho rằng các trường lực là có thực, vậy làm thế nào chúng ta định nghĩa, đo lường và tính toán chúng ? Một phép ẩn dụ dễ hình dung là giống như gió thổi mà con tàu biển phải chịu. Cho dù là con tàu tiến về phía nào, nó sẽ cảm nhận một lượng lực nhất định từ ngọn gió, và lực đó sẽ ở vào một hướng nhất định. Tất nhiên thời tiết luôn luôn biến đổi, nhưng bây giờ hãy chỉ tưởng tượng đến hình ảnh ngọn gió ổn định thôi. Các định nghĩa trong vật lí học là có tính hành động, tức là chúng mô tả làm thế nào đo được thứ đã định nghĩa. Thuyền trưởng của con tàu có thể đo “trường lực” của ngọn gió bằng cách tiến tới vị trí thấy thích và xác định cả hướng gió lẫn cường độ mà nó đang thổi. Lập đồ thị tất cả những phép đo này trên một bản vẽ đưa đến một sự miêu tả của trường lực gió giống như trong hình minh họa. Đây là phương pháp “biển vectơ” của việc hình dung trường.
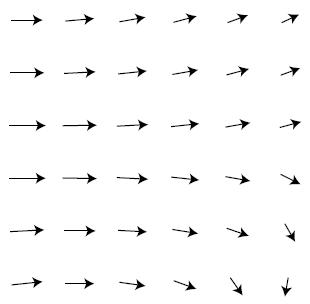
f/ Hình ảnh gió trên một khu vực nhất định của đại dương có thể lập biểu đồ theo phương pháp “biển vectơ” như thế này. Mỗi mũi tên biểu diễn cho cả cường độ gió và hướng của nó tại một nơi nhất định.
Bây giờ hãy xem làm thế nào những khái niệm này áp dụng được cho các trường lực cơ bản của vũ trụ. Chúng ta bắt đầu với trường hấp dẫn, đó là đối tượng dễ hiểu nhất. Như đối với hình ảnh gió thổi, chúng ta bắt đầu bằng việc tưởng tượng hấp dẫn là một trường tĩnh, mặc dù sự tồn tại của thủy triều chứng tỏ có sự thay đổi liên tục ở trường hấp dẫn trong vùng không gian của chúng ta. Việc định nghĩa hướng của trường hấp dẫn khá dễ: chúng ta chỉ đơn giản tiến đến vị trí thấy thích và đo hướng của lực hấp dẫn tác dụng lên vật, ví dụ như một quả nặng buộc vào đầu một sợi dây.
Nhưng làm thế nào chúng ta định nghĩa được cường độ của lực hấp dẫn ? Lực hấp dẫn trên mặt trăng yếu hơn nhiều so với trên Trái Đất, nhưng không thể nào định rõ một cách đơn giản cường độ hấp dẫn bằng cách cho đại một số newton nhất định. Số newton của lực hấp dẫn không những phụ thuộc vào cường độ trường hấp dẫn địa phương mà còn phụ thuộc vào khối lượng của vật mà chúng ta kiểm tra sự hấp dẫn, tức “khối lượng thử” của chúng ta. Một tảng đá trên mặt trăng cảm nhận lực hấp dẫn mạnh hơn một hòn sỏi trên Trái Đất. Chúng ta có thể giải quyết vấn đề này bằng cách định nghĩa cường độ của trường hấp dẫn là lực tác dụng lên một vật, chia cho khối lượng của vật đó.
định nghĩa trường hấp dẫn
Vectơ trường hấp dẫn, g, ở bất kì vị trí nào trong không gian được xác định bằng cách đặt một khối lượng thử mt tại điểm đó. Vectơ trường khi đó được xác định bởi g = F/mt, trong đó F là lực hấp dẫn tác dụng lên khối lượng thử.
Độ lớn của trường hấp dẫn ở gần bề mặt Trái Đất vào khoảng 9,8 N/kg và không phải là sự trùng hợp ngẫu nhiên mà con số này trông quen thuộc, hay kí hiệu g là giống hệt như kí hiệu cho gia tốc trọng trường. Lực hấp dẫn tác dụng lên khối lượng thử sẽ bằng mtg, trong đó g là gia tốc trọng trường. Vậy tại sao lại định nghĩa một tên gọi mới và đơn vị mới cho cùng một đại lượng cũ ? Lí do chủ yếu là nó dọn đường cho chúng ta tiếp cận việc định nghĩa các trường khác.
Điều tinh tế nhất ở đây là trường hấp dẫn sẽ cho chúng ta biết lực gì sẽ tác dụng lên một khối lượng thử bởi Trái Đất, Mặt Trời, Mặt Trăng và toàn bộ phần còn lại của vũ trụ, nếu chúng ta xen một khối lượng thử vào điểm khảo sát. Trường hấp dẫn vẫn tồn tại ở mọi nơi mà chúng ta không đo nó.
Ví dụ 1. Trường hấp dẫn của Trái Đất
Độ lớn của trường hấp dẫn của Trái Đất, theo khối lượng M của nó và khoảng cách r tính từ tâm của nó, bằng bao nhiêu ?
Thay |F| = GMmt/r2 vào định nghĩa trường hấp dẫn, chúng ta tìm được |g| = GM/r2. Biểu thức này có thể dùng cho trường hấp dẫn của bất kì sự phân bố khối lượng đối xứng cầu nào khác, vì phương trình chúng ta thừa nhận cho lực hấp dẫn áp dụng được cho những trường hợp như thế.
Nguồn và bồn
Nếu chúng ta thực hiện một bức tranh biển-mũi-tên của trường hấp dẫn xung quanh Trái Đất, g, kết quả làm liên tưởng đến hình ảnh nước chảy xuống một cái rãnh. Vì lí do này mà bất cứ thứ gì tạo ra một trường ở xung quanh hướng vào bên trong nó được gọi là bồn. Trái Đất là một bồn hấp dẫn. Thuật ngữ “nguồn” có thể chỉ riêng những thứ tạo ra một trường hướng xa ra bên ngoài, hoặc nó có thể được dùng làm thuật ngữ khái quát hơn cho cả trường hợp “hướng ra” và “hướng vào”. Tuy lộn xộn thuật ngữ, nhưng chúng ta biết rằng trường hấp dẫn chỉ có tính hút, nên chúng ta sẽ không cần tìm vùng không gian có hình ảnh trường hướng ra bên ngoài.
Kiến thức về trường có thể hoán đổi cho kiến thức về nguồn của nó (ít nhất là trong trường hợp trường tĩnh, không biến thiên). Nếu những sinh vật lạ nhìn thấy hình ảnh trường hấp dẫn của Trái Đất, họ có thể lập tức suy ra sự tồn tại của hành tinh, và ngược lại nếu họ biết khối lượng của Trái Đất, họ có thể tiên đoán ảnh hưởng của nó lên trường hấp dẫn xung quanh.
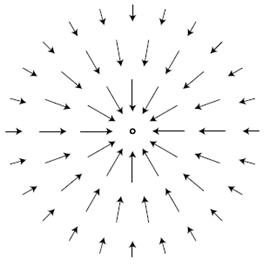
g/ Trường hấp dẫn xung quanh một cụm khối lượng giống như Trái Đất.
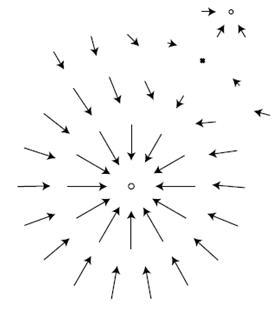
h/ Trường hấp dẫn của Trái Đất và Mặt Trăng chồng chất lên nhau. Lưu ý làm thế nào các trường triệt tiêu nhau tại một điểm, và làm thế nào không có ranh giới giữa các trường xuyên nhập vào nhau giữa hai vật thể.
Sự chồng chất trường
Một cơ sở rất quan trọng về mọi trường lực là khi có nhiều hơn một nguồn (hay bồn), các trường cộng lại với nhau theo quy luật cộng vectơ. Trường hấp dẫn nhất định sẽ có tính chất này, vì nó được định nghĩa dưới dạng lực tác dụng lên khối lượng thử, và lực cộng giống như cộng vectơ. Sự chồng chất là một đặc trưng quan trọng của sóng, nên tính chồng chất của các trường phù hợp với ý tưởng rằng sự nhiễu loạn có thể truyền ra bên ngoài dưới dạng sóng trong một trường.
Ví dụ 2. Sự giảm lực hấp dẫn tác dụng lên Io do sự hấp dẫn của Mộc tinh
Trường hấp dẫn trung bình trên vệ tinh Io của Mộc tinh là 1,81 N/kg. Trường hấp dẫn này giảm đi bao nhiêu khi Mộc tinh nằm ngay phía trước trên đầu ? Quỹ đạo của Io có bán kính 4,22 x 108 m, và khối lượng của Mộc tinh là 1,899 x 1027 kg.
Theo định luật lớp vỏ, chúng ta có thể xem Mộc tinh như thể toàn bộ khối lượng của nó tập trung tại tâm của nó, và tương tự đối với Io. Nếu chúng ta đến thăm Io và tiếp đất tại nơi mà Mộc tinh nằm ngay phía trên đầu, chúng ta cũng nằm trên đường thẳng nối liền hai tâm, nên toàn bộ bài toán có thể xem là một chiều, và phép cộng vectơ giống hệt như phép cộng vô hướng. Hãy sử dụng số dương cho trường hướng xuống (hướng vào tâm của Io) và số âm cho trường hướng lên. Thay số liệu thích hợp vào trong biểu thức thu được ở ví dụ 1, chúng ta tìm được đóng góp của Mộc tinh cho trường là – 0,71 N/kg. Sự chồng chất trường cho biết rằng chúng ta có thể tìm được trường hấp dẫn thật sự bằng cách cộng gộp các trường tạo ra bởi Io và Mộc tinh: 1,81 – 0,71 N/kg = 1,1 N/kg. Bạn có thể nghĩ sự suy giảm này sẽ tạo ra một số hiệu ứng kì lạ, và khiến cho Io là một đích đến du lịch lí thú. Thật ra thì bạn sẽ không phát hiện ra bất kì sự khác biệt nào nếu bạn bay từ phía bên này của Io sang phía bên kia. Đấy là do cơ thể bạn và Io đều chịu sức hấp dẫn của Mộc tinh, nên bạn cũng đi theo quỹ đạo cong trong không gian xung quanh Mộc tinh.
Sóng hấp dẫn
Một nguồn đứng yên sẽ tạo ra một hình ảnh trường tĩnh, giống như một quả cầu thép nằm yên bình trên tấm cao su. Một nguồn chuyển động sẽ tạo ra hình ảnh sóng trải rộng ra trong trường, giống như con côn trùng đang đạp nước trên mặt hồ. Mặc dù chúng ta đã khởi đầu với trường hấp dẫn là ví dụ đơn giản nhất của một trường tĩnh, nhưng các sao và hành tinh thật sự đang lướt đi hơn là chuyển động tại chỗ, nên sóng hấp dẫn không dễ gì phát hiện được. Lí thuyết hấp dẫn của Newton không mô tả sóng hấp dẫn, nhưng chúng được tiên đoán bởi thuyết tương đối rộng của Einstein. J.H. Taylor và R.A. Hulse đã được trao giải Nobel năm 1993 cho việc mang lại bằng chứng gián tiếp rằng sóng hấp dẫn của Einstein thật sự tồn tại. Họ đã phát hiện ra một cặp sao kì lạ, cực kì đậm đặc gọi là sao neutron đang quay xung quanh nhau rất gần, và chỉ ra rằng chúng đang mất dần năng lượng quỹ đạo ở tốc độ tiên đoán bởi lí thuyết của Einstein.

i/ Một phần của máy dò sóng hấp dẫn LIGO tại Dải đất hạt nhân Hanford, gần Richland, Washington. Nửa kia của máy dò nằm ở Louisiana.
Chương trình hợp tác Caltech-MIT đã xây dựng một cặp máy dò sóng hấp dẫn gọi là LIGO nhằm tìm kiếm bằng chứng trực tiếp hơn của sóng hấp dẫn. Vì về cơ bản chúng là những máy dò dao động nhạy nhất từng được chế tạo, nên chúng nằm ở những khu vực khá thôn dã, và các tín hiệu sẽ được so sánh giữa chúng để đảm bảo rằng chúng không phải do xe cộ chạy qua gây ra. Dự án bắt đầu hoạt động ở độ nhạy trọn vẹn vào năm 2005, và hiện nay có khả năng phát hiện một dao động gây ra sự thay đổi 10-18 m ở khoảng cách giữa các gương ở hai đầu ống chân không dài 4 km. Khoảng cách này lớn gấp một nghìn lần kích thước của hạt nhân nguyên tử! Chỉ có vừa vặn tiền tài trợ để giữ cỗ máy hoạt động trong vài ba năm nữa, nên các nhà vật lí chỉ có thể hi vọng trong thời gian đó, ở nơi nào đó trong vũ trụ, một biến động đủ dữ dội sẽ xảy ra để tạo ra một sóng hấp dẫn có thể phát hiện được. (Chính xác hơn là họ muốn sóng đó đến hệ Mặt Trời của chúng ta trong thời gian đó, mặc dù nó đã được tạo ra từ hàng triệu năm trước).
Trần Nghiêm dịch
Còn tiếp...