Con quỷ của Maxwell là một trong những thí nghiệm tưởng tượng nổi tiếng nhất trong vật lí học. Ở dạng thức truyền thống của nó, một con quỷ ngồi bên cạnh một khe hở nhỏ nối giữa hai phòng. Nó quan sát vận tốc của bất kì phân tử khí nào từ một phòng tiến về phía khe và chỉ mở khe khi vận tốc đó vượt quá một giá trị nhất định. Theo thời gian, con quỷ sẽ làm tăng nhiệt độ của một phòng đồng thời làm lạnh phòng kia – cái chúng ta biết là không thể nào về mặt nhiệt động lực học.
Theo thời gian, phạm vi bài toán con quỷ được mở rộng, vì các nhà nghiên cứu nhận ra vấn đề giống như vậy cũng áp dụng được cho nhiều bài toán đa dạng khác. Một phát biểu khác đến từ nhà vật lí Leo Szilard, ông lưu ý rằng bạn có thể có một động cơ-con quỷ. Hiện nay, sau 90 năm, các nhà nghiên cứu vừa triển khai thành công một động cơ Szilard hoạt động bởi một electron độc thân. Trong tiến trình, các nhà nghiên cứu xác nhận việc thiết lập bit kĩ thuật số của thông tin mô tả trạng thái của động cơ có một chi phí năng lượng.

Ở dạng thức ban đầu của nó, động cơ Szilard là một xilanh với hai piston ở hai đầu và một phân tử khí độc thân ở giữa. Trượt một vách ngăn ở giữa, thì phân tử khí sẽ chạy lên phần trên hoặc chạy xuống phần dưới. Như vậy sẽ đẩy một trong hai piston ra, mang lại khả năng thực hiện công “tự do” mà không cần cấp năng lượng. (Đây là một thí nghiệm tưởng tượng, hai piston được giả sử là chuyển động không có ma sát.) Sau đó bạn có thể loại bỏ vách ngăn, để cho xilanh cân bằng trở lại, và lặp lại toàn bộ quá trình bao nhiêu lâu tùy ý.
Động cơ Szilard còn giúp chứng minh năng lượng nhiệt động lực học và thông tin là tương đương nhau như thế nào. Khi động cơ đang hoạt động, mỗi công sinh ra là tương đương với một bit thông tin: nó cho bạn biết phân tử khí ở trong ngăn nào của xilanh. Dựa trên điều này, người ta có thể tính ra chi phí năng lượng của việc thiết lập hoặc xóa một bit. Trong vài năm trở lại đây, các nhà nghiên cứu đã bắt đầu triển khai các phiên bản đơn giản hóa con quỷ của Maxwell, cho phép họ kiểm tra những tính toán này có áp dụng đúng trong thế giới thực tế hay không.
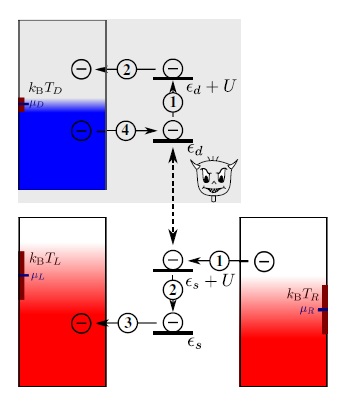
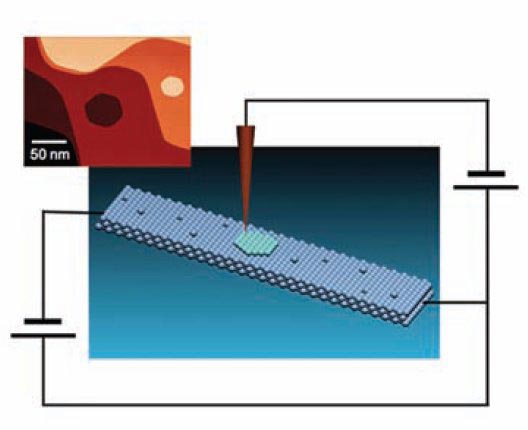
Cuối cùng thì một đội nghiên cứu quốc tế đã quyết định giải bài toán động cơ Szilard. Trong phiên bản triển khai của họ, phân tử chất khí được thay bằng điện tích của một electron độc thân. Điện tích đó được giữ ở một trong hai vị trí ngăn cách nhau bởi một hàng rào cho phép sự chui hầm lượng tử. Khi hệ được cho hoạt động tự do, thì điện tích bổ sung đó sẽ chui hầm ngẫu nhiên tới lui giữa hai vị trí.
Tới lượt con quỷ. Ở gần một trong hai vị trí, các nhà nghiên cứu đặt một bộ cảm biến có thể ghi nhận vị trí đó có mang điện tích hay không. Nếu nó ghi nhận, thì thiết bị sẽ thiết lập một điện áp lên hệ thống, nó sẽ vừa đủ để bắt giữ electron ở phía bên đó của hàng rào. Mặc dù việc này không thực hiện bất kì công có ích nào, nhưng nó tương đương với việc thiết lập giá trị của một bit, từ vô định (chẳng ai biết electron có thể ở đâu) đi tới xác định (electron ở một vị trí nhất định).
Kết quả đó không có gì hấp dẫn lắm, ngoại trừ thực tế là toàn bộ quá trình tiêu tốn một năng lượng rất nhỏ, cái được các tác giả cung cấp bởi một nguồn nhiệt. Khi con quỷ liên tục lặp lại việc bắt giữ và phóng thích electron, chi phí năng lượng tiếp tục cộng dồn lại. Có một sự giảm tương ứng nhiệt độ của bể nhiệt cấp năng lượng cho toàn hệ thống.
Độ giảm nhiệt độ này cho phép các tác giả đo lấy chi phí năng lượng của việc thiết lập một bit. Mặc dù hệ được làm lạnh gần không độ tuyệt đối, nhưng vẫn có một chút thăng giáng nhiệt ngẫu nhiên trong nó. Và với các phép đo vừa đủ, các tác giả có thể xác định giá trị của chi phí năng lượng xấp xỉ bằng giá trị được dự đoán bởi nghiên cứu lí thuyết. Các nguyên lí nhiệt động lực học vẫn giữ nguyên giá trị.
Nguồn: 10.1073/pnas.1406966111, arstechnica.com