- Matthew Rave và Marcus Sayers (Tạp chí The Physics Teacher, số tháng 11/2013)
Bài toán động học sau đây đã được ra làm đề bài dự án cho nhiều thế hệ học sinh học vật lí giải tích năm thứ nhất. Học sinh được yêu cầu giữ một quyển ghi ghép lại mọi công việc của họ và được khuyến khích giữ lại cả giấy nháp của họ. Mục tiêu của dự án là cho học sinh trải nghiệm quá trình làm vật lí lí thuyết, bằng cách tiến hành một dự án dễ trình bày khái niệm nhưng khó đến bất ngờ trong lúc giải. Giả sử Tarzan đang chạy về phía một dây leo treo thẳng đứng bên dưới một cái cây. Mục tiêu của anh ta là đu dây qua một khe núi. Hỏi Tarzan nên buông dây ra tại điểm nào để tăng tối đa khả năng bay sang bờ bên kia của vách đá (xem Hình 1)?
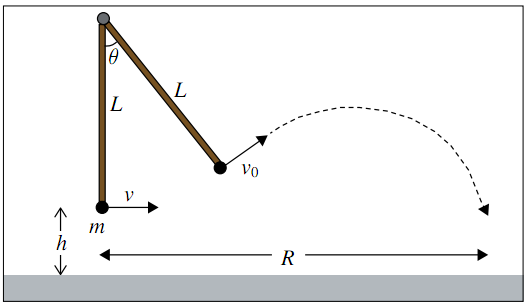
Hình 1. Nan đề Tarzan
Chúng tôi gọi đây là “nan đề” bởi vì có hai yếu tố đang cạnh tranh nhau. Một mặt, Tarzan buông dây càng sớm thì anh ta sẽ có vận tốc càng lớn. Mặt khác, anh ta giữ dây càng lâu thì anh ta sẽ đu thêm quãng đường nhiều hơn phía trên khe núi và góc nhảy ban đầu sau khi anh ta buông ra sẽ càng lớn. Câu hỏi đặt ra là, góc buông ra bằng bao nhiêu thì tăng tối đa tầm xa của anh ta?
Trực giác vật lí ở đây bị hạn chế, trừ khi người ta có thể đi ra ngoài hồ bơi và đu dây cao su để thử. Dự đoán đầu tiên của các tân học sinh là góc buông ra bằng 45o, vì đó là góc tối ưu để ném xiên trên một mặt ngang. Nhưng đây chỉ là dự đoán.
Để tiếp tục, ta cần một vài giả thiết. Giả sử sợi dây leo không khối lượng vẫn căng trong suốt thời gian; sợi dây chiều dài L và điểm dưới của nó ban đầu có độ h so với đất. Giả sử Tarzan là một chất điểm khối lượng m và anh ta chộp sợi dây ngay tại điểm dưới của nó. (Giả thiết này tương ứng với giả định rằng khối tâm của Tarzan ở ngang mức với điểm dưới của sợi dây, cho dù thật ra anh ta nắm sợi dây ở chỗ nào.) Giả sử một vận tốc ban đầu v theo phương ngang. Chúng ta muốn tăng tối đa quãng đường đi theo phương ngang cho đến điểm chạm đất, khi đo từ vị trí ban đầu của khối lượng trên sợi dây leo, chứ không phải từ điểm buông ra. Thành ra bề rộng của khe núi là không có liên quan, trừ khi chúng ta muốn biết liệu Tarzan có rơi xuống khe núi hay không. Lực ma sát và sức cản không khí sẽ được bỏ qua.
Lưu ý rằng những giả thiết này không phải là tầm thường đối với học sinh. (Một học sinh từng đề xuất rằng tầm xa phụ thuộc vào bề rộng của khe núi.) Cho đến khi học sinh có được kinh nghiệm lí thuyết, có lẽ cần có nhiều chỉ dẫn và gợi ý. Khi nhận dạng bài toán này thuộc loại nào, học sinh của chúng ta lập tức nhận ra tầm quan trọng của những phương trình động học cơ bản. Có học sinh nói “Ồ! Đây là một bài tập ‘Chương 4’.” Sau khi đối chiếu và phân tích kĩ hơn, học sinh sẽ nhận thấy sự bảo toàn năng lượng tỏ ra có ích như thế nào trong phân tích chuyển động đu đưa của sợi dây leo.
Cái hữu ích đối với học sinh là trước tiên xét những bài toán đơn giản, sau đó mới tăng dần tính phức tạp. Trước tiên, ta nhắc lại công thức tính tầm xa của vật bị ném trên một mặt phẳng. Đối với một vật bị ném với vũ trụ ban đầu v0 hợp một góc θ so với phương ngang, đa số sách vở suy luận ra kết quả

trong đó R là tầm xa, và chúng ta lấy g = + 9,8m/s2. (Xem Chương 4, sách của Serway1.) Để học sinh tiến hành suy luận ra công thức trên là không cần thiết lắm; kết quả [phương trình (1)] sẽ được dùng làm viên gạch cơ sở cho lời giải cuối cùng cho toàn bộ bài toán Tarzan.
Tiếp theo, xét tầm xa của vật ném (một lần nữa với vận tốc ban đầu v0 và góc ban đầu θ) được ném từ rìa của một vách đá có độ cao H so với đất. Đây là một bài toán động học hai chiều; áp dụng biểu thức
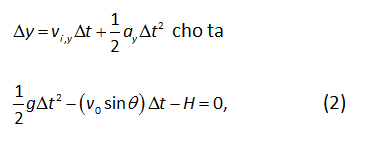

Kết quả trung gian này [phương trình (4)] biểu hiện một số phương diện vật lí thú vị (và bất ngờ), và ở đây ta nên dừng lại một chút để học sinh phản hồi về cái họ vừa tìm thấy. Chẳng hạn, học sinh của chúng ta bất ngờ khi thấy rằng “góc tối ưu” cho tầm xa cực đại (được tìm bằng cách đặt dR/dθ = 0) giảm khi độ cao H tăng. (Đối với những vách đá cực cao, người ta nên ném vật theo phương ngang để có tầm xa tối đa.) Ở đây, các phần mềm đại số (như Maple hay Mathematica) có thể có giá trị lớn đối với học sinh trong việc hình dung sự phức tạp của phương trình (4) và trong khảo sát các giới hạn. Tuy nhiên, phần mềm là không cần thiết; học sinh của chúng ta có thể thu được đồ thị mà chỉ dùng Excel thôi.
A. Nan đề Tarzan: Bài giải
Bây giờ là lúc chúng ta giải trực tiếp nan đề Tarzan. Vì chúng ta chưa biết vận tốc v0 mà Tarzan rời khỏi dây leo, nên chúng ta bắt đầu bằng việc áp dụng định luật bảo toàn cơ năng cho hệ ở hai cấu hình như ở Hình 2: (1) là nơi dây leo treo thẳng đứng (lúc Tarzan ban đầu nắm lấy dây), và (2) là nơi dây leo nghiêng một góc θ (khi Tarzan buông dây).
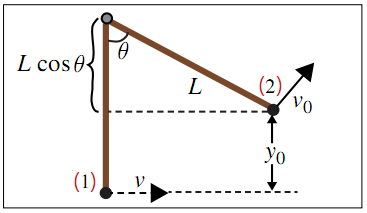
Hình 2. Sử dụng định luật bảo toàn năng lượng. Cấu hình ban đầu là (1); cấu hình cuối cùng là (2), khi Tarzan buông sợi dây ra.
Chọn thế năng của hệ bằng không cho cấu hình (1) (sao cho E1 thuần túy là động năng), ta thấy rằng E1= E2 mang lại
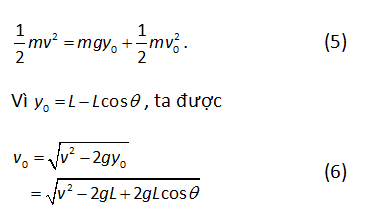
Lưu ý rằng chúng ta giả sử vận tốc ban đầu của Tarzan đủ để đạt tới bất kì góc nào từ 0 tới 90o.
Tầm xa tính từ điểm Tarzan buông dây (gọi giá trị này là R2) có thể tính được bằng cách thay phương trình (6) vào phương trình (4). Nghiệm cho bài toán – nghĩa là tầm xa R1 đo từ vị trí của Tarzan trong cấu hình (1) – khi đó đơn giản bằng Lsinθ + R2. Do đó, kết quả cuối cùng là
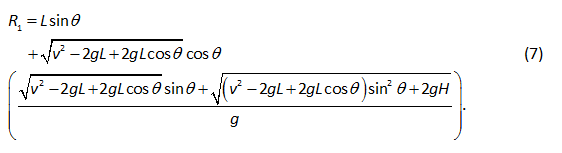
trong đó chúng ta lưu ý rằng H = h + y0 = h + L – L cosθ. Tầm xa này là một hàm của góc buông dây θ sẽ được học sinh vẽ biểu diễn trên đồ thị như ở Hình 3, với những giá trị hợp lí cho v, h và L. Từ đồ thị ta dễ dàng ước tính được góc cho tầm xa cực đại. Tất nhiên, để có độ chuẩn xác cao hơn, người ta có thể đặt dR1/dθ = 0 và giải cho θ, mặc dù trong trường hợp này có lẽ cần đến sự trợ giúp tính toán bằng số.
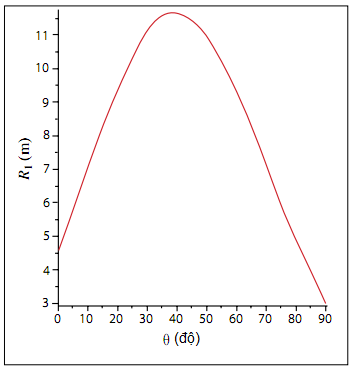
Hình 3. Tầm xa tính từ điểm tiếp xúc với dây leo ban đầu là một hàm của góc buông dây. (v = 10 m/s, h = 1 m, L = 3 m). Với những giá trị này, tầm xa cực đại ứng với góc θ = 39,4o.
Học sinh của chúng ta nên tìm ra vài trường hợp giới hạn thật hấp dẫn. Khi Tarzan chạy rất nhanh (lấy giới hạn v tiến tới vô cùng) thì biểu thức cho thấy góc lí tưởng (để tăng tối đa R1) là 45o, giống như trường hợp một vật bị ném trên mặt ngang. Đây là bởi vì tốc độ của Tarzan không thay đổi bao nhiêu trong lúc đu dây nếu v rất lớn, nên việc đu trên sợi dây chỉ giữ một vai trò nhỏ trong xác định tầm xa. Tuy nhiên, khi v nhỏ, học sinh để ý thấy một điều kì lạ xảy ra: những “khe trống” xuất hiện trên đồ thị của R1 là một hàm của θ. Sau nhiều chỉ dẫn, cuối cùng học sinh nhận ra rằng cần có một lượng động năng tối thiểu để cho Tarzan đạt tới một độ cao nhất định, nên vận tốc ban đầu v đặt một ràng buộc lên góc buông θ để có ý nghĩa vật lí. Các “khe trống” trên đồ thị tương ứng với những giá trị của v mà đối số trong căn bậc hai bị âm.
Tốc độ tối thiểu để đạt tới một góc θ nhất định được cho bởi

Công thức dễ dàng có được bằng cách sử dụng định luật bảo toàn năng lượng một lần nữa. Với giá trị mẫu L = 3 m, tốc độ tối thiểu để đạt tới một góc bất kì lên tới 90o là 7,67 m/s. Khi học sinh sử dụng giá trị của v thấp hơn ngưỡng này, thì đồ thị của họ hết ý nghĩa vật lí trên một góc tới hạn nhất định được cho bởi θc = cos-1 [1 – v2/(2gL)]. (Với những tốc độ lớn hơn vmin, không có nghiệm cho phương trình θc này, cho nên không có ngưỡng trên – nghĩa là mọi góc đều là có thể.)
Tác dụng làm biến thiên chiều dài dây leo L cũng thú vị. Với L nhỏ, phương trình (7) trở thành phương trình (4), cho thấy sợi dây không có vai trò gì trong việc xác định tầm xa (đúng như người ta trông đợi). Với L lớn, một lần nữa lại có một góc ngưỡng, ở trên giá trị đó sẽ không có nghiệm nào vì một trong các căn số lại có đối số âm. Trong trường hợp tốc độ của Tarzan không đủ để đạt tới một góc như thế, vì động năng ban đầu của anh ta giới hạn thế năng trọng trường nên anh ta có thể buông dây muộn.
Cuối cùng, cũng nên lưu ý rằng góc buông dây tối ưu giảm khi độ cao h tăng, vì khi h tiến tới vô cùng thì góc buông tiến tới bằng không. Điều này phản ánh những giới hạn của phương trình (4). Một học sinh nói như thế này: “Bạn càng cao thì nên buông dây ra càng sớm.”
Với những học sinh yêu thích vật lí, bài toán này còn có nhiều chỗ để khai thác. Nghiên cứu mới đây2 cho biết ít nhất có thêm ba chỗ nữa để tiếp tục khai thác.
B. Bài học rút ra
Những học sinh tham gia hoạt động này nghĩ rằng nó mang tính giới thiệu cách giải quyết vấn đề. Một học sinh nói “[nó mở rộng] cửa cho những bài toán phức tạp hơn nhiều có thể được giải theo kiểu giống hệt như vậy”. Ý tưởng là bài toán phức tạp có thể được chia thành các phần đơn giản hơn để dễ bắt tay vào giải hơn. Loại phương pháp “chia để trị” này nên được áp dụng thường xuyên hơn trong các khóa học vật lí căn bản.
Học sinh còn đánh giá đúng sức mạnh của vật lí lí thuyết so với thực nghiệm. Nghĩa là, họ bất ngờ khi thấy những kết quả lí thuyết có thể mang tính tổng quát như thế nào. Một thí nghiệm kiểu-Tarzan trên thực tế3 có thể mang lại kết quả, nhưng những kết quả này sẽ bị hạn chế bởi chiều dài của dây leo, tốc độ của người tham gia, và vân vân. Một tính toán trên lí thuyết sẽ mang lại một kết quả hoàn toàn khái quát, cho mọi L, v và h.
Những học sinh khác thì nói ưu điểm của hoạt động này nằm ở chỗ nó là một bài thực hành lớn với kĩ năng toán học và kĩ năng dùng máy tính; nó là “tiếng gọi thức tỉnh” về cái vật lí học đòi hỏi; nó cho thấy phương pháp “thử-sai” có thể hữu ích như thế nào trong khoa học; và việc giải xong mang lại cho học sinh cảm giác thành tựu cá nhân. Một học sinh nói rằng “đã có những lúc hoang mang và thất vọng”, nhưng cuối cùng bài toán bổ sung rất nhiều kiến thức để hiểu rõ các phương pháp lí thuyết.
Chúng tôi khép lại vấn đề với một trích dẫn từ Lewis4: “[Chúng ta] không nên xem việc đạt tới các sự thật là mục tiêu chủ yếu của việc giảng dạy. Các khái niệm, là những khuôn mẫu trí tuệ được xây dựng trên các sự thật, có thể tồn tại lâu hơn.” Hi vọng của chúng tôi là những học sinh tiếp tục nỗ lực tìm hiểu một bài toán lí thuyết (ví dụ như nan đề Tarzan) sẽ tiến gần hơn đến chỗ suy nghĩ giống như một nhà vật lí.
Tài liệu tham khảo
1. R. Serway và J. Jewett, Physics for Scientists and Engineers, 8th (Brooks/Cole, 2010).
2. H. Shima, “How far can Tarzan jump?” arXiv:1208.4355v1 (2012).
3. K. P. Trout và C. A. Gaston, “Active-learning physics experiments using the Tarzan swing,” Phys. Teach. 39, 160–163 (3/2000).
4. Teaching School Physics, J. Lewis biên tập (Penguin Books, 1972), trang 74.
Trần Nghiêm dịch ◊