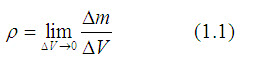- Michael de Podesta (Physics World, tháng 8/2013)
Đo chính xác nhiệt độ là một khâu trọng yếu trong hầu hết mọi thí nghiệm khoa học, và trong đa số trường hợp, phép đo nhiệt độ là tương đối đơn giản. Tuy nhiên, cùng với các đồng nghiệp của tôi, Robin Underwood và Gavin Sutton tại Phòng thí nghiệm Vật lí Quốc gia (NPL) ở Anh, tôi đã dành ra sáu năm đo một nhiệt độ - và chúng tôi biết đáp án trước khi bắt đầu!
Mỗi phép đo là so sánh một lượng đã biết của một đại lượng với một lượng chuẩn của đại lượng đó. Nhưng trong đa số phép đo, việc so sánh dựa theo chuẩn này là gián tiếp và không hiển hiện ngay trước mắt người dùng. Ví dụ, khi bà chủ cửa hàng tạp hóa cân 500 g nho, cả người bán lẫn người mua đều không nhận thức ngay được dây chuyền chế tạo kết nối từ cửa hàng, qua phòng thí nghiệm “cân nặng và đo lường” ở địa phương, đến NPL và đến một khối kim loại độc nhất vô nhị đặt trong tầng hầm của Cục Cân nặng và Đo lường Quốc tế (BIPM) ở Paris, đó là chuẩn kilogram của chúng ta.
Với nhiệt độ, lượng chuẩn để mọi nhiệt độ khác được so sánh là nhiệt độ của điểm ba của nước, TTPW. Đa số mọi người sử dụng cặp nhiệt điện để đo nhiệt độ của lò vi sóng không nhận thức được điều này. Nếu bạn có đến NPL, bạn sẽ thấy một bình chân không có các ngăn thủy tinh chứa nước ở điểm ba của nó, đó là nhiệt độ chúng tôi dùng để xác định trực tiếp các số đo trên nhiệt kế.
Tại nhiệt độ điểm ba, nước lỏng, nước đá và hơi nước đồng thời tồn tại trong trạng thái cân bằng và nhiệt độ này được chọn làm nhiệt độ chuẩn vì nó có thể được tái tạo tương đối dễ dàng với sai số dưới 0,001oC. Hiện nay, TTPW được định nghĩa chính xác là 273,16 K (hay 0,01oC). Các nhà khoa học có thể chọn bất kì con số nào cho nhiệt độ này, nhưng sự lựa chọn đặc biệt này là để cho độ lớn của một kelvin và một độ Celsius bằng sát với độ bách phân trong lịch sử.
Định nghĩa này đã phục vụ tốt cho chúng ta trong hơn 50 năm qua. Nhưng đối với nhiều nhà khoa học – trong đó có bản thân tôi – nó là chưa thỏa đáng. Lí do nhiệt độ được định nghĩa theo cách này là vì dấu ấn của thực tế là chúng ta đã biết đo nhiệt độ trước khi chúng ta hiểu nhiệt độ là cái gì. Nếu hồi 200 năm trước, chúng ta đã hiểu nhiệt độ là một số đo của năng lượng của chuyển động nguyên tử, thì chúng ta đã định nghĩa nhiệt độ trực tiếp theo năng lượng. Và đó là cái chúng tôi hiện đang hi vọng sẽ làm được.
Trong cơ học thống kê, nhiệt độ luôn luôn xuất hiện cùng với hằng số Boltzmann, kB. Hiện nay, vì TTPW được định nghĩa chính xác, nên nếu người ta đo tích kBTTPW thì toàn bộ sai số ở tích đó được biểu diễn là sai số ở kB. Chúng tôi nghĩ đây là cái không hợp lí và kB – như tên gọi của nó cho thấy – nên là một hằng số, và nên được định nghĩa chính xác.
Với quan niệm này thì kelvin sẽ được định nghĩa theo kB – giống như tốc độ ánh sáng trong chân không – nó sẽ có một giá trị chính xác mà không có sai số đo nào nữa. Vì đơn vị của kB là joule/kelvin, nên cách này sẽ liên hệ nhiệt độ trực tiếp với năng lượng, và gắn kết nó chặt chẽ với phần còn lại của Hệ Đơn vị Quốc tế (SI). Khi đó, trong tương lai, mỗi phép đo nhiệt độ về cơ bản sẽ là một phép đo năng lượng của các nguyên tử và phân tử.
Nghiên cứu của chúng tôi là một bộ phận của một nỗ lực sâu rộng hơn nhằm định nghĩa lại các đơn vị cơ bản của SI theo các hằng số tự nhiên. Giây và mét đã được định nghĩa theo cách này, và các nhà đo lường học trên khắp thế giới đang bận tìm cách đạt tới mục tiêu tương tự cho kilogram, ampere và mole.

Một bán cầu đã được xử lí hoàn hảo – một nửa của một bộ cộng hưởng gần-cầu dùng để đo hằng số Boltzmann. Ảnh: Michael de Podesta/NPL
Phương pháp sử dụng âm thanh
Phương pháp đo kBTTPW của chúng tôi lấy tiêu chí là làm cho cuộc sống của chúng ta thuận tiện hơn và chọn hệ một hệ vật lí trong đó chúng ta có thể đạt được sai số khả dĩ thấp nhất. Hồi năm 2007, chúng tôi đã suy nghĩ rất nhiều về mọi khả năng và đã chọn thực hiện một phép đo tốc độ của âm thanh trong một chất khí đơn nguyên tử. Có hai lí do thuyết phục cho sự lựa chọn này.
Thứ nhất, tốc độ của âm thanh trong giới hạn của áp suất thấp, c0, trong một chất khí đơn nguyên tử tỉ lệ thuận với căn bậc hai của tốc độ của các phân tử, vRMS, theo liên hệ đơn giản đến bất ngờ c0 = √(5/9)vRMS. Cho nên, nếu chúng ta có thể đo c0 với sai số thấp, thì, nếu chúng ta đã biết khối lượng của các phân tử, m, chúng ta có thể ước tính trực tiếp động năng trung bình của các phân tử, ½mv2RMS. Cơ học thống kê cho chúng ta biết rằng đối với một chất khí phân tử mật độ thấp thì động năng này bằng 3 × ½kBT. (Xem phần phụ chú ở cuối bài để rõ hơn về các phương trình này.)
Lí do thứ hai khiến chúng tôi chọn đo tốc độ của âm thanh trong một chất khí đơn nguyên tử là vì ta có thể thực hiện các phép đo chính xác đến bất ngờ của giá trị này. Phương pháp hiển hiện nhất để làm việc này là đo thời gian cần thiết cho một sóng âm truyền đi một khoảng cách cố định. Phép đo càng chính xác khi khoảng cách liên quan càng dài nhưng bù lại việc biết nhiệt độ trên toàn lộ trình sẽ rất khó. “Thủ thuật” là sử dụng một bộ cộng hưởng.
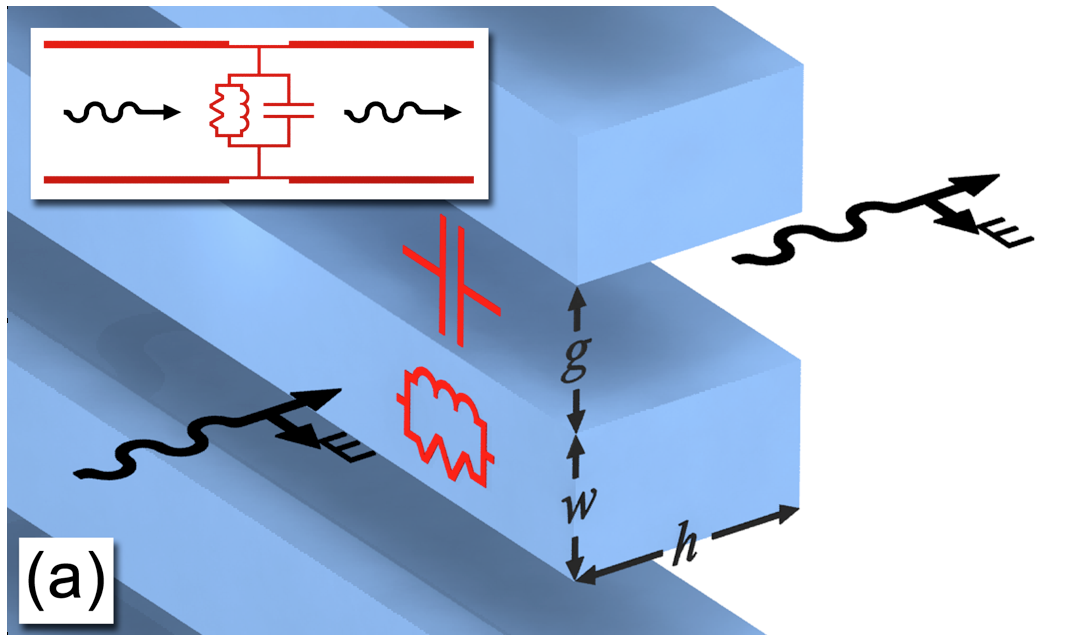
Trong kĩ thuật này, người ta “gấp ngược” đường truyền âm thanh để chúng phản xạ tới lui bên trong một hộp cộng hưởng. Thông thường, sóng sau mỗi lần phản xạ giao thoa triệt tiêu với sóng đến từ loa và mức áp suất sóng bên trong bộ cộng hưởng là thấp. Tuy nhiên, nếu người ta chọn một tần số mà bội lần bước sóng khớp chính xác với kích cỡ của bộ cộng hưởng, thì sự giao thoa tăng cường – hay cộng hưởng – xảy ra. Bằng cách đo tần số xảy ra cộng hưởng, người ta có thể suy luận ra tốc độ của âm thanh, với kích cỡ của bộ cộng hưởng là đã biết.
Một trong những ưu điểm chính của kĩ thuật này là tốc độ của âm thanh có thể được tìm độc lập với một vài cộng hưởng khác nhau biến thiên tần số từ khoảng 2 đến 20 kHz. Vì thế, mức ăn khớp của chúng cung cấp một chi tiết tự kiểm tra. Vấn đề là mặc dù tần số có thể được đo rất chính xác, nhưng cái khó hơn nhiều là đo kích cỡ của bộ cộng hưởng. Và cái còn khó hơn nữa là kích cỡ đó tất nhiên sẽ biến thiên theo nhiệt độ và áp suất. Do đó, chúng ta phải chọn rất kĩ hình dạng của bộ cộng hưởng.
Trong nghiên cứu của chúng tôi tại NPL, chúng tôi sử dụng một bộ cộng hưởng hình ellipoid ba trục. Nó có dạng cầu gần như hoàn hảo, ngoại trừ là các bán kính x, y và z của nó, mỗi bán kính xấp xỉ 6 mm, sai lệch nhau khoảng ±0,05% (32 µm). Cái nghe có vẻ lạ là việc làm biến dạng một hình cầu hóa ra mang lại một phép đo tốt hơn, nhưng thật sự đúng là như thế. Nguyên nhân là vì chúng tôi sử dụng các cộng hưởng vi sóng để đo kích cỡ bên trong của bộ cộng hưởng và – không giống như cộng hưởng âm – cộng hưởng vi sóng bị tiêu tán bên trong một hình cầu. Điều này không có nghĩa là các cộng hưởng thiếu chất lượng; thay vậy nó có nghĩa là có một vài cộng hưởng cùng một tần số. Biến dạng ba trục mà chúng tôi tạo ra làm “nâng” sự suy sụp này lên, cho phép chúng tôi đo một tần số cộng hưởng cho mỗi bán trục chính. Khả năng của chúng tôi đo đồng thời bán kính x, y và z với độ chính xác nano mét và đo cộng hưởng âm có nghĩa là mọi sự giãn nở nhiệt bất kì của bộ cộng hưởng đều có thể được xét đến.
Cuối cùng, chúng tôi làm lạnh thí nghiệm xuống đến TTPW. Chúng tôi biết nhiệt độ đó chính xác bởi vì trước đó chúng tôi đã chế tạo sáu nhiệt kế trong một bình chứa nước, nước đá và hơi nước trong chân không. Chúng tôi mang những nhiệt kế này vào thiết bị của chúng tôi mà không ngắt kết nối với dây dẫn, vì sự biến thiên điện áp có thể gây biến thiên nhiệt độ.
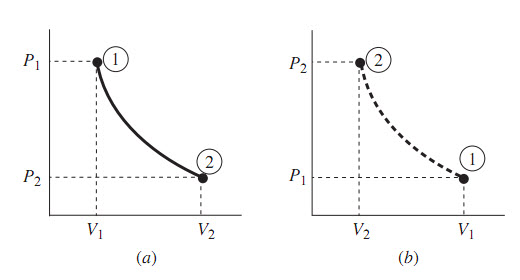
Thí nghiệm của chúng tôi hoạt động như sau. Bằng cách đo các tần số cộng hưởng vi sóng, chúng tôi có thể ước tính kích cỡ và hình dạng của bộ cộng hưởng. Sau đó, biết kích cỡ và hình dạng của bộ cộng hưởng rồi thì các phép đo tần số cộng hưởng âm cho phép chúng tôi suy luận ra tốc độ của âm thanh. Chúng tôi đã đo tốc độ âm thanh của bảy cộng hưởng ở những áp suất khác nhau và ngoại suy đến giới hạn áp suất zero (Hình 1). Từ đây chúng tôi biết được tốc độ giới hạn áp suất thấp của âm thanh, c0, và rồi chúng tôi có thể suy luận ra tốc độ phân tử trung bình và do đó động năng phân tử trung bình, và từ đó suy ra kBT. Và cuối cùng, vì chúng tôi đã tiến hành thí nghiệm tại nhiệt độ TTPW, nhiệt độ hiện nay được định nghĩa chính xác, nên chúng tôi có thể suy luận ra kB với sai số thấp.
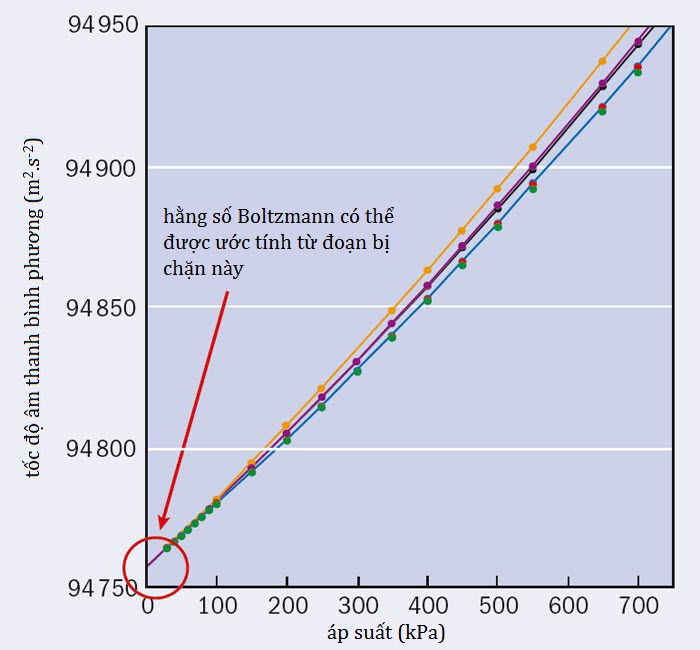
Hình 1. Phép tính trọng yếu trong thí nghiệm của chúng tôi là phép tính tốc độ của âm thanh tại giới hạn của áp suất thấp, c0, của khí argon trong bộ cộng hưởng của chúng tôi ở nhiệt độ điểm ba của nước. Không thể đạt tới áp suất bằng không, tức là chân không hoàn hảo, nhưng ngoại suy một vài số đo của tốc độ âm thanh (bình phương) trên một ngưỡng áp suất mang đến cho chúng tôi đáp số.
Loại thí nghiệm này – mà kết quả của chúng có thể ảnh hưởng đến giá trị được gán trong tương lai của hằng số Boltzmann – đòi hỏi tiếp cận rất dè dặt. Vì thế, chúng tôi không khẳng định có đáp số đúng. Cái chúng tôi đang khẳng định là chúng tôi có thể chứng minh đáp số đúng – cho dù nó là cái gì – không thể khác với đáp số của chúng tôi nhiều hơn sai số riêng của chúng tôi. Để làm công việc khẳng định so sánh này, chúng tôi cần tách kết quả cuối cùng thành một số kết quả con và đánh giá từng kết quả con theo những cách khác nhau và để ý xem đáp số thay đổi như thế nào. Trong thí nghiệm này, có ba phần khá riêng biệt: một phép đo cho biết chúng tôi đạt gần tới TTPW bao nhiêu; một phép đo khối lượng phân tử của khí argon mà chúng tôi sử dụng; và một phép đo tốc độ của âm thanh, cái lệ thuộc nhiều vào kích cỡ và hình dạng của bộ cộng hưởng.
Thật đáng tiếc là biên tập viên Physics World từ chối đăng toàn văn phần kĩ thuật tính toán này, cho nên dưới đây chúng tôi tập trung nói vào hai chi tiết chính của phép đo: ước tính bán kính của bộ cộng hưởng và ước tính tốc độ của âm thanh.
Trần Nghiêm dịch
>> Còn tiếp Phần 2