Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§23. Trường tĩnh điện được mô tả như thế nào?
GV: Ta sẽ tiếp tục nội dung thảo luận đã nêu ở bài trước với câu hỏi: Một trường tĩnh điện được mô tả như thế nào?
HS B: Một trường tĩnh điện được mô tả bởi một đặc trưng lực vector gọi là cường độ điện trường. Tại mỗi điểm trong điện trường, cường độ E có một hướng và một giá trị số xác định. Nếu chúng ta dịch chuyển từ một điểm này trong điện trường sang một điểm khác theo kiểu sao cho chiều của các vector cường độ điện trường luôn luôn tiếp tuyến với hướng dịch chuyển, thì quỹ đạo của những dịch chuyển như thế được gọi là đường sức điện trường. Các đường sức rất tiện lợi để mô tả một trường trên phương diện hình học.
GV: Tốt. Bây giờ chúng ta hãy giải thích chặt chẽ hơn. Lực tương tác Coulomb giữa hai điện tích q1 và q2 cách nhau một khoảng r có thể được viết ở dạng

Phương trình (128) nghĩa là điện tích q1 tạo ra điện trường xung quanh nó, có cường độ tại điểm cách nó khoảng cách r là q1/r2. Phương trình (129) nghĩa là trường này tác dụng lên điện tích q2, nằm cách q1 một khoảng cách r, với một lực E(r)q2. Phương trình (127) có thể viết lại là nhờ nêu ra một đại lượng trung gian E, đặc trưng của trường. Các em hãy thử xác định phạm vi áp dụng của phương trình (127), (128) và (129).
HS B: Phương trình (127) có thể áp dụng cho hai điện tích điểm. Nghĩa là phạm vi áp dụng của phương trình (128) và (129) cũng giống như vậy. Ta thu được chúng từ phương trình (127).
GV: Điều đó chỉ đúng với phương trình (127) và (128). Phương trình (129) có phạm vi áp dụng rộng hơn nhiều. Cho dù cái gì tạo ra điện trường E (một điện tích điểm, một tập hợp gồm những điện tích điểm hay những vật tích điện có hình dạng tùy ý), trong mọi trường hợp lực tác dụng bởi trường này lên điện tích q0 bằng tích của điện tích này với cường độ điện trường tại điểm đặt điện tích q0. Dạng khái quát hơn của phương trình (129) là dạng vector như sau

Trong đó các mũi tên, như thường lệ, kí hiệu cho các vector. Rõ ràng từ phương trình (130) là chiều của lực tác dụng lên điện tích q0 tại điểm cho trước trong trường trùng với chiều của cường độ điện trường tại điểm này nếu điện tích q0 là dương. Nếu điện tích q0 là âm, thì chiều của lực ngược với chiều của cường độ điện trường.
Ở đây chúng ta có thể thấy sự độc lập của khái niệm trường. Những vật tích điện khác nhau tạo ra những trường tĩnh điện khác nhau, nhưng mỗi một trường này tác dụng lên một điện tích đặt trong nó theo quy luật giống nhau (130). Để tính lực tác dụng lên một điện tích, trước tiên các em phải tính cường độ điện trường tại nơi đặt điện tích đó. Vì thế, cái quan trọng là có thể tính được cường độ điện trường gây ra bởi một hệ điện tích. Giả sử có hai điện tích, q1 và q2. Độ lớn và chiều của cường độ điện trường gây ra bởi từng điện tích có thể tính được dễ dàng cho bất kì điểm nào trong không gian mà chúng ta đang xét. Giả sử tại một điểm nhất định,

Tôi nhắc lại lần nữa là các cường độ điện trường phải được cộng theo kiểu vector. (Quay sang HS A) Em có hiểu không nào?
HS A: Vâng, em biết là cường độ điện trường phải được cộng vector.
GV: Tốt. Bây giờ chúng ta có thể kiểm tra xem các em có thể vận dụng kiến thức này như thế nào trong thực tế. Hãy vẽ các đường sức điện trường của hai điện tích kích cỡ bằng nhau và trái dấu (+q1 và – q2), giả sử rằng một trong hai điện tích (chẳng hạn, +q1) có độ lớn gấp điện tích kia vài lần.
HS A: Em e là em không thể vẽ. Chúng ta chưa từng nói tới những trường như thế trước đây.
GV: Vậy em đã học những loại trường nào rồi?
HS A: Em biết hình ảnh các đường sức điện trường trông như thế nào cho một điện trường gây ra bởi hai điện tích điểm bằng nhau về độ lớn. Em vẽ được một hình như thế ở Hình 86.
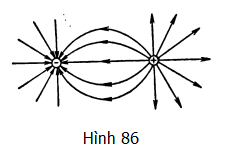
GV: Hình vẽ của em có phần không chính xác, mặc dù về mặt định tính nó thật sự miêu tả các đường sức điện trường gây ra bởi hai điện tích điểm bằng nhau về độ lớn và trái dấu. Sao em không hình dung xem bức tranh này sẽ thay đổi như thế nào nếu một trong hai điện tích tăng lên?
HS A: Chúng em chưa từng làm cái gì giống như vậy.

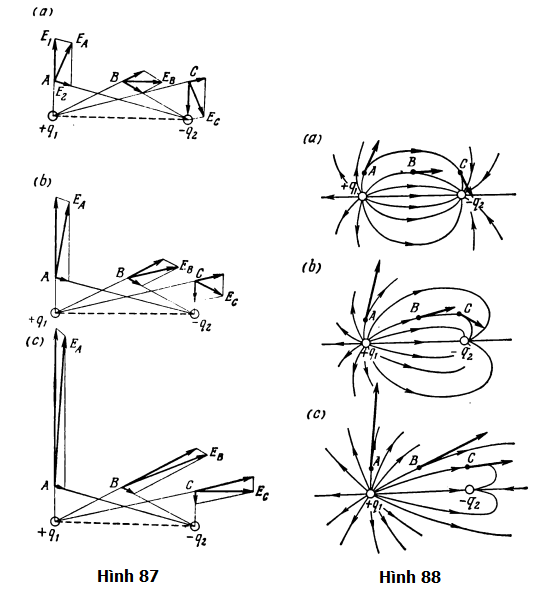
Như các em thấy, tác dụng của điện tích +q1 tăng lên theo sự tăng độ lớn tương đối của nó; điện trường của điện tích +q1 bắt đầu lấn át điện trường của điện tích – q2.
HS A: Giờ thì em đã hiểu cách dựng hình ảnh đường sức của điện trường gây ra bởi một hệ gồm vài ba điện tích.
GV: Chúng ta hãy tiếp tục thảo luận về trường tĩnh điện. Trường này có một tính chất quan trọng đặt nó vào quan hệ tương tự với trường hấp dẫn, đó là: công thực hiện bởi lực của trường tính theo những quỹ đạo khép kín là bằng không. Nói cách khác, nếu điện tích chuyển động trong điện trường quay trở lại vị trí xuất phát ban đầu của nó, thì công thực hiện bởi lực điện trường trong chuyển động này là bằng không. Trên vài đoạn nhất định của quỹ đạo công này sẽ có giá trị dương và trên những đoạn khác là âm, nhưng tổng công thực hiện sẽ bằng không. Có những hệ quả thú vị từ tính chất này của trường tĩnh điện. Các em có thể gọi tên chúng không?
HS B: Không, em không nghĩ ra hệ quả nào.
GV: Tôi sẽ giúp em. Có lẽ em đã để ý rằng các đường sức của một điện trường không bao giờ cắt qua nhau. Chúng bắt đầu và kết thúc ở các điện tích (đi ra ở điện tích dương và đi vào ở điện tích âm) hoặc chúng kết thúc ở vô cùng (hoặc chúng xuất phát từ vô cùng). Em có thể liên hệ trường hợp này với tính chất vừa nói của trường tĩnh điện hay không?
HS B: Giờ thì em hiểu rồi. Nếu một đường sức trong một trường tĩnh điện tự khép kín, thì bằng cách lần theo nó chúng ta có thể trở lại điểm ban đầu. Khi một điện tích chuyển động theo một đường sức, dấu của công thực hiện bởi điện trường rõ ràng không thay đổi và, do đó, không thể nào bằng không. Mặt khác, công thực hiện theo một quỹ đạo khép kín bất kì phải bằng không. Do đó, các đường sức của một trường tĩnh điện không thể nào khép kín.

GV: Khá chính xác. Còn có một hệ quả nữa từ tính chất vừa nói của trường tĩnh điện: công thực hiện khi dịch chuyển một điện tích từ điểm này sang điểm khác trong trường không phụ thuộc vào hình dạng đường đi. Chúng ta có thể di chuyển một điện tích từ điểm a sang điểm b, chẳng hạn, theo những quỹ đạo khác nhau, 1 và 2 (Hình 89). Ta hãy kí hiệu A1 là công thực hiện bởi lực điện trường làm dịch chuyển điện tích theo đường đi 1 và công đó theo đường đi 2 là A2. Ta xét một vòng kín: từ điểm a đến điểm b theo đường đi 1 và từ điểm b trở lại điểm a theo đường đi 2. Khi trở lại theo đường đi 2, công thực hiện sẽ là – A2. Công toàn phần thực hiện trong một vòng kín là A1 + (- A2) = A1 – A2. Vì công thực hiện theo đường đi khép kín bất kì nào là bằng không, nên A1 = A2. Thực tế công thực hiện làm dịch chuyển một điện tích độc lập với đường đi đã chọn mà chỉ phụ thuộc vào điểm đầu và điểm cuối, cho phép giá trị này được sử dụng làm một đặc trưng của trường (vì nó chỉ phụ thuộc vào các điểm đã chọn của trường!). Như vậy, một đặc trưng khác của trường tĩnh điện, điện thế của nó, vừa được nêu ra. Trái với cường độ điện trường, điện thế này là một đại lượng vô hướng vì nó được biểu diễn theo công thực hiện.
HS B: Chúng em đã được học ở trường trung học cơ sở rằng khái niệm thế của một trường là không có ý nghĩa vật lí. Chỉ có độ chênh lệch thế của hai điểm bất kì của trường mới có ý nghĩa vật lí.
GV: Em nói khá đúng. Nói đại khái, phần thảo luận ở trên cho phép chúng ta xác định chính xác hiệu điện thế đó; hiệu điện thế giữa hai điểm a và b của điện trường (kí hiệu là φa - φb) được định nghĩa là tỉ số của công thực hiện bởi lực điện trường làm dịch chuyển điện tích q0 từ điểm a đến điểm b, và điện tích q0 đó, tức là

Như vậy, điện thế của điện trường tại một điểm cho trước có thể được xác định theo công thực hiện bởi lực điện trường làm dịch chuyển một điện tích đơn vị dương từ điểm cho trước đó đến vô cùng. Nếu công đang xét không do điện trường thực hiện, mà chống lại lực điện trường, thì thế tại một điểm đã cho là công phải thực hiện để làm dịch chuyển một điện tích đơn vị dương từ vô cùng đến điểm đã cho đó. Như vậy, định nghĩa này loại trừ phép đo thực nghiệm của điện thế tại một điểm của điện trường, vì trong thí nghiệm chúng ta không thể nào lùi ra xa vô cùng được. Chính vì lí do này mà người ta nói rằng hiệu điện thế của hai điểm trong điện trường mới có ý nghĩa vật lí, còn bản thân điện thế tại một điểm nào đó thì không. Chúng ta có thể nói rằng điện thế tại một điểm đã cho được xác định với độ chính xác đến một hằng số tùy ý. Giá trị của điện thế tại vô cùng thường được chọn làm hằng số này. Điện thế được đo tính từ giá trị này. Để cho tiện, người ta giả sử điện thế tại vô cùng là bằng không.
Trong khuôn khổ những giả định này, điện thế của một điện trường, gây ra bởi một điện tích điểm q1, đo tại một điểm cách điện tích đó một khoảng r, bằng

Trong tổng này, điện thế do điện tích dương gây ra có dấu cộng và điện thế do điện tích âm gây ra có dấu trừ.
GV: Khá chính xác. Bây giờ chúng ta xét khái niệm mặt đẳng thế. Quỹ tích của những điểm thuộc một điện trường có điện thế bằng nhau được gọi là một mặt đẳng thế (hay mặt thế không đổi). Có một đường sức và một mặt đẳng thế đi qua mỗi điểm trong một điện trường. Hỏi chúng định hướng với nhau như thế nào?
HS B: Em biết là tại mỗi điểm đường sức và mặt đẳng thế vuông góc với nhau.
GV: Em có thể chứng minh điều đó không?
HS B: Không, em không thể chứng minh.
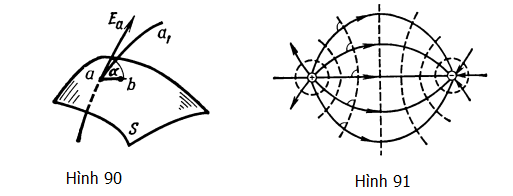

Trong số thừa số ở vế trái của phương trình (138), chỉ có cosα có khả năng bằng không. Vì thế, ta kết luận rằng α = 90o. Tôi nghĩ các em đã thấy rõ được rằng kết quả này thu được từ những chiều chuyển động ab khác nhau, biết rằng những chuyển động này nằm trong giới hạn của mặt đẳng thế S. Sự cong của mặt đẳng thế không ảnh hưởng đến lập luận của chúng ta bởi vì độ dời Dl là rất nhỏ.
Ngoài các đường sức ra, người ta còn dùng tiết diện của mặt đẳng thế để miêu tả một trường tĩnh điện trên phương diện hình học. Xét đến thực tế các đường sức và mặt đẳng thế này vuông góc với nhau, người ta có thể vẽ một họ tiết diện của mặt đẳng thế từ một họ đường sức đã biết, và ngược lại.
(Nói với HS A) Em hãy thử vẽ tiết diện của các mặt đẳng thế cho trường hợp ở Hình 88a? Để tránh nhầm lẫn chúng với đường sức, em hãy vẽ tiết diện của các mặt đẳng thế bằng đường đứt nét.
HS A: Em sẽ vẽ các đường đứt nét sao cho chúng luôn luôn giao vuông góc với các đường sức. Đây là hình vẽ của em (Hình 91).
GV: Hình vẽ của em là đúng.
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>