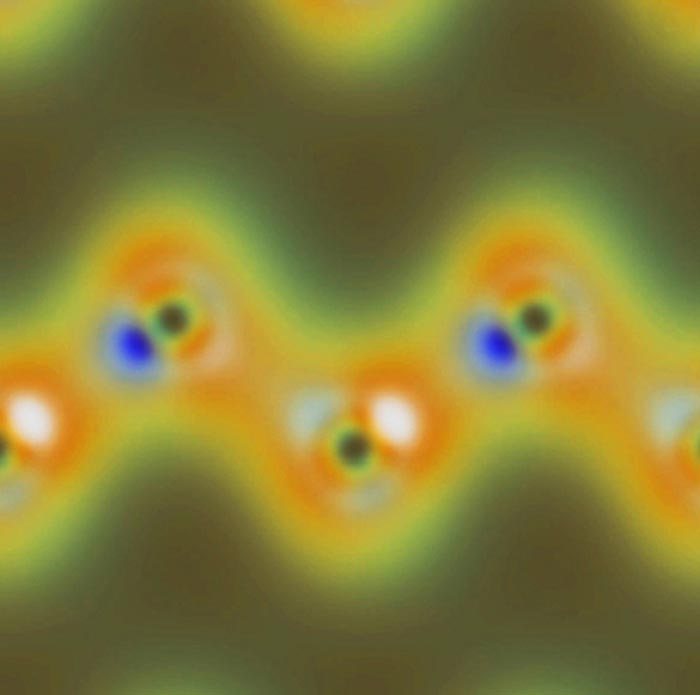
Một đóa hồng mới chớm nở trong mảnh vườn toán học: một sơ đồ Venn dạng hoa cho 11 tập hợp đối tượng.
Các sơ đồ Venn sử dụng những vòng tròn xen lấn để thể hiện tất cả những mối liên hệ có thể có giữa các tập hợp. Nhưng các sơ đồ cho nhiều hơn hai hoặc ba tập hợp thường đòi hỏi các vòng tròn phải kéo giãn ra, nén lại và xoay uốn để bao quát số lượng tăng dần các quan hệ tập hợp.
Những dạng hình học như vậy khiến nhà lôgic học người Anh John Venn cảm thấy khó chịu – ông là người đã sáng tạo ra những sơ đồ đó hồi những năm 1880. Ngoài ra, kết quả của sự nhào nặn toán học này có xu hướng quá phức tạp để khai thác cho mục đích có ích.
Cho nên, thay vậy, các nhà toán học đi tìm những sơ đồ đối xứng, chúng dễ hiểu hơn và đã được chứng minh là chỉ tồn tại cho những sơ đồ Venn có số lượng hoàn hảo các tập hợp. Vì mục đích minh bạch, những sơ đồ này cũng phải “đơn giản”, nghĩa là không có nhiều hơn hai đường cong cắt qua một điểm.
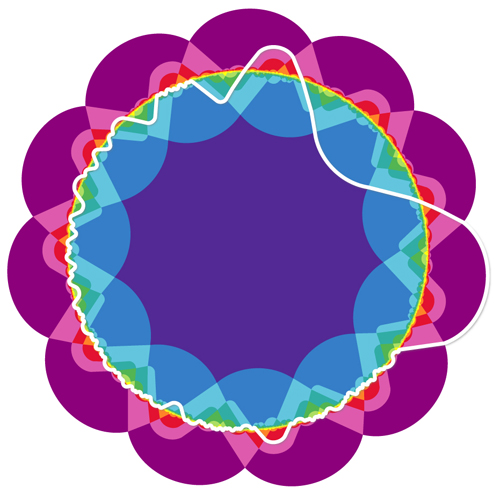
Sơ đồ Venn cho 11 tập hợp đối tượng. (Ảnh: Khalegh Mamakani và Frank Ruskey)
May mắn tình cờ
Trước đây, những ví dụ cho sơ đồ Venn đơn giản, đối xứng có năm và bảy tập hợp đã được tìm thấy – nhưng không có ví dụ cho số tập hợp cao hơn. Nay Khalegh Mamakani và Frank Ruskey tại trường Đại học Victoria ở British Columbia, Canada, vừa thành công trong việc thu được sơ đồ Venn 11 tập hợp đơn giản, đối xứng đầu tiên.
Một trong các tập hợp đó có đường bao màu trắng, và các màu sắc tương ứng với số lượng tập hợp chồng lấn. Đội nghiên cứu gọi sản phẩm sáng tạo của họ là Newroz, tiếng Kurd có nghĩa là “ngày mới”. Tên gọi đó cũng nghe tựa như “new rose” (đóa hồng mới) trong tiếng Anh, phản ánh diện mạo dạng bông hoa của sơ đồ.
Để tìm ra sơ đồ kiểu hoa hồng như trên, cặp đội nghiên cứu phải sàng lọc vô số sơ đồ khả dĩ, biểu diễn dưới dạng những danh sách số tương ứng với cách các đường cong cắt nhau. Duyệt qua hết mọi khả năng cho một sơ đồ 11 tập hợp sẽ là một nhiệm vụ không thể thực thi đối với các máy vi tính trên Trái đất, nên các nhà nghiên cứu đã thu hẹp các lựa chọn bằng cách ràng buộc tìm kiếm những sơ đồ có một tính chất gọi là đối xứng tắt chéo, nghĩa là một đoạn của mỗi tập hợp cắt qua tất cả những tập kia đúng một lần.
Nhà hình học trung kiên
Phương pháp giống như vậy đã được áp dụng để tìm những sơ đồ 7 tập hợp đơn giản, đối xứng. Tuy nhiên, các nhà nghiên cứu biết rằng không hề có sự đảm bảo sẽ thành công. “Sau khi tìm kiếm chúng khá lâu, bất ngờ lớn là rốt cuộc chỉ tìm thấy một,” Ruskey nói.
“Tôi thích hình vẽ đó,” phát biểu của Peter Cameron, một nhà toán học tại Queen Mary, Đại học London. Ông cho biết các kĩ thuật điện toán dùng để tìm ra Newroz có thể hữu ích trong việc biểu diễn những đối tượng hình học phức tạp khác.
Tuy nhiên, bản thân sơ đồ trên không có khả năng có những ứng dụng thực tiễn trực tiếp. “Chúng ta sử dụng các sơ đồ Venn hai và ba tập hợp để giải những câu đố lôgic đơn giản,” Cameron nói. “Ngoài ra, tôi không nghĩ ra người nào ngoài nhà hình học trung kiên nhất mới sử dụng sơ đồ Venn.”
Tham khảo: arxiv.org/abs/1207.6452
123physics (thuvienvatly.com)
Nguồn: New Scientist