Nhiệt động lực học căn bản - Phần 11

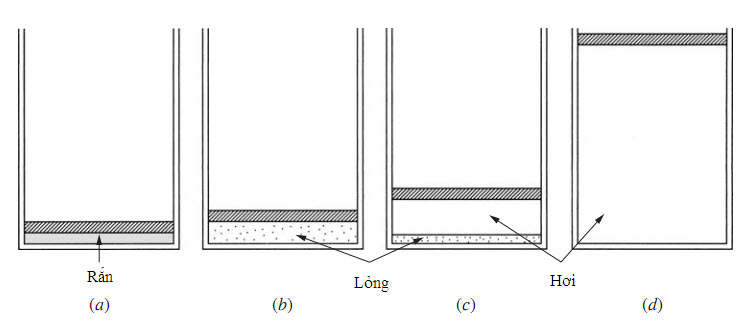
2.2 Vùng lỏng – hơi

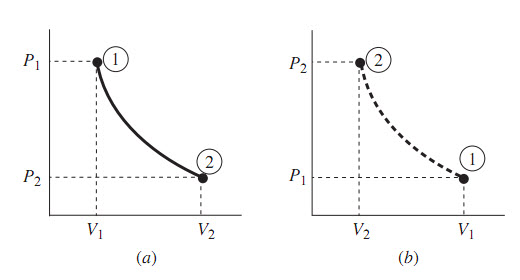
Tại trạng thái bất kì (T, υ) giữa hai điểm bão hòa f (trạng thái 1) và g (trạng thái 2), thể hiện trong Hình 2.4, chất lỏng và hơi phải tồn tại ở trạng thái cân bằng. Đặt υ_f và υ_g tương ứng là thể tích riêng của chất lỏng bão hòa và hơi bão hòa. Đặt m là tổng khối lượng của một hệ, m_f là khối lượng ở pha lỏng và m_g là khối lượng ở pha hơi. Khi đó, đối với một trạng thái của hệ biểu diễn bởi (T, υ) bất kì, ví dụ trạng thái 3, tổng thể tích của hỗn hợp bằng tổng thể tích chiếm giữ bởi chất lỏng và thể tích chiếm giữ bởi hơi, hay

υ = υ_f + υ_g          hoặc      mυ = m_fυ_f + m_gυ_g            (2.1)

Tỉ số giữa khối lượng hơi bão hòa và và tổng khối lượng được gọi là chất lượng của hỗn hợp, kí hiệu là x, và bằng

x = m_g / m                        (2.2)

Chúng ta thường gọi vùng nằm dưới các đường bão hòa là vùng chất lượng, hay vùng hỗn hợp, hay vùng ẩm; nó là vùng duy nhất nơi chất lượng x có nghĩa.

Biết rằng m = m_f + m_g, ta có thể viết phương trình (2.1), sử dụng định nghĩa của chúng ta về chất lượng, như sau

υ = υ_f + x (υ_g – υ_f )           (2.3)

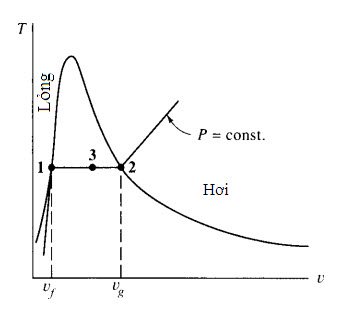
Hình 2.4 Đồ thị T-u thể hiện các điểm lỏng bão hòa và hơi bão hòa.

Do hiệu giá trị lỏng bão hòa và hơi bão hòa thường xuất hiện trong tính toán, nên ta đặt chỉ số dưới “fg” để kí hiệu hiệu này; nghĩa là

υ_fg = υ_g – υ_f                     (2.4)

Như vậy, phương trình (2.3) có thể viết là

υ = υ_f + xυ_fg                    (2.5)

Phần trăm chất lỏng tính theo khối lượng trong hỗn hợp là 100(1 – x), và phần trăm hơi là 100x.

Nhiệt động lực học căn bản
Merle C Potter
Bản dịch của Thuvienvatly.com

<< Phần trước | Phần tiếp theo >>