[SOLVED] Cho cơ hệ như hình vẽ, biết m1 = m2 = 400 g, k = 40 N/m

Câu hỏi

🗣️ Trần Khanh Thành hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

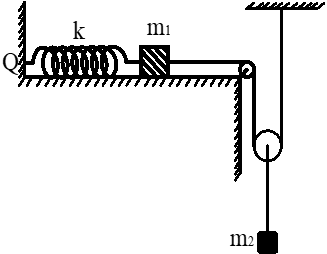
Cho cơ hệ như hình vẽ, biết m₁= m₂= 400 g, k = 40 N/m. Từ vị trí cân bằng, nâng vật m₂ theo phương thẳng đứng đến vị trí lò xo không biến dạng rồi thả nhẹ lúc t = 0. Bỏ qua mọi ma sát, sợi dây không dãn, khối lượng của dây và các ròng rọc không đáng kể; lấy g = 10 m/s². Biết vật m₁ dao động điều hoà với chu kỳ \[\frac{\pi }{{2\sqrt 5 }}s.\] Tại thời điểm \[t = \frac{{\sqrt 5 \pi }}{6}s\] thì lò xo kéo tường tường Q một lực có độ lớn

Cho cơ hệ như hình vẽ, biết m1 = m2 = 400 g, k = 40 N/m. Từ vị trí cân bằng (ảnh 1)

(A) 3 N.

(B) 2 N.

(D) 6 N.

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: ,2023, de thi thu vat li thi xa quang tri co dap an.

Câu trả lời hay nhất

🕵 Bạn Nguyễn Anh Dũng trả lời:

Chọn câu (A): 3 N.

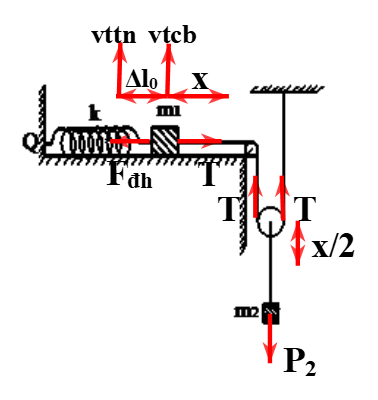
Tại vtcb thì ${m_2}g = 2T = 2k\Delta {l_0} \Rightarrow \Delta {l_0} = \frac{{{m_2}g}}{{2k}} = \frac{{0,4.10}}{{2.40}} = 0,05m = 5cm = A$ Khi vật m1 có li độ x thì \[\left\{ \begin{array}{l}T' - k\left( {\Delta {l_0} + x} \right) = - {m_1}{\omega ^2}x\\{m_2}g - 2T' = - {m_2}{\omega ^2}.\frac{x}{2}\end{array} \right.\] \[ \Rightarrow {m_2}g - 2k\left( {\Delta {l_0} + x} \right) = - {m_2}{\omega ^2}.\frac{x}{2} - 2{m_1}{\omega ^2}x\] \[ \Rightarrow \omega = \sqrt {\frac{{2k}}{{\frac{{{m_2}}}{2} + 2{m_1}}}} = \sqrt {\frac{{2.40}}{{\frac{{0,4}}{2} + 2.0,4}}} = 4\sqrt 5 \] (rad/s) $x = A\cos \left( {\omega t + \varphi } \right) = 0,05\cos \left( {4\sqrt 5 .\frac{{\sqrt 5 \pi }}{6} + \pi } \right) = 0,025m$${F_{dh}} = k\left( {\Delta {l_0} + x} \right) = 40.\left( {0,05 + 0,025} \right) = 3$ (N).

$Tại vtcb thì ${m_2}g = 2T = 2k\Delta {l_0} \Rightarrow \Delta {l_0} = \frac{{{m_2}g}}{{2k}} = \frac{{0,4.10}}{{2.40}} = 0,05m = 5cm = A$ Khi vật m1 có li độ x thì \[\left\{ \begin{array}{l}T$

Câu trước | Câu kế tiếp

Các câu trả lời

👤 Bùi Phương Đức viết:

Chọn C, 1 N.

👤 Đặng Gia Dũng viết:

Chọn D, 6 N.

👤 Trương Hải Thành viết:

Chọn B, 2 N.

👤 Phan Khánh Phú viết:

Chọn A, 3 N.

➥ 🗣️ Trần Khanh Thành trả lời: Cảm ơn bạn, câu này hình như có trong file doc này Đề+Đáp án thi thử Quốc gia, THPT Thị Xã Quảng Trị lần 2 năm 2017

👤 Nguyễn Trí Tân viết:

Chọn A: 3 N.

Gửi bạn các file hữu ích đi kèm câu hỏi:

Cho cơ hệ như hình vẽ, biết m1 = m2 = 400 g, k = 40 N/m. Từ vị trí cân bằng, nâng vật m2 theo phương thẳng đứng đến vị trí lò xo không biến dạng rồi

Câu hỏi

Câu trả lời hay nhất

Câu trước | Câu kế tiếp

Các câu trả lời

Sách Developing Skills For The Toeic Test

Sách Taking The TOEIC Skills and Strategies 1 (QR) First News

Làm thêm Trắc nghiệm ôn thi THPT

chọn đúng hoặc sai với mỗi ý a), b), c), d) Một khối khí đựng trong xilanh có pít-tông. Đốt nóng xilanh trong thời gian đủ dài (trong quá trình đốt

Một sợi dây đàn hồi dài 1,6 m với hai đầu cố định đang có sóng dừng. Biết tần số của sóng là 10" " Hz, tốc độ truyền sóng trên dây là 4 m/s. Số bụng và

Con lắc lò xo gồm lò xo có độ cứng k=20 N/m và vật nhỏ khối lượng m đang dao động cưỡng bức dưới tác dụng của ngoại lực F=5 cos⁡(10t) N (t tính bằng giây).

Sóng cơ trong đó các phần tử môi trường dao động theo phương vuông góc với phương truyền sóng được gọi là

Chiếu bức xạ tần số f vào tấm kim loại có công thoát A thì động năng cực đại của các quang electron thoát ra là K. Nếu bức xạ chiếu vào có tần số tăng

Một sợi dây AB dài 100 cm căng ngang, đầu B cố định, đầu A gắn với một nhánh của âm thoa dao động điều hòa với tần số 40 Hz. Trên dây AB có một sóng dừng