Henrik Melbéus và Tommy Ohlsson mô tả ba lí thuyết khác nhau của các chiều bổ sung, và làm thế nào có thể quan sát những chiều không nhìn thấy này, nếu như chúng thật sự có tồn tại.
Bức tranh vạn vật
Tóm lại, để trước nay không bị phát hiện ra, mọi chiều bổ sung đều phải thật nhỏ và đặc. Thật vậy, người ta có thể chất phác tưởng tượng rằng các chiều bổ sung phải nhỏ đến mức chúng ta sẽ không bao giờ có thể quan sát thấy chúng, ít nhất là trong tương lai trước mắt. Tuy nhiên, trong những năm gần đây, những mô hình khác nhau đã được đề xuất nhằm tránh những ràng buộc chặt chẽ như thế, cho phép các mô hình của các chiều bổ sung được kiểm tra trong các thí nghiệm vật lí hạt năng lượng cao.
Có ba mô hình chính mô tả các chiều không gian bổ sung. Trong kịch bản các chiều bổ sung vạn vật (mô hình UED), do các nhà vật lí lí thuyết Thomas Appelquist, Hsin-Chia Cheng và Bogdan Dobrescu đề xuất hồi năm 2001 (Phys. Rev. D 64 035002), tất cả các hạt thuộc Mô hình Chuẩn được phép truyền trong những chiều bổ sung đó, với mỗi hạt sơ cấp có tháp KK riêng của nó. Trong mô hình này, có một con số bổ sung (có thể sánh với khối lượng hay điện tích của một hạt) gắn với mỗi hạt gọi là “số chẵn lẻ KK”, nó được giả định là bảo toàn trong các phản ứng hạt, nghĩa là tích của các số chẵn lẻ KK của các hạt trước phản ứng phải bằng tích của các số chẵn lẻ KK của những hạt còn lại sau phản ứng. Số chẵn lẻ KK +1 được gán cho mọi hạt KK số chẵn, bao gồm tất cả các hạt Mô hình Chuẩn vì chúng có số KK bằng 0, còn những hạt KK số lẻ thì có số chẵn lẻ KK bằng – 1. Hệ quả của sự bảo toàn tính chẵn lẻ KK là những hạt KK số lẻ chỉ có thể sinh ra theo từng cặp, nó có xác suất xảy ra thấp mặc dù là chọn lựa duy nhất được phép. Hơn nữa, một hạt KK bậc hai (với số chẵn lẻ +1) có thể phân hủy thành hai hạt Mô hình Chuẩn – vì (+1) = (+1)(+1) – nhưng một hạt KK bậc một (với số chẵn lẻ – 1) không thể phân hủy thành bất kì số lượng nào của hạt Mô hình Chuẩn vì – 1 không bao giờ bằng (+1)n.
Mô hình UED sẽ phát sinh những hiệu ứng có thể quan sát tại LHC ví dụ như sự sinh ra của hai hạt Mô hình Chuẩn hoặc nhiều tín hiệu phức tạp hơn, như mô hình ADD mô tả dưới đây. Một gợi ý quan trọng khác của tính chẵn lẻ KK là nó đảm bảo cái gọi là hạt KK nhẹ nhất (LKP) là bền và do đó có thể là một ứng cử viên vật chất tối. Loại vật chất này được gọi là vật chất tối Kaluza–Klein.
Tiến lên chiều lớn
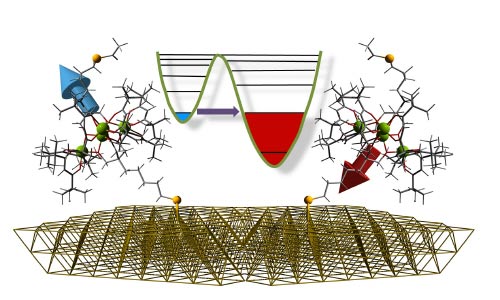
Mô hình quan trọng thứ hai mô tả “các chiều bổ sung lớn”, nó được đề xuất lần đầu tiên vào năm 1998 bởi Nima Arkani-Hamed, Savas Dimopoulos và Gia Dvali, trong cái gọi là mô hình ADD (Phys. Lett. B 429 263). Đặc điểm mới lạ của mô hình này là giả thuyết rằng các hạt Mô hình Chuẩn bị giam cầm một cái gọi là brane, nó được nhận ra với không-thời gian 4D bình thường, nhưng cư trú trong một không-thời gian lớn hơn (hình 2). Một sự tương tự là bề mặt của Trái đất là một lớp 2D cư trú trong một thời gian 3D lớn hơn. Trong trường hợp này, bề mặt Trái đất sẽ là brane.
Vì các hạt Mô hình Chuẩn chỉ “sống” trong các chiều thông thường, chứ không phải trong các chiều bổ sung, nên chúng sẽ không giúp chúng ta thiết lập giới hạn lên kích cỡ của các chiều bổ sung. Mặt khác, hạt trung chuyển lực hấp dẫn, graviton, không phải là một hạt Mô hình Chuẩn và do đó được phép truyền trong các chiều bổ sung. Trên nguyên tắc, giả thuyết lực hấp dẫn sóng trong một không-thời gian lớn hơn dẫn tới những sai lệch với điều kiện hấp dẫn Newton ở những cự li khoảng cách ngắn. Tuy nhiên, do tính yếu của nó so với những lực cơ bản khác, nên lực hấp dẫn chỉ mới được kiểm tra đến cỡ khoảng cách micron, và do đó các ràng buộc thực nghiệm vẫn còn khá yếu.
Không – thời gian cuộn
Ngoài mô hình ADD, các nhà vật lí lí thuyết Lisa Randall và Raman Sundrum còn đề xuất một mô hình tương tự vào năm 1999 (Phys. Rev. Lett. 83 4690). Đề xuất này được gọi tên chính thức là mô hình Randall–Sundrum (RS), nhưng thỉnh thoảng nó được gọi là lí thuyết hình học cuộn 5D, và nó giả rằng thế giới thực tế là một vũ trụ nhiều chiều hơn được mô tả bằng cơ sở hình học cuộn thay vì hình học phẳng như trong trường hợp mô hình ADD. (Hình học cuộn là hình học trong đó không gian bị uốn cong, giống như trong thuyết tương đối rộng Einstein.)
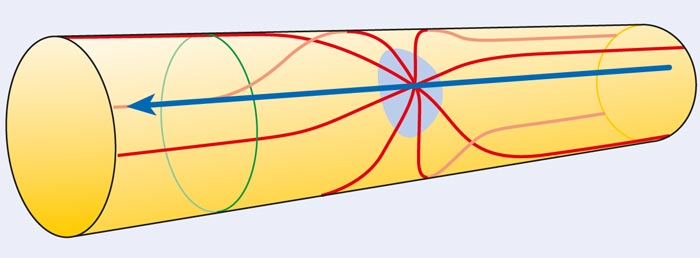
Hình 2. Mô hình ADD của các chiều bổ sung, tên đặt theo tên những người sáng tạo ra nó Nima Arkani-Hamed, Savas Dimopoulos và Gia Dvali, nó mô tả cái gọi là các chiều bổ sung lớn, theo đó các chiều bổ sung là lớn so với chiều dài Planck. Trong mô hình này, không-thời gian 4D của chúng ta (ba chiều không gian cộng với một chiều thời gian) là một lớp, hay một “brane”, tồn tại trong một không-thời gian nhiều chiều hơn. Tất cả các hạt Mô hình Chuẩn chỉ tồn tại trong brane của chúng ta, còn lực hấp dẫn thì vươn ra ngoài và đi vào thế giới nhiều chiều hơn đó. Một hệ quả của điều này là lực hấp dẫn sở dĩ yếu hơn những lực khác vì nó tác dụng xuyên qua các chiều bổ sung cũng như trong các chiều mà chúng ta có thể nhìn thấy. Hình vẽ này minh họa các đường sức hấp dẫn (màu đỏ) tạo ra bởi một khối lượng điểm trong một không gian có một chiều vô hạn (đường màu xanh đậm) và một chiều hữu hạn hay “bị cuộn lại” (vòng tròn màu xanh lục). Lực hấp dẫn chịu bởi một khối lượng điểm thứ hai tỉ lệ với số đường sức trên một đơn vị diện tích. Ở khoảng cách nhỏ hơn kích cỡ của chiều cuộn lại (đĩa màu xanh), các đường sức trải đều trong hai chiều, còn ở những khoảng cách lớn hơn các đường sức trở nên song song. Do đó, trong mô hình này, lực hấp dẫn là mạnh ở những khoảng cách rất nhỏ nhưng lại yếu ở một khoảng cách lớn.
Trong các mô hình ADD và RS, tính yếu của lực hấp dẫn so với những lực cơ bản khác liên quan đến dạng hình học của không-thời gian. Nói cho đơn giản thì lực hấp dẫn trải ra trong một không-thời gian lớn hơn so với những lực khác, chúng hỉ tác dụng trong brane 4D. Thật vậy, điều này có nghĩa là tất cả bốn lực cơ bản có thể có độ lớn bằng nhau và lực hấp dẫn chỉ có vẻ yếu hơn vì là một hệ quả của sự loãng hình học này.
Một khuôn khổ cuối cùng gợi ý đến các chiều bổ sung là lí thuyết dây, mặc dù lí thuyết này rất khác và mang tính giả thuyết cao hơn so với các lí thuyết KK tiêu biểu. Cách tiếp cận toán học này nỗ lực mô tả các hạt dưới dạng dao động của những sợi dây nhỏ xíu và dự đoán rằng số lượng chiều không-thời gian phải là 10 hoặc 11, tùy thuộc vào dạng thức chính xác của lí thuyết đó.
Cuộc săn tìm tiếp tục
Việc tìm kiếm các chiều bổ sung không phải chuyện của tương lai mà hiện đang diễn ra tại LHC. Nếu có tồn tại các chiều bổ sung, thì người ta có thể hi vọng tạo ra những hạt KK bằng cách cho va chạm những hạt bình thường (trong trường hợp LHC là proton) ở những năng lượng rất cao. Cho đến nay, cả ATLAS và CMS – hai thí nghiệm chính của LHC – đều không tìm thấy bất kì dấu hiệu nào của các chiều bổ sung. Tuy nhiên, những quan sát không thấy như vậy vẫn là có ích. Thực tế chẳng quan sát thấy gì đặt ra những ràng buộc mạnh hơn lên kích cỡ của các chiều bổ sung: nếu chúng tồn tại và cho đến nay chưa được nhìn thấy, thì đơn giản là vì chúng phải nhỏ hơn cái trước đây người ta nghĩ là cần thiết.

Máy dò hạt CMS (ảnh) và máy dò hạt ATLAS tại CERN đang tạo ra lượng dữ liệu đồ sộ giúp săn tìm các chiều bổ sung. (Ảnh: CERN)
Cho đến nay, những ràng buộc mới đã được đặt ra trên các mô hình ADD và RS bởi các thí nghiệm ATLAS và CMS. Đối với mô hình ADD, chúng tìm thấy cái gọi là cỡ Planck chiều bổ sung hiệu dụng, đó là mức năng lượng cao nhất có thể có mang lại ý nghĩa vật lí bên trong mô hình đã cho, phải lớn hơn 2 – 4 TeV, còn đối với mô hình RS, graviton cần nặng hơn 1 – 2 TeV. Vì cỡ năng lượng của một hạt KK, tức khối lượng của nó, về cơ bản tỉ lệ với nghịch đảo kích cỡ của chiều bổ sung, nên việc này tương đương với tìm một mức chiều dài tối đa cho chiều bổ sung đó.
Hôm 4 tháng 7 vừa qua, các nhóm hợp tác ATLAS và CMS tại CERN công bố rằng họ đã khám phá ra một hạt mới có khối lượng khoảng 125 GeV, có khả năng nhất đó là hạt Higgs danh tiếng. Nếu nó là hạt Higgs, thì kích cỡ đặc trưng của chiều bổ sung cần phải nhỏ hơn khoảng 1,8 x 10-18 m, khoảng bằng một phần một ngàn bán kính proton. Nhưng nên lưu ý rằng LHC thật ra chỉ mới bắt đầu thu thập dữ liệu, và vẫn còn nhiều cái để khám phá. Trước đây, những cỗ máy va chạm khác, kém mạnh hơn, đã được sử dụng để ràng buộc các chiều bổ sung theo một cách tương tự, đáng chú ý nhất là các máy gia tốc đã thành cựu như Máy va chạm Lớn Electron-Positron (LEP) tại CERN và Tevatron tại Fermilab ở Mĩ.
Các giới hạn trên các chiều bổ sung còn có thể nhận ra bởi nhiều thí nghiệm vật chất tối, ví dụ như máy dò XENON tại phòng thí nghiệm dưới lòng đất Gran Sasso ở Italy, các vệ tinh Fermi và PAMELA, và kính thiên văn neutrino IceCube tại Nam Cực. Thật vậy, trong năm nay nhóm hợp tác Fermi đã thiết lập những ràng buộc mạnh lên cỡ Planck trong mô hình ADD phù hợp với các kết quả LHC: nó phải lớn hơn 230 TeV cho hai chiều bổ sung, 16 TeV cho ba chiều, và 2,5 TeV cho bốn chiều. Nếu vật chất tối được cấu tạo từ những hạt KK – tức là vật chất tối Kaluza-Klein – thì những thí nghiệm này có thể hữu ích trong nghiên cứu các chiều bổ sung.
Mặc dù cả LHC lẫn các thí nghiệm vật chất tối cho đến nay đều không tìm thấy những dấu hiệu có sức thuyết phục của cơ sở vật lí vượt ngoài Mô hình Chuẩn, nhưng trong vài năm sắp tới LHC sẽ tạo ra lượng dữ liệu mới khổng lồ hi vọng sẽ cho biết các chiều bổ sung có tồn tại hay không. Chúng ta có thể biết câu trả lời đó trước khi hết năm nay. Cho dù chúng ta không biết đi nữa, thì những thí nghiệm khác sẽ tiếp tục tim kiếm, trong cái đang tỏ ra là một thời điểm rất hào hứng cho nghiên cứu vật lí ở mức độ cơ bản nhất của nó.
Henrik Melbéus là tiến sĩ vật lí lí thuyết, chuyên nghiên cứu các chiều bổ sung
Tommy Ohlsson là giáo sư vật lí lí thuyết, tác giả quyển giáo trình Vật lí Lượng tử Tương đối tính
Trần Nghiêm (thuvienvatly.com) dịch
Theo Physics World, tháng 9/2012