Ôn tập Vật Lý 10.
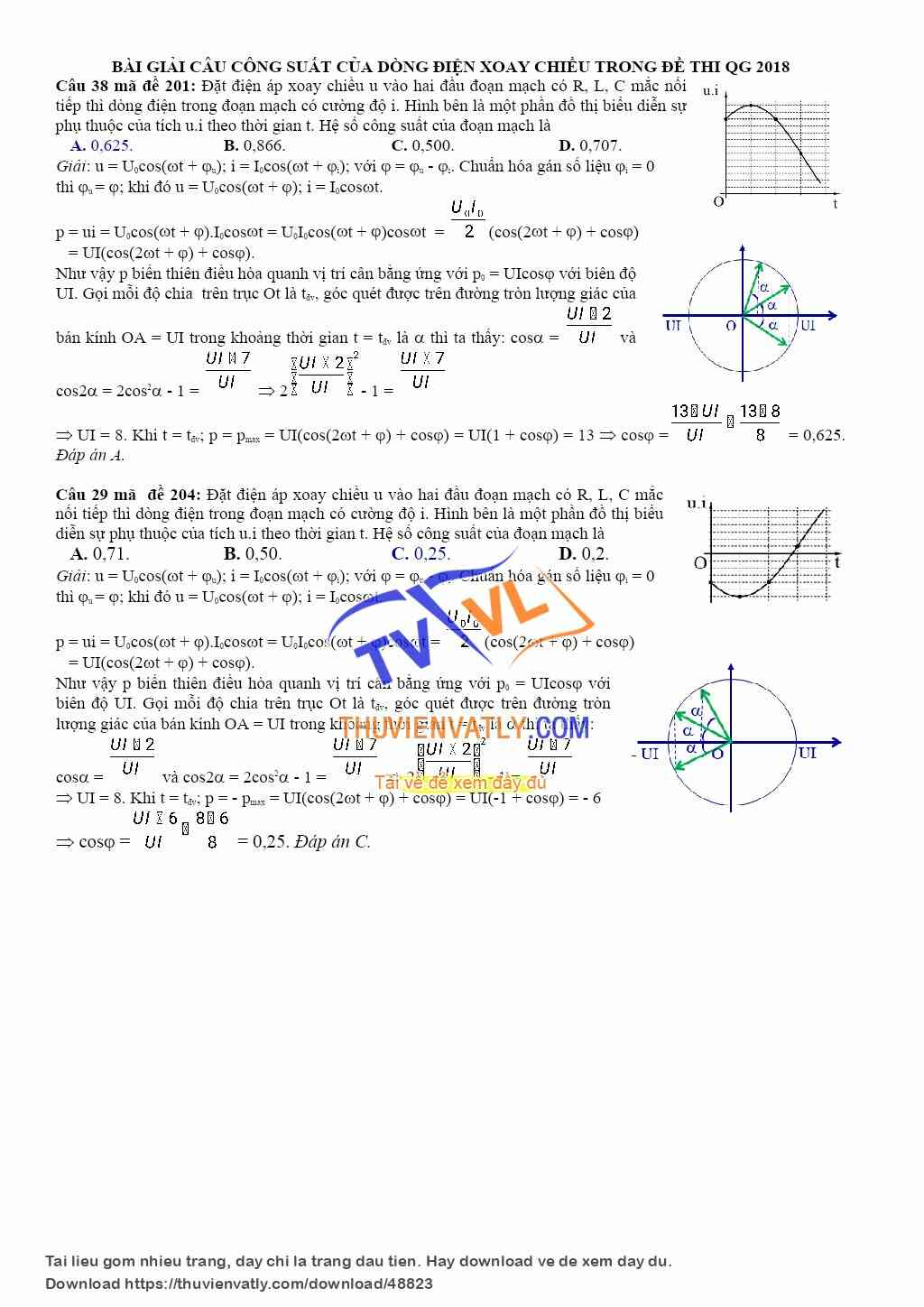
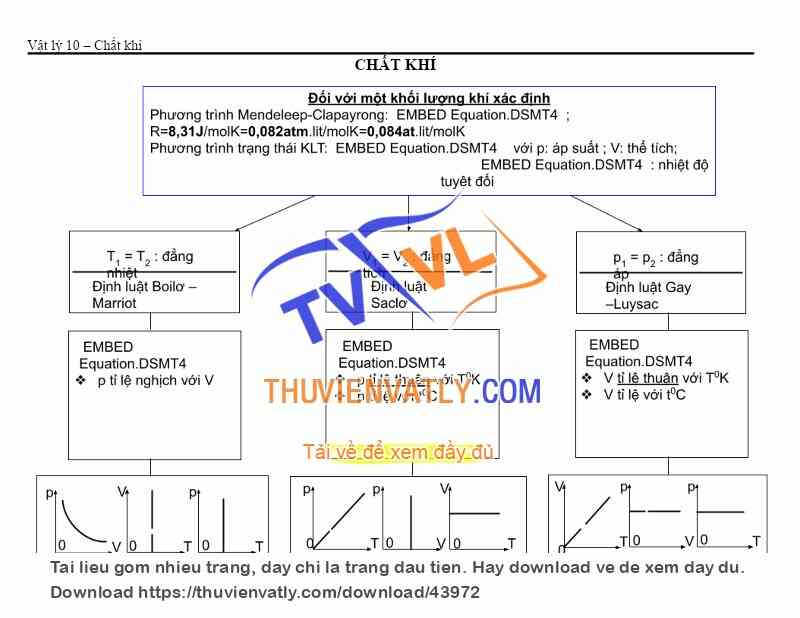
Sắp về hưu rồi, tặng bạn đọc của TVVL mấy cuốn sách mà mình cố công sưu tầm và biên soạn. Hay dở gì góp ý dùm nhé !
Để download tài liệu Ôn tập Vật Lý 10 các bạn click vào nút TẢI VỀ bên trên.
📁 Chuyên mục: Thư viện ôn tập kiến thức vật lý 10
📅 Ngày tải lên: 31/07/2014
📥 Tên file: sachontaply10cb.thuvienvatly.com.58d76.40529.docx (2.6 MB)
Thử sức các bài tập này nhé:
Câu 1:
Biết là độ dịch chuyển 10 m về phía đông còn là độ dịch chuyển 6 m về phía tây. Hãy xác định độ dịch chuyển tổng hợp .
- (A) 4 m về phía đông.
- (B) 4 m về phía tây.
- (C) 4 m về phía đông – bắc.
- (D) 4 m về phía tây – nam.
Câu 2:
Biết là độ dịch chuyển 3 m về phía đông còn là độ dịch chuyển 4 m về phía bắc. Hãy xác định độ lớn, phương và chiều của độ dịch chuyển tổng hợp .
- (A) d = 5 m có hướng đông - bắc 53°.
- (B) d = - 5 m có hướng đông - bắc 53°.
- (C) d = 7 m có hướng đông.
- (D) d = -7 m có hướng bắc
Câu 3:
Biết là độ dịch chuyển 10 m về phía đông còn là độ dịch chuyển 6 m về phía tây. Hãy xác định độ dịch chuyển tổng hợp .
- (A) 4 m về phía tây.
- (B) 8 m về phía tây.
- (C) 4 m về phía đông.
- (D) 8 m về phía đông.
