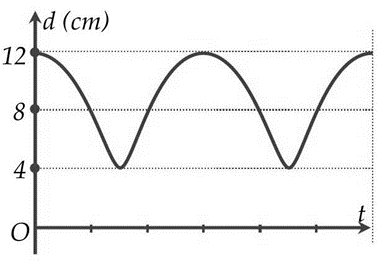
Hai vật nhỏ dao động điều hòa cùng tần số góc \(10{\rm{rad}}/{\rm{s}}\) , cùng biên độ trên hai đường thẳng vuông góc với nhau tại vị trí cân bằng

Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Trần Anh Đức hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập

(A) \(71,55{\rm{\;cm}}/{\rm{s}}\)

(B) \(58,79{\rm{\;cm}}/{\rm{s}}\)

(C) \(53,67{\rm{\;cm}}/{\rm{s}}\)

(D) \(78,38{\rm{\;cm}}/{\rm{s}}\)

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: ,2023, de thi thu vat li so nghe an ,lan 2, co dap an.

Câu trả lời hay nhất

🕵 Bạn Phạm Thị Lộc trả lời:

Chọn câu (A): \(71,55{\rm{\;cm}}/{\rm{s}}\)

\[{d^2} = x_1^2 + x_2^2 = {A^2}\left[ {{{\cos }^2}\left( {\omega t} \right) + {{\cos }^2}\left( {\omega t + \varphi } \right)} \right] = \] \[ = {A^2}\left[ {\frac{{2 + \cos \left( {2\omega t} \right) + \cos \left( {2\omega t + 2\varphi } \right)}}{2}} \right] = {A^2}\left[ {1 + \cos \varphi \cos \left( {2\omega t + \varphi } \right)} \right]\] \( \Rightarrow \left\{ \begin{array}{l}d_{\max }^2 = {A^2}\left( {1 + \left| {\cos \varphi } \right|} \right) = {12^2}\\d_{\min }^2 = {A^2}\left( {1 - \left| {\cos \varphi } \right|} \right) = {4^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left| {\cos \varphi } \right| = 0,8\\A = 4\sqrt 5 cm\end{array} \right.\) \({v_{\max }} = \omega A = 10.4\sqrt 5 = 40\sqrt 5 \) (cm/s) Khi một vật có \(a = 0 \Rightarrow v = {v_{\max }}\) thì vật còn lại có \(v = {v_{\max }}\left| {\cos \varphi } \right| = 40\sqrt 5 .0,8 \approx 71,55cm/s\) .

---

Câu trước | Câu kế tiếp

Các câu trả lời

👤 Đỗ Văn Minh viết:

Chọn C, \(53,67{\rm{\;cm}}/{\rm{s}}\)

---

👤 Ngô Văn Phúc viết:

Chọn D, \(78,38{\rm{\;cm}}/{\rm{s}}\)

---

👤 Đặng Văn Anh viết:

Chọn B, \(58,79{\rm{\;cm}}/{\rm{s}}\)

---

👤 Bùi Văn Phúc viết:

Chọn A, \(71,55{\rm{\;cm}}/{\rm{s}}\)

➥ 🗣️ Trần Anh Đức trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí Sở GD Nghệ An (Lần 1) có đáp án

---

👤 Nguyễn Phương Thành viết:

Chọn A: \(71,55{\rm{\;cm}}/{\rm{s}}\)

Gửi bạn các file hữu ích đi kèm câu hỏi:

• (2023) Đề thi thử Vật Lí Sở GD Nghệ An (Lần 1) có đáp án (.doc)
• (2023) Đề thi thử Vật Lí Sở GD Nghệ An (Lần 4) có đáp án (.doc)
• (2023) Đề thi thử Vật Lí Sở Nghệ An (Lần 2) có đáp án (.doc)
• (2023) Đề thi thử Vật Lí Sở Nghệ An (Lần 3) có đáp án (.doc)
• (2023) Đề thi thử Vật Lí THPT Yên Định 1 - Thanh Hóa (Lần 1) có đáp án (.doc)
• (2023) Đề thi thử Vật Lí THPT Nguyễn Khuyến Lần 2 có đáp án (.doc)
• Một trường hợp phản trực giác trong đó hai điện tích cùng dấu hút nhau
• Bài toán xác định thời gian trong dao động điều hòa