Câu hỏi
🗣️ Lê Diệp Kiệt hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
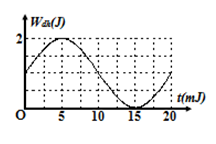
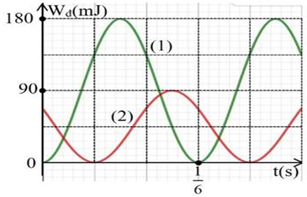
Hai vật nhỏ có cùng khối lượng \(100{\rm{\;g}}\) dao động điều hòa trên hai đường thẳng song song với nhau, cách nhau \(10{\rm{\;cm}}\), vị trí cân bằng của hai vật cùng nằm trên đường vuông góc với hai quỹ đạo. Hình vẽ bên là đồ thị biểu diễn động năng của mỗi vật theo thời gian. Tại thời điểm mà li độ của vật thứ nhất đạt cực đại thì khoảng cách giữa hai vật gần nhất với giá trị nào sau đây?
(A) \(13{\rm{\;cm}}\) .
(B) \(12{\rm{\;cm}}\) .
(C) \(14{\rm{\;cm}}\) .
(D) \(11{\rm{\;cm}}\) ,
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li so gd nghe an co dap an.
Câu trả lời hay nhất
🕵 Bạn Trần Văn Phúc trả lời:
Chọn câu (C): \(14{\rm{\;cm}}\) .
\(\frac{T}{2} = \frac{1}{6}s \Rightarrow T = \frac{1}{3}s \to \omega = \frac{{2\pi }}{T} = 6\pi \) (rad/s) \(k = m{\omega ^2} = 0,1.{\left( {6\pi } \right)^2} = 36\) (N/m) \({W_1} = \frac{1}{2}kA_1^2 \Rightarrow 0,18 = \frac{1}{2}.36.A_1^2 \Rightarrow {A_1} = 0,1m = 10cm\) \({W_2} = \frac{1}{2}kA_2^2 \Rightarrow 0,09 = \frac{1}{2}.36.A_2^2 \Rightarrow {A_2} = 0,05\sqrt 2 m = 5\sqrt 2 cm\) Tại \(t = \frac{1}{{18}}s = \frac{T}{6}\) thì \({W_{d2}} = 0 \Rightarrow \left| {{x_2}} \right| = {A_2} \to \) tại \(t = 0\) thì \[\left| {{x_2}} \right| = \frac{{{A_2}}}{2} = \frac{{5\sqrt 2 }}{2}cm\] và \(\left| {{x_1}} \right| = {A_1} = 10cm\) \(d = \sqrt {{O_1}{O_2}^2 + {{\left( {{x_1} - {x_2}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {10 \pm \frac{{5\sqrt 2 }}{2}} \right)}^2}} \Rightarrow \left[ \begin{array}{l}d \approx 16,8cm\\d \approx 11,9cm\end{array} \right.\) . hoặc C
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Trần Thị Dũng viết:
Chọn C, \(14{\rm{\;cm}}\) .
➥ 🗣️ Lê Diệp Kiệt trả lời: Cảm ơn bạn, câu này hình như có trong file pdf này Đề và đáp án thi thử ĐH Vật Lí LQĐ năm 2012
👤 Lê Thị Lộc viết:
Chọn D, \(11{\rm{\;cm}}\) ,
👤 Phạm Thị Đức viết:
Chọn B, \(12{\rm{\;cm}}\) .
👤 Lê Thị Thành viết:
Chọn A, \(13{\rm{\;cm}}\) .
👤 Đặng Văn Minh viết:
Chọn C: \(14{\rm{\;cm}}\) .
Gửi bạn các file hữu ích đi kèm câu hỏi:
- Đề và đáp án thi thử ĐH Vật Lí LQĐ năm 2012 (.pdf)
- Đáp án thi thử lần 2 diễn đàn vật lí phổ thông (.pdf)
- Đáp án Thi thử Đại học lần I 2013 của diễn đàn Vật lí phổ thông (.pdf)
- Đề và đáp án chi tiết thi thử ĐH Vật Lí trên tạp chí Vật Lí & Tuổi trẻ số ra tháng 1/2012 (.pdf)
- Đề thi thử Vật lí lần 8 - ĐHSP Hà Nội 2012 (Có đáp án) (.pdf)
- Đề và đáp án chi tiết thi thử ĐH Vật Lí trên tạp chí Vật Lí & Tuổi trẻ số ra tháng 2/2012 (.pdf)
- Chuyên đề: Giao thoa sóng với hai nguồn lệch pha nhau
- Điều kiện về khoảng cách giữa hai nguồn trong giao thoa sóng cơ
