Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.
Câu hỏi
🗣️ Trần Phan Bảo hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
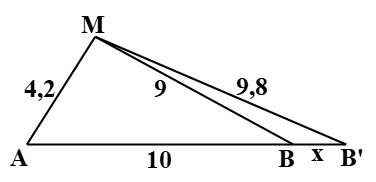
Hai nguồn phát sóng kết hợp A, B trên mặt nước cách nhau \(10{\rm{\;cm}}\) dao động theo phương trình \({u_1} = {u_2} = 2{\rm{cos}}40\pi t\;\left( {{\rm{cm}}} \right)\). Xét điểm \({\rm{M}}\) trên mặt nước cách \({\rm{A}},{\rm{B}}\) sao cho \({\rm{MA}} = 4,2{\rm{\;cm}}\) và \({\rm{MB}} = 9{\rm{\;cm}}\). Coi biên độ sóng không đổi và tốc độ truyền sóng trên mặt nước là \({\rm{v}} = 32{\rm{\;cm}}/{\rm{s}}\). Giữ nguyên tần số \(f\) và các vị trí \(A,M\). Cân dịch chuyển nguồn \(B\) xa nguồn \(A\) (dọc theo phương \(AB)\) một đoạn nhỏ nhất bao nhiêu để tại \(M\) là một cực tiểu giao thoa?
(A) \(8,74{\rm{\;mm}}\)
(B) \(7,27{\rm{\;mm}}\)
(C) \(8,16{\rm{\;mm}}\)
(D) \(7,47{\rm{\;mm}}\)
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li cum hai duong co dap an.
Câu trả lời hay nhất
🕵 Bạn Nguyễn Khánh Công trả lời:
Chọn câu (A): \(8,74{\rm{\;mm}}\)
\(\lambda = v.\frac{{2\pi }}{\omega } = 32.\frac{{2\pi }}{{40\pi }} = 1,6\) (cm) Ban đầu \({k_M} = \frac{{MB - MA}}{\lambda } = \frac{{9 - 4,2}}{{1,6}} = 3\) Lúc sau MB tăng thì \({k_M} = \frac{{MB' - 4,2}}{{1,6}} = 3,5 \Rightarrow MB' = 9,8\) \(\cos \widehat {MBA} + \cos \widehat {MBB'} = 0 \Rightarrow \frac{{{{10}^2} + {9^2} - 4,{2^2}}}{{2.10.9}} + \frac{{{x^2} + {9^2} - 9,{8^2}}}{{2x.9}} = 0 \Rightarrow x \approx 0,874cm = 8,74mm\)
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Phạm Hậu Anh viết:
Chọn C, \(8,16{\rm{\;mm}}\)
👤 Trần Khanh Minh viết:
Chọn D, \(7,47{\rm{\;mm}}\)
👤 Lê Trọng Phúc viết:
Chọn B, \(7,27{\rm{\;mm}}\)
👤 Trần Trí Minh viết:
Chọn A, \(8,74{\rm{\;mm}}\)
➥ 🗣️ Trần Phan Bảo trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí Cụm Hải Dương có đáp án
👤 Ngô Thị Phú viết:
Chọn A: \(8,74{\rm{\;mm}}\)
Gửi bạn các file hữu ích đi kèm câu hỏi:
- (2023) Đề thi thử Vật Lí Cụm Hải Dương có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Trịnh Hoài Đức - Bình Dương có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Lý Thường Kiệt - Hải Phòng (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Cụm Nam Định có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở GD Bình Dương (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Dĩ An - Bình Dương (Lần 1) có đáp án (.doc)
- Điều kiện về khoảng cách giữa hai nguồn trong giao thoa sóng cơ
- Bài giảng Dao động và Sóng (Phần 10)
