Câu hỏi
🗣️ Phạm Thị Đức hỏi: Cho mình hỏi một câu Trắc nghiệm ôn thi THPT trong sách bài tập
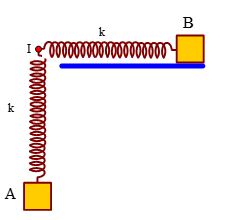
Đặt điện áp u = 40cos100πt (V) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp, trong đó cuộn cảm thuần có độ tự cảm L thay đổi được. Biết giá trị điện trở là 10 Ω và dung kháng của tụ điện là \(10\sqrt 3 \) Ω. Khi L = L1 thì điện áp giữa hai đầu cuộn cảm là
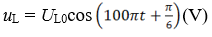 thì biểu thức cường độ dòng điện trong đoạn mạch là
thì biểu thức cường độ dòng điện trong đoạn mạch là(A) 
(B) 
(C) 
(D) 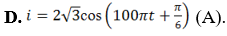
👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.
🔑 Chủ đề: ,2023, de thi thu vat li so nam dinh co dap an.
Câu trả lời hay nhất
🕵 Bạn Lê Trí Lộc trả lời:
Chọn câu (A): 
. Khi \[L = {L_1}\] thì: \[{\user2{\varphi }_{\user2{i1}}}\user2{ = }{\user2{\varphi }_{\user2{uL1}}}\user2{ - }\frac{\user2{\pi }}{\user2{2}}\user2{ = }\frac{\user2{\pi }}{\user2{6}}\user2{ - }\frac{\user2{\pi }}{\user2{2}}\user2{ = - }\frac{\user2{\pi }}{\user2{3}}\] điện áp u sớm pha hơn i 1 là π/3. \[\tan {\varphi _1} = \frac{{{Z_{L1}} - {Z_C}}}{R} = > \tan \frac{\pi }{3} = \frac{{{Z_{L1}} - 10\sqrt 3 }}{{10}} = > {Z_{L1}} = 20\sqrt 3 \Omega \] Khi \[L = {L_2} = \frac{2}{3}{L_1} = > {Z_{L2}} = \frac{2}{3}{Z_{L1}} = \frac{2}{3}20\sqrt 3 = \frac{{40}}{3}\sqrt 3 \Omega \] Dùng số phức: \[{i_\user2{2}}\user2{ = }\frac{u}{{R + ({Z_{L2}} - {Z_C})j}}\user2{ = }\frac{{40\angle 0}}{{10 + (\frac{{40\sqrt 3 }}{3} - 10\sqrt 3 )j}}\user2{ = 2}\sqrt[{}]{3}\angle - \frac{\pi }{6}\]
Câu trước | Câu kế tiếp
Các câu trả lời
👤 Trần Hải Hiếu viết:
Chọn C, 
👤 Lê Phương Nhân viết:
Chọn D, 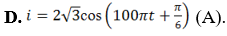
👤 Phạm Khánh Hoàng viết:
Chọn B, 
👤 Lê Minh Hưng viết:
Chọn A, 
➥ 🗣️ Phạm Thị Đức trả lời: Cảm ơn bạn, câu này hình như có trong file doc này (2023) Đề thi thử Vật Lí Cụm Nam Định có đáp án
👤 Lê Thế Thành viết:
Chọn A: 
Gửi bạn các file hữu ích đi kèm câu hỏi:
- (2023) Đề thi thử Vật Lí Cụm Nam Định có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở GD Nam Định (Lần 1) có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở GD Nam Trực - Nam Định có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở Nam Định có đáp án (.doc)
- (2023) Đề thi thử Vật Lí Sở GD Nam Định có đáp án (.doc)
- (2023) Đề thi thử Vật Lí THPT Nam Việt có đáp án (.doc)
- Lần đầu tiên chụp ảnh sự phân bố điện tích bên trong một phân tử
- Kính hiển vi điện tử nhiệt độ thấp lần đầu tiên ‘nhìn thấy’ các nguyên tử